Resumen
Se da una descripción de las leyes que se establecieron en una lista secuencial de todas las soluciones al problema de distribución de n-Queens. Se establece que:
- La proporción de soluciones completas en la lista general de todas las soluciones disminuye, con un valor creciente de n.
- Las soluciones completas se distribuyen en una lista secuencial de todas las soluciones de tal manera que es más probable que se encuentren soluciones completas ubicadas cerca una de la otra.
- Hay simetría en el orden de las soluciones completas en la lista general de todas las soluciones. Si en la posición i-ésima desde el comienzo de la lista la solución está completa, entonces la solución simétrica del final de la lista ubicada en la posición n-i + 1 también está completa (la regla de simetría de las soluciones).
- Cualquier par de soluciones, tanto cortas como completas, ubicadas simétricamente en la lista de todas las soluciones, son complementarias: la suma de los índices de posición de las líneas correspondientes es constante e igual a n + 1 (la regla de complementariedad de soluciones). Esto sugiere que solo la primera mitad de la lista de todas las soluciones completas es "única", cualquier solución completa de la segunda mitad de la lista se puede obtener sobre la base de la regla de complementariedad. Una consecuencia de esta regla es el hecho de que para cualquier valor de n, el número de soluciones completas siempre será un número par.
- La actividad de las celdas de las filas de la matriz de solución es simétrica con respecto al eje horizontal que pasa por el medio de esta matriz. Esto significa que la actividad de las celdas de la fila i-ésima siempre coincide con la actividad de las celdas de la fila n-i + 1. Por actividad se entiende la frecuencia con la que se produce el índice celular en la línea correspondiente de la lista de soluciones completas. De manera similar, la actividad de las celdas de las columnas de la matriz de la solución es simétrica con respecto al eje vertical que divide la matriz en dos partes iguales.
- Independientemente de n, en una búsqueda secuencial de todas las soluciones, la primera solución completa aparece solo después de una cierta secuencia de soluciones cortas. El tamaño de la secuencia inicial de soluciones cortas aumenta con n. La longitud de la lista de soluciones cortas antes de la aparición de la primera solución completa para valores pares de n es significativamente más larga que para los valores impares más cercanos.
- La línea en la matriz de decisión, en la cual las dificultades comienzan a avanzar, y se forma la primera decisión corta, divide la matriz de acuerdo con la regla de la proporción áurea. Para valores pequeños de n, tal conclusión es aproximada, sin embargo, con un aumento en el valor de n, la precisión de tal conclusión aumenta asintóticamente al nivel de la regla estándar.
Esta publicación presenta los principales resultados del artículo [1] , que fue publicado en la revista "Modeling of Artificial Intelligence, 2018, 5 (1)". En Habré hubo obras relacionadas con un problema de n-Queens: [2] , [3] ,
El problema de distribuir n reinas en un tablero de ajedrez de tamaño nxn tiene una larga historia. Originalmente fue formulado en 1848 por M. Bezzel [4] como una tarea intelectual para un tablero de ajedrez regular. Con el tiempo, el enunciado del problema fue ampliado por F. Nauck [5], y el tamaño de un tablero de ajedrez podría tener cualquier valor.
Introduccion
El enunciado del problema es bastante simple: necesita distribuir n reinas en un tablero de ajedrez de tamaño nxn para que en cada fila, cada columna y también en las diagonales izquierda y derecha que pasan por la celda donde se encuentra la reina, no haya más de una reina. Esta tarea es fácil de entender o explicar a alguien, pero es bastante difícil de resolver. El hecho es que no hay reglas en base a las cuales puede organizar reinas en cada línea para obtener una solución. Solo se puede obtener una solución enumerando varias variantes de la disposición de las reinas en ciertas líneas. Sin embargo, la complejidad de este método de solución radica en el hecho de que el número de todas las variantes de la disposición de las reinas aumenta exponencialmente al aumentar n. Además, dar un paso adelante para colocar a la reina en la posición libre de una determinada línea conduce a un cambio en la lista de posiciones libres en las líneas restantes, y al regresar un paso atrás, para formar una rama de búsqueda, es necesario borrar los rastros de las acciones realizadas anteriormente.
Hay una gran cantidad de publicaciones relacionadas con varios aspectos para resolver el problema de n-Queens. Se pueden atribuir a varias áreas de investigación: la búsqueda de todas las soluciones completas para un valor dado del tamaño de un tablero de ajedrez (n), el desarrollo de un algoritmo rápido para encontrar una solución para diferentes valores de n, la solución del problema completo a una solución completa, una composición arbitraria de k reinas, preguntas la complejidad computacional de los cálculos algorítmicos, así como varias modificaciones de la formulación original del problema. Para familiarizarse con estas áreas, recomendaría publicaciones interesantes de B. Jordan, S. Brett [6] e IP Gent, C. Jefferson, P. Nightingale [7], que proporciona una descripción bastante detallada de varias áreas de investigación. De particular interés es la publicación en Internet [8] apoyada por Walter Costers, que fue preparada por un grupo de la Universiteit Leiden y contiene enlaces a 342 publicaciones relacionadas con el problema de las n-reinas (a diciembre de 2018).
Aunque el problema n-Queens ha permanecido activo durante más de 150 años, y durante este tiempo han aparecido una gran cantidad de publicaciones, no pude encontrar un trabajo que fuera relevante para la búsqueda de patrones en los resultados de la solución de este problema. La mayoría de los proyectos relacionados con la búsqueda de todas las soluciones probablemente no guardaron las soluciones encontradas y no vieron lo que estaba "dentro". Allí, en el establecimiento de tareas, había otros objetivos dominantes, y nuestros estimados colegas los alcanzaron. Sin embargo, remotamente, me pareció que la situación es similar a cuando una persona hierve huevos para el desayuno, pero no los come, sino que los tira, dejando solo la cantidad de huevos hervidos en su memoria. Siempre he estado seguro de que si los datos no son aleatorios, debería haber cierta regularidad en ellos, incluso si no podemos encontrar esta regularidad. Fue esta convicción la razón de la búsqueda de patrones en esta tarea.
Junto con el deseo de proporcionar a los miembros de la comunidad Habr información útil para pensar, me gustaría que los programadores talentosos, la mayoría de los cuales en Habr, presten más atención a una dirección de desarrollo como la simulación por computadora (Simulación Computacional). Como método de investigación, dicha "Matemática algorítmica" se utiliza en la "vanguardia" de muchas áreas: Inteligencia artificial, Ciencia del software, Ciencia de datos, ... y estoy seguro de que los problemas muy complejos e importantes para la aplicación práctica se resolverán sobre la base de las matemáticas algorítmicas de lo contrario
Definiciones
En lo sucesivo, denotaremos el tamaño del tablero de ajedrez con el símbolo n. Una solución se llamará completa si todas las n reinas se colocan consistentemente en un tablero de ajedrez. Todas las demás soluciones, cuando el número de reinas colocadas correctamente es menor que n, llamaremos soluciones cortas. Por la longitud de una solución, nos referimos al número (k) de reinas colocadas correctamente. El número de todas las soluciones, para un valor dado de n, se denotará por m. Como un análogo de un "tablero de ajedrez" de tamaño nx n., Consideraremos una "matriz de solución" de tamaño nx n.
Inicio
Para realizar un estudio, se desarrolló un algoritmo para buscar todas las soluciones para un valor arbitrario de n. No utilizamos la recursión estándar o el sistema habitual de bucles anidados. Para valores grandes de n, este enfoque sería bastante problemático. El algoritmo se creó sobre la base de un conjunto de eventos que interactúan, en cada uno de los cuales se lleva a cabo un cierto sistema de acciones, interconectado. Esto hace posible implementar simplemente el mecanismo para cambiar el espacio de estado al elegir el siguiente nodo en la rama de la solución del problema (seguimiento hacia adelante), o borrar los rastros de acciones realizadas anteriormente, al regresar uno o más pasos (seguimiento hacia atrás). No hay requisitos especiales para el tamaño de la memoria o la velocidad del procesador en el algoritmo.
En base a este algoritmo, se encontraron todas las soluciones secuenciales (tanto cortas como completas) para varios valores de la matriz de solución n = (7, ..., 16). Dado que el tamaño de la lista de soluciones completas es la secuencia nombrada La enciclopedia en línea de secuencias enteras (secuencia A000170 [9]) y se indica en muchas publicaciones, me parece interesante enumerar el tamaño de la lista de todas las soluciones (cortas + completas) para los valores de n considerados por nosotros: 7 (194), 8 (736), 9 (2 936), 10 (12 774), 11 (61 076), 12 (314 730), 13 (1 716 652), 14 (10 030 692), 15 ( 62 518 772), 16 (415 515 376).
Además, utilizando las soluciones encontradas, damos la redacción de algunos problemas, métodos para resolverlos y una descripción de los resultados.
1. El espacio de estado en el que se buscan soluciones
La enumeración de varias opciones para la disposición de reinas en ciertas filas de una matriz de una decisión de tamaño n conduce a la formación de un espacio de estado. Si no hubiera prohibiciones en la disposición de las reinas en una u otra celda de la matriz, entonces el tamaño del espacio de estado sería n n . Si tomamos en cuenta solo la regla que prohíbe la ubicación de más de una reina en cada fila y cada columna, entonces obtenemos un subconjunto del espacio de estado, ¡cuyo tamaño será igual a n! Este subconjunto del espacio de estados corresponde al problema de la distribución de n por la torre. Si, junto con esto, también tenemos en cuenta la regla que prohíbe la ubicación de más de una reina en las diagonales izquierda y derecha que pasan a través de la celda donde se encuentra la reina, ¡entonces obtenemos un espacio de búsqueda cuyo tamaño será menor que n! .. Llamamos a ese subconjunto del espacio de estado - un espacio de búsqueda productivo, basado en el hecho de que solo en este subespacio se encuentran todas las soluciones posibles. Cualquier rama completada en el espacio de búsqueda productiva son soluciones con un cierto número de reinas colocadas correctamente. Básicamente, estas son decisiones cortas, y solo una pequeña parte restante son decisiones completas.
La Figura 1 muestra gráficos del logaritmo natural de tres indicadores: a) el valor factorial (n!) Sobre el tamaño de la matriz de decisión; b) el número de todas las decisiones (tanto cortas como completas); c) el número de soluciones completas, dependiendo del tamaño de la matriz de soluciones (n). Como se esperaba, todas las curvas se caracterizan por un aumento exponencial con el aumento de n. Las tasas de crecimiento del número de todas las soluciones y el número de soluciones completas difieren, aunque esto no es tan notable en el gráfico, debido al pequeño tamaño de la muestra de n valores. Por ejemplo, para n = 13, la diferencia entre los logaritmos de estos indicadores es 3.148, y para n = 16 esta diferencia aumenta en 0.190 y es 3.338. Obviamente, con un aumento adicional en n, esta discrepancia será más significativa.

Fig. 1 Dependencia del logaritmo del tamaño del espacio de estado en el valor n
2. ¿Cómo cambia la proporción de decisiones completas en la lista general de todas las decisiones?
Obviamente, si la tasa de crecimiento del número de soluciones completas va a la zaga del índice de crecimiento del número de todas las soluciones, entonces la probabilidad de encontrar una solución completa en la lista general de todas las soluciones disminuirá al aumentar n. La Figura 2 muestra un gráfico de la proporción de soluciones completas en la lista general de todas las soluciones en el valor de n. Se ve que con un aumento en el tamaño de la matriz de soluciones, la proporción de todas las soluciones completas en la lista general disminuye. Para los valores iniciales n = (7, ..., 14), este valor disminuye 5,66 veces desde el valor 0,2062 a 0,0364, y luego continúa una disminución gradual y asintótica de este valor. Aquí surge una contradicción formal entre las dos afirmaciones: por un lado, el número de soluciones completas aumenta exponencialmente al aumentar n, y por otro, la probabilidad de obtener una solución completa en una lista secuencial de todas las soluciones está disminuyendo constantemente. Esta aparente paradoja se explica de manera muy simple, el tamaño del espacio productivo y el tamaño asociado de la lista de todas las soluciones crece más rápido al aumentar n que el número de soluciones completas. Esto es como tratar de encontrar una aguja en un pajar: la cantidad de heno "al aumentar n" crece más rápido que la cantidad de agujas que se pierden allí. Por lo tanto, podemos suponer que si, para n = 27, el número de soluciones completas es aproximadamente 2.346 * 10 17 , entonces el valor correspondiente del número de todas las soluciones probablemente sea 3-4 órdenes de magnitud mayor que ~ 10 20
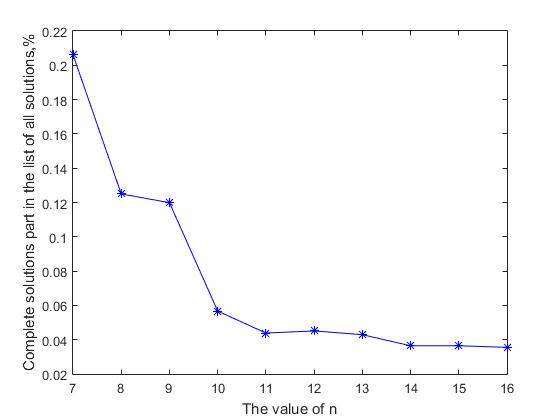
Fig. 2 Disminución de la proporción de soluciones completas en la lista general de todas las soluciones con n creciente
3. ¿Cuál es la frecuencia de soluciones de varias longitudes en la lista de todas las soluciones?
Como se mencionó anteriormente, todas las ramas completadas en el espacio de búsqueda productiva son soluciones con un número diferente de reinas colocadas correctamente.
Nos interesa con qué frecuencia hay soluciones de varias longitudes en la lista general de todas las soluciones.
La Tabla 1 para los valores n = (7, ..., 12) presenta los valores correspondientes de las frecuencias relativas para soluciones que tienen diferentes longitudes. La representación visual correspondiente de estos datos se muestra en la Figura 3.
El análisis de la tabla nos permite sacar las siguientes conclusiones:
a) para cada matriz de tamaño n, hay una cierta longitud de la solución que tiene una frecuencia máxima (resaltada en negrita).
Tabla 1. Frecuencia relativa (%) de soluciones de diferentes longitudes (k) para una matriz de tamaño n = (7, ..., 12)
| n \ k | 4 4 | 5 5 | 6 6 | 7 7 | 8 | 9 9 | 10 | 11 | 12 |
|---|
| 7 7 | 10,31 | 31,23 | 27,84 | 20,62 | | | | | |
| 8 | 2,45 | 20,38 | 34,78 | 29,89 | 12,50 | | | | |
| 9 9 | 0,34 | 5,79 | 21,73 | 35,83 | 34,32 | 11,99 | | | |
| 10 | 0,05 | 1,35 | 8.41 | 25,62 | 32,94 | 25,96 | 5,67 | | |
| 11 | | 0,15 | 2.12 | 11.80 | 26,71 | 34,47 | 20,36 | 4.39 | |
| 12 | | 0,01 | 0,29 | 3.28 | 13,56 | 29,88 | 31,29 | 17,18 | 4.51 |
b) a medida que aumenta n, aumenta el número de soluciones con diferentes longitudes. En consecuencia, la frecuencia relativa de todas las decisiones disminuye.
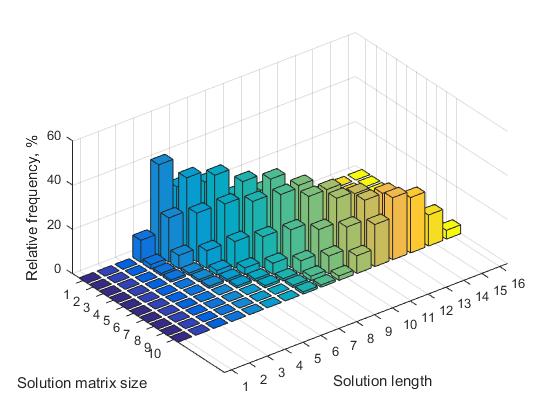
Fig. 3 Frecuencia de soluciones de varias longitudes dependiendo del tamaño de la matriz de solución, n = 7, ..., 16
c) para cada matriz de tamaño n, hay un cierto tamaño mínimo de la longitud de la solución, por debajo del cual no se producen soluciones cortas. Con el aumento de n, el valor de este umbral aumenta. Por ejemplo, para n = 8, el valor umbral es 4, respectivamente, para n = 16, el valor umbral es 7.
4. ¿Cuál es la disposición relativa de las soluciones completas en una lista secuencial de todas las soluciones?
En el enunciado del problema "sobre la distribución de n reinas" no hay razones que den razones para hacer una suposición sobre la secuencia de decisiones completas en la lista general de todas las soluciones. Estábamos interesados en saber si las soluciones completas en la lista general se distribuyen de manera uniforme, aleatoria o si tiene algunas peculiaridades. Para averiguarlo, analizamos las distancias entre las soluciones completas más cercanas en una lista secuencial de todas las soluciones. Como se puede ver en la Figura 4, donde para n = 12, se presenta un gráfico de cambios en las frecuencias correspondientes,
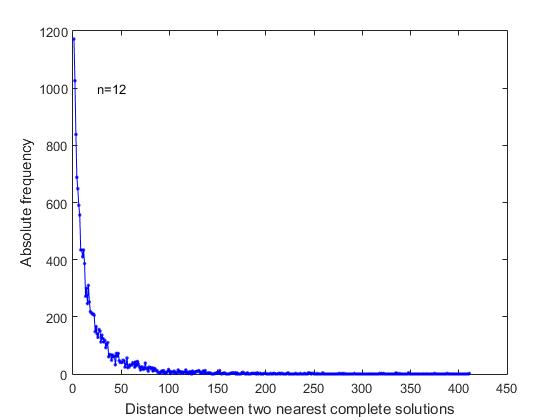
Fig. 4 Frecuencia versus distancia entre las soluciones completas más cercanas en una lista secuencial de todas las soluciones completas (n = 12)
Con la mayor frecuencia, existen soluciones completas que se suceden inmediatamente en una lista secuencial común de todas las soluciones. Estos son los casos de la formación de la rama de búsqueda cuando la relación de posiciones libres en las últimas líneas le permite formar dos o más soluciones completas consecutivas. Además, la frecuencia máxima son aquellas soluciones completas entre las que se encuentran: una solución corta, dos soluciones cortas, etc.
5. ¿Existe un patrón en la disposición de soluciones completas en la lista general de todas las soluciones?
Para responder a esta pregunta, hemos analizado listas secuenciales de todas las soluciones para los valores n = (7, ..., 16). Para demostrar claramente los resultados, en la Figura 5, para el valor n = 8, se presenta un gráfico donde se indica sucesivamente la longitud de cada solución en la lista de las 736 soluciones. Aquí, solo 92 soluciones están completas y están resaltadas en rojo, las 644 soluciones restantes son cortas y están resaltadas en azul. Se puede ver que las soluciones completas no se distribuyen uniformemente en la lista de todas las soluciones. Hay áreas donde las soluciones completas son más comunes, y hay lugares donde las soluciones completas son poco comunes o nada.

Fig. 5 La longitud de cada solución en una lista secuencial de todas las soluciones, para una matriz de 8 x 8 (rojo - soluciones completas, azul - soluciones cortas). El número total de todas las soluciones es 736
Sin embargo, algo más es importante aquí. Si observa cuidadosamente la imagen que se asemeja a un código de barras azul-rojo, notará una característica muy importante, todas las líneas rojas son simétricas con respecto a alguna línea vertical condicional que pasa por el medio de la lista de soluciones. , , i- , , m-i+1. , n=8, , 43- , , 736- 43 +1=694. 17- 10x10 368- , 12774-17+1=12407. . . n, , i- , , m-i+1 ( ). m, , . , n, , . ( – ).
, – . n+1 . , 17- n=10 368- (1, 5, 7, 10, 4, 2, 9, 3, 6, 8).
, 12407 (10, 6, 4, 1, 7, 9, 2, 8, 5, 3). , (11, 11, …,11). n, , , . . n, ( , ), , – n+1 ( ). Q(i ) Q1(i) – ,
<b>`Q ( i ) + Q1 ( i ) = n + 1, i = (1, n) `</b>
Esta regla significa que si se obtiene una solución completa en el i- ésimo paso, entonces se conoce la solución simétrica completa en el paso m - i +1. Por lo tanto, al buscar todas las soluciones completas, es suficiente encontrar solo la primera mitad de todas las soluciones completas. La segunda mitad de la lista de soluciones completas se puede determinar a partir de las soluciones ya obtenidas, en función de la regla de complementariedad. El criterio de que se alcance la mitad de la lista de soluciones completas es el cumplimiento de la regla de complementariedad entre la solución completa anterior Q (i-1) y la posterior Q (i) . es decir, es necesario que la suma de cada par de índices correspondientes de dos soluciones consecutivas sea igual a n + 1 . Dado que cualquier solución completa de la lista de todas las soluciones completas es única, solo aquellas soluciones completas consecutivas serán complementarias que estén a ambos lados del borde que divide la lista por la mitad.
Estas dos reglas permitirán en el futuro, al buscar todas las soluciones completas para cualquier valor siguiente de n, reducir la cantidad de cómputo y, en consecuencia, el tiempo de cálculo a la mitad.
6. Visualización de la secuencia de pasos para encontrar la primera solución completa.
¿Cómo es el proceso de realizar pasos hacia adelante (seguimiento hacia adelante) y regresar hacia atrás (seguimiento hacia atrás) al formar una rama de una búsqueda de solución? Para responder a esta pregunta, nosotros, para una matriz de 10 x 10, determinamos la secuencia de las 194 transiciones iniciales entre las líneas hasta que aparece la primera solución completa. El gráfico correspondiente se muestra en la Figura 6. Las líneas azules indican un movimiento hacia adelante, y las líneas rojas indican un retorno. Durante estos 194 pasos, se crearon 35 soluciones cortas. La figura muestra que la mayoría de las transiciones (84.5%) ocurren entre las líneas (5, 6, 7, 8). Este es un tipo de "cuello de botella" en el camino hacia la "meta". Como se desprende de la figura, solo hay 7 casos de cambio a la cuarta línea y un caso de cambio a la tercera línea. También hay 13 casos de cambio a la novena línea. Tres intentos de pasar a la línea 10 no tuvieron éxito, ya que en estas ramas de búsqueda en la línea 10 no había una posición vacía. Este ejemplo muestra todas las ramas de short

Fig. 6 Visualización de eventos Backtracking (rojo) y Forwardtracking (azul) para los primeros 194 pasos de búsqueda (n = 10)
soluciones, hasta la primera solución completa. Cualquier algoritmo para resolver dicho problema será efectivo si contiene un mecanismo que eliminará todas (o parte) de las ramas que conducen a soluciones cortas.
7. ¿Después de cuántas decisiones cortas aparece la primera solución completa?
Teniendo en cuenta que las soluciones completas aparecen de manera diferente en diferentes partes de la lista de todas las soluciones, parece importante averiguar en cuántas soluciones cortas aparece la primera solución completa cuando se buscan todas las soluciones de manera secuencial. Para este propósito, para los valores n = (7, ..., 35), todas las soluciones cortas se calcularon sucesivamente hasta la aparición de la primera solución completa. Como se puede ver en la Figura 7, que muestra un gráfico de la dependencia de n, el logaritmo natural del número de paso cuando apareció la primera solución completa, para valores pares de n, la primera solución completa aparece mucho más tarde que para los valores impares más cercanos de n. Por ejemplo, para un valor impar n = 21, la primera solución completa aparece en el paso 3138, y para el siguiente valor par n = 22, la primera solución completa aparece en el paso 628169. En consecuencia, para el siguiente valor impar n = 23, la primera solución completa aparece en el paso 9155.

Fig. 7 El número de soluciones cortas hasta la primera solución completa, para varios valores de n
El número de pasos de iteración para pares n = 22 es 200.2 y 68.6 veces más, respectivamente, que los valores impares más cercanos. Esto es especialmente evidente al contar el tiempo para n = 34. Aquí, la primera solución completa aparece en 826 337 184 pasos, y para los números impares más cercanos (33, 35), respectivamente, en 50 704 900 y 84 888 759 pasos. También se debe decir acerca de la violación del crecimiento monotónico del número de soluciones cortas antes de la aparición de la primera solución completa, con un aumento de n. Para valores pares de n, esto ocurre en n = 19, para valores impares, en n = 24 yn = 26.
8. ¿La frecuencia de celda de cada fila en la lista de todas las soluciones completas es la misma?
La matriz de decisión de tamaño nxn, que sirve como un análogo de un tablero de ajedrez, es como una escena en la que tienen lugar todos los eventos. Cualquier solución completa formada en esta escena consiste en índices de celdas de diferentes filas, porque cada una de esas celdas es un nodo en la rama de búsqueda de solución. La pregunta que nos interesará es la siguiente: ¿la carga en cada fila es la misma para diferentes celdas cuando se forma una lista de todas las soluciones completas? Obviamente, cuanto mayor es el valor de frecuencia, mayor es la actividad de esta celda para formar una lista de soluciones completas. Para establecer esto, determinamos para cada fila, en base a una lista de todas las soluciones completas, la frecuencia relativa de los diversos índices. Primero, analizamos una matriz de solución de tamaño n = 8. Examinemos cada fila del conjunto de soluciones completas secuencialmente y determinemos la frecuencia de varios valores de índice. La Tabla 2 muestra los valores correspondientes de las frecuencias absolutas de actividad de diferentes celdas en cada una de las ocho filas, y en la Fig. 8
Tabla 2. Frecuencia absoluta de actividad celular en cada una de las ocho filas de la matriz de decisión 8x8, basada en un análisis de la lista de todas las soluciones completas
| fila \ col | 1 | 2 | 3 | 4 4 | 5 5 | 6 6 | 7 7 | 8 |
|---|
| 1 | 4 4 | 8 | 16 | 18 años | 18 años | 16 | 8 | 4 4 |
| 2 | 8 | 16 | 14 | 8 | 8 | 14 | 16 | 8 |
| 3 | 16 | 14 | 4 4 | 12 | 12 | 4 4 | 14 | 16 |
| 4 4 | 18 años | 8 | 12 | 8 | 8 | 12 | 8 | 18 años |
| 5 5 | 18 años | 8 | 12 | 8 | 8 | 12 | 8 | 18 años |
| 6 6 | 16 | 14 | 4 4 | 12 | 12 | 4 4 | 14 | 16 |
| 7 7 | 8 | 16 | 14 | 8 | 8 | 14 | 16 | 8 |
| 8 | 4 4 | 8 | 16 | 18 años | 18 años | 16 | 8 | 4 4 |
Se presenta un grupo de 4 gráficos, donde cada gráfico caracteriza el cambio en las frecuencias relativas dentro de una línea. Una de las conclusiones fundamentalmente importantes que se pueden extraer del análisis de todos los datos obtenidos es la siguiente:
- para una matriz de decisión de tamaño arbitrario n , la actividad de las celdas de la fila i- ésima coincide con la actividad de la celda n-i + 1 , es decir la actividad de las celdas de la primera fila siempre coincide con la actividad de las celdas de la última fila, respectivamente, la actividad de las celdas de la segunda fila coincide con la actividad de las celdas de la penúltima fila, etc.
Si n es impar, solo la fila mediana de la matriz de solución no tiene un par simétrico; para todas las demás celdas, la regla anterior es válida - Llamamos a esto la "propiedad de simetría horizontal de la actividad de las celdas de diferentes filas de la matriz de solución" . Por esta razón, presentamos solo 4 gráficos para la matriz de decisión de tamaño n = 8, ya que los gráficos correspondientes de la actividad celular para las filas (1, 8), (2.7), (3.6) y (4.5) son completamente idénticos.
También se debe tener en cuenta que los valores de frecuencia son simétricos sobre el eje vertical que divide la matriz en dos partes iguales (en el caso de un valor par de n), o que pasan por la columna mediana (en el caso de un valor impar de n). Llamamos a esto la "propiedad de simetría vertical de la actividad de las celdas de diferentes filas de la matriz de solución" .
Además, como se deduce del análisis de la Tabla 2, las frecuencias en la matriz de la solución son simétricas con respecto a las diagonales principales izquierda y derecha.
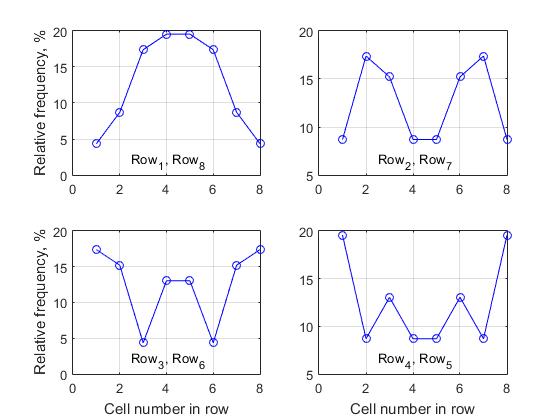
Fig. 8 Actividad celular de las filas correspondientes al formar la lista de soluciones completas, n = 8
Creo que la presencia de reglas restrictivas en el enunciado del problema y la propiedad relacionada del no determinismo, "forman" una especie de relación armoniosa entre nodos en diferentes líneas. Esas ramas de la búsqueda que se ajustan a estas reglas conducen a la formación de una solución completa. Las ramas restantes de la búsqueda, en algún momento, violan estas reglas y, como resultado, "completan su viaje" en forma de decisiones cortas. Cabe señalar aquí que las celdas de la matriz de decisión tienen solo una relación local dentro del grupo de influencia de proyección, no hay reglas prescritas para acciones coordinadas entre ellas. La actividad colectiva de las células es solo una consecuencia del resultado de la influencia de reglas restrictivas. Por lo tanto, queda abierta una pregunta bastante interesante: cómo las reglas restrictivas, como los factores de no determinismo, afectan las células de la matriz de decisión, lo que en última instancia conduce a la formación de una matriz de actividad celular "armoniosa", simétrica con respecto a los ejes horizontal y vertical, así como con respecto a la izquierda y diagonales principales derechas. ¿Es esta una propiedad característica de solo este problema, o también es válida para otros problemas no deterministas?
9. ¿Desde qué número de línea se activa el algoritmo de seguimiento de avance - retroceso?
Si seguimos la operación del algoritmo de selección de fila secuencial en la matriz de decisión para la ubicación de la reina, podemos ver que a partir de una determinada línea, que llamaremos "StopRow", el proceso de avanzar es "frenado". En la rama de búsqueda, esta es la primera línea donde hay problemas con la disponibilidad del servicio gratuito.

Fig. 9-1 Dependencia de la relación del índice StopRow con respecto al tamaño de la matriz de decisión (parte 1)
posición para la ubicación de la reina. Es a partir de esta línea que se activa el algoritmo de seguimiento Atrás para borrar los rastros de las acciones realizadas anteriormente y regresar. Esta es la línea en la que aparece la primera solución corta.
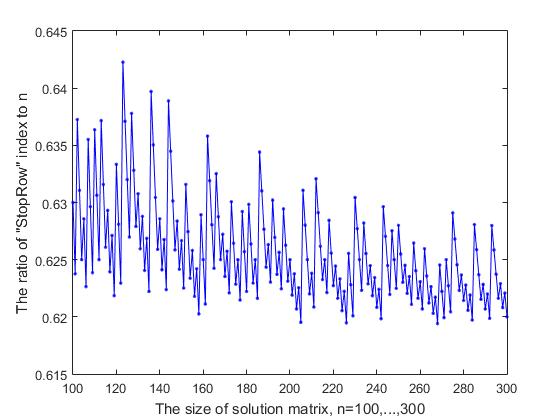
Fig. 9-2 Dependencia de la relación del índice StopRow a n en el tamaño de la matriz de decisión (parte 2)
El índice de la línea "StopRow", con el cual las dificultades comienzan a avanzar, depende del tamaño n de la matriz de decisión. Si consideramos la proporción de este índice, que denotamos por StopInd al tamaño de la matriz de solución n, entonces, como se puede ver en la Figura 9-1, donde se presentan los resultados de cálculo para los valores iniciales n = (7, ..., 99), esta proporción fluctúa en mayor o menor medida lado y tiende a disminuir. Con un aumento en n = (100, ..., 300), esta relación fluctúa entre 0.619 - 0.642 (Fig. 9-2), y con un aumento adicional en n, obtenemos los siguientes resultados (los valores de n se dan en secuencia, y el valor entre paréntesis es Relación StopInd y StopInd / n: 1000 (619, 0.6190), 2000 (1239, 0.6195), 3000 (1856, 0.6187), 4000 (2473, 0.6182), 5000 (3091, 0.6182). Sorprendentemente, se puede argumentar que detener -line divide la matriz de decisión de acuerdo con la regla de la proporción áurea : a saber, la relación StopInd / n difiere de (n-StopInd) / StopInd por una pequeña cantidad que tiende a cero al aumentar n. Por ejemplo, para n = 5000 la diferencia entre las relaciones 3091/5000 y 1909/3091 es 0.006, que es menos del 0.1% del promedio de estas dos relaciones.
El gráfico que se muestra en las dos figuras. 9- (1,2) tiene una variabilidad no aleatoria, que se asemeja a una grabación en un "pentagrama musical". Los saltos repetidos hacia arriba y la caída gradual son visibles con cierta periodicidad irregular. Obviamente, hay algún motivo para este tipo de comportamiento de curva, y quizás esto sea de interés para la investigación. Por esta razón, con el fin de una visualización más detallada, el gráfico se presentó en dos figuras.
Solo consideré una parte de las preguntas que pueden formularse sobre la base de los resultados de la solución del problema "sobre la distribución de n-reinas". Espero que los resultados obtenidos hagan que los mecanismos de formación de procesos no deterministas y los cambios en el espacio de estado sean más transparentes para la comprensión. Quizás esto sirva como punto de apoyo para la formulación de nuevas tareas y avanzar.
Conclusión
- Si, mirando la publicación, hemos llegado a una conclusión, entonces naturalmente surgirá la pregunta: "¿qué significa la Solución del problema de One Billion Queens en el título del artículo?" Al preparar la publicación para Habr, pensé que una persona que tiene, por ejemplo, una mina donde se extraen diamantes, debería dar al menos un diamante a sus amigos y familiares, de lo contrario sería injusto. Por lo tanto, me gustaría presentar un regalo a todos los miembros de la comunidad habr: participantes, organizadores, visitantes. Como su nombre lo indica, esta es la solución al problema de distribuir mil millones de reinas en un tablero de ajedrez de mil millones de mil millones.
Por supuesto, este no es un diamante facetado, pero para los verdaderos conocedores del arte intelectual, puede ser más valioso que "algún tipo de diamante allí". Además, los diamantes son muy diferentes en todo el mundo, y esta solución solo se encuentra en una copia hasta ahora. Y nuestro Byte-God (*) ve que estoy haciendo esto sinceramente.
La solución resultante es una matriz unidimensional de mil millones de números, que se presenta en formato MatLab .mat y está disponible en: One Billion Queens Problem Solution en Google Drive
-El primer elemento de esta matriz caracteriza la posición de la reina en la primera línea, el segundo elemento: la posición en la segunda línea, etc. Esta es solo una solución de nBillion de soluciones posibles. Y el valor de nBillion es un número tan grande que puede considerarse un pariente cercano del infinito.
- Me parece que esta solución puede atribuirse a la categoría de valores intelectuales virtuales. Podemos decir que "esto es algo en lo que hay algo". Realmente no pueden ser "tocados", por lo que se percibe en la conciencia solo al nivel de las sensaciones. Allí, de hecho, hay un orden sorprendente y una armonía explícita e implícita. Este es un regalo puramente simbólico (literal y figurado) dirigido a todos los miembros de la comunidad. Pienso: " No eres como todos los demás ".
(Espero que alguien "se lleve el regalo a casa". El archivo es lo suficientemente grande: 3,7 Gb. Se trata de datos limpios y verificados. Que Google Drive mostrará advertencias; trátelo con comprensión)
- Antes de tomar esta decisión, pensé en la naturaleza individual y colectiva de tal regalo. ¿Es posible que se presente uno con el original y el resto con copias? Pero la solución fue simple. Los conceptos habituales "cotidianos" de "original" y "copia", en este caso, pierden su significado. No copiamos, pero creamos otro original. Y los "originales" son iguales para todos e igualmente equivalentes.
- Creo que, en compañía de familiares, es muy probable que usted sea el único que recibió un "producto intelectual" como regalo. Será divertido si le cuenta a su suegra acerca de tal regalo: "Imagine una madre con un tablero de ajedrez que mide 50,000 km por 50,000 km, en el cual mil millones de reinas se distribuyen de tal manera que una no ve a la otra a corta distancia ...". Quién sabe, tal vez después de esto, el yerno será más apreciado, ya que se le da un regalo tan extraño.
Deseo a todos los miembros de la comunidad habr salud, éxito y bienestar. Que el año nuevo nos traiga buena suerte.
(*) - Ya que se refería al nombre del objeto, también se debe dar su descripción.
Byte Dios significa una entidad multidimensional, que consta de ceros y unos, razonable en todos los sentidos e infinita en todas las direcciones. Cualquier secuencia de ceros y unos en este espacio representa cierto conocimiento.
Referencias
[4] Max Bezzel, Propuesta de problema de 8 reinas ", Berliner Schachzeitung, Volumen
3 (1848), página 363. (Presentado bajo el nombre del autor \ Schachfreund ".)
[5] Franz Nauck, Briefwechseln mit allen fur alle ", Illustrirte Zeitung, Volumen
377 Número 15 (1850), página 182.
[6] Bell Jordan; Stevens Brett (2009). "Una encuesta de resultados conocidos y áreas de investigación para n-reinas". Matemática discreta. 309 (1): 1–31
[7] Gent, Ian P.; Jefferson, Christopher; Nightingale, Peter (agosto de 2017). "Complejidad de la finalización de n-Queens". Revista de Investigación de Inteligencia Artificial. AAAI Press. 59: 815–848
[8] W. Kosters y todos, n-Queens - 342 referencias, (20 de noviembre de 2018)
[9] NJA Sloane, la Enciclopedia en línea de secuencias enteras, publicada electrónicamente. 2016