Modelos matemáticos del caos

Introduccion

Habr ya discutió la teoría del caos en los artículos [1, 2, 3]. Los siguientes aspectos de la teoría del caos se consideran en estos artículos: diagrama generalizado del generador Chua; modelando la dinámica del sistema Lorentz; atractores programados por circuitos integrados lógicos Lorentz, Ressler, Rikitake y Nose-Hoover.

Sin embargo, las técnicas de la teoría del caos también se utilizan para modelar sistemas biológicos, que, sin duda, son uno de los sistemas más caóticos de todos los que se pueden imaginar. Se utilizaron sistemas de ecualización dinámica para modelar todo, desde el crecimiento de la población y la epidemia hasta los latidos cardíacos arrítmicos [4].

De hecho, casi cualquier sistema caótico puede ser modelado: el mercado de valores genera curvas que pueden analizarse fácilmente utilizando atractores extraños, el proceso de soltar gotas de un grifo que gotea es aleatorio cuando se analiza con el oído desnudo, pero si se presenta como un atractor extraño, se abre Un orden sobrenatural que no podía esperarse de los medios tradicionales.

El propósito de este artículo es examinar la teoría del caos usando el ejemplo de aumentar el número de poblaciones biológicas y duplicar el ciclo en sistemas mecánicos con visualización gráfica de modelos matemáticos basados ​​en programas intuitivos simples escritos en Python.

El artículo fue escrito con el propósito de enseñar, pero permitirá que incluso un lector sin experiencia en programación use los programas anteriores para resolver de forma independiente la mayoría de los nuevos problemas educativos sobre el tema del modelado del fenómeno del caos.

Duplicar el período de ciclos y caos en el ejemplo del crecimiento del número de poblaciones biológicas.

Comencemos observando la ecuación diferencial logística que modela un aumento limitado en lugar de exponencial en el número de poblaciones biológicas:

$$$\ frac {dN} {dt} = aN-bN ^ {2}, (a, b> 0). (1)$

Es esta ecuación la que puede predecir patrones de comportamiento exóticos e inesperados de algunas poblaciones. De hecho, de acuerdo con (1), para $$$t \ rightarrow + \ infty$El tamaño de la población se aproxima al límite igual a a / b .

Para la solución numérica de la solución diferencial logística, puede usar el algoritmo más simple, con el valor numérico del paso de tiempo, tomando $$$t_ {n + 1} = t_ {n} + h$, entonces la solución (1) se puede obtener aplicando repetidamente la siguiente relación:

$$$N_ {n + 1} = N_ {n} + (aN_n-bN {_ {n}} ^ {2}) h.$(2)

Representamos la ecuación (2) en forma de una ecuación logística en diferencias finitas:

$$$N_ {n + 1} = rN_ {n} -sN {_ {n}} ^ {2}$. (3)

donde: r = 1 + ah y s = bh .
Sustitución en (3) $$$N_ {n} = \ frac {r} {s} x_ {n}$obtenemos la fórmula iterativa:

$$$x_ {n + 1} = rx_ {n} (1-x_ {n})$, (4)

Calculando los valores dados por la relación (3), podemos generar una secuencia $$$x_ {1}, x_ {2}, x_ {3}, .....$
Los valores máximos de la cantidad de poblaciones que el medio ambiente soportará en determinados momentos. $$$t_ {1}, t_ {2}, t_ {3}.$.

Suponemos que hay un valor límite de fracciones que expresan una parte del tamaño de la población:

$$$x _ {\ infty} = \ lim_ {n \ to \ infty} x_ {n}$, (5).

Investigaremos cómo depende $$$x _ {\ infty}$del parámetro de crecimiento r en la ecuación (4). Para hacer esto, en Python, escribimos un programa que, comenzando con $$$x_ {1} = $ 0.$calcula los resultados en varios cientos de iteraciones ( n = 200 ) para r = 1.5; 2.0; 2.5 :


El resultado del programa (para reducir la salida de los resultados, se dan los primeros tres y últimos cuatro valores):

  nr=1,5 r=2,0 r=2,5 0 0.5000 0.5000 0.5000 1 0.3750 0.5000 0.6250 2 0.3516 0.5000 0.5859 . . . 197 0.3333 0.5000 0.6000 198 0.3333 0.5000 0.6000 199 0.3333 0.5000 0.6000 200 0.3333 0.5000 0.6000 

Un análisis del modelo discreto muestra que para r = 1.5; 2.0; 2.5 con un aumento en el número de iteraciones, el valor $$$x_ {n}$se estabiliza y se vuelve casi igual al límite $$$x _ {\ infty}$, que está determinado por la relación (5). Además, para los valores dados de r, la cantidad $$$x _ {\ infty}$correspondientemente igual $$$x _ {\ infty} = 0.3333; 0.5000; $ 0.600$.
Aumentamos r = 3.1; 3.25; 3.5 y el número de iteraciones n = 1008, para esto hacemos los siguientes cambios en el programa:


El resultado del programa (para reducir la salida de los resultados, se dan los primeros cuatro y últimos ocho valores):

  nr=3,1 r=3,25 r=3,5 0 0.5000 0.5000 0.5000 1 0.7750 0.8125 0.8750 2 0.5406 0.4951 0.3828 3 0.7699 0.8124 0.8269 . . . 1000 0.5580 0.4953 0.5009 1001 0.7646 0.8124 0.8750 1002 0.5580 0.4953 0.3828 1003 0.7646 0.8124 0.8269 1004 0.5580 0.4953 0.5009 1005 0.7646 0.8124 0.8750 1006 0.5580 0.4953 0.3828 1007 0.7646 0.8124 0.8269 

Como se desprende de los datos anteriores, en lugar de estabilizarse cerca de una sola población limitante, la parte fraccional de la población fluctúa entre dos fracciones a medida que cambia el tiempo. En comparación con r = 3.1 , el período del ciclo para r = 3.25 se duplica y para r = 3.5 cuatro veces.


El resultado del programa:



Debido a duplicar el período de iteración, $$$x_ {n + 1} = rx_ {n} (1-x_ {n})$se hizo ampliamente conocido. Cuando el valor de la tasa de crecimiento excede r = 3.56 , la duplicación del período se acelera y el caos extremo ya surge en el punto r = 3.57 . Para mostrar el inicio del caos, utilizamos el siguiente programa:


El resultado del programa:

  nr=3,57 1000 0.4751 1001 0.8903 1002 0.3487 1003 0.8108 1004 0.5477 1005 0.8844 1006 0.3650 1007 0.8275 1008 0.5096 1009 0.8922 1010 0.3434 1011 0.8050 1012 0.5604 1013 0.8795 1014 0.3784 1015 0.8397 

Escribiremos un programa para visualizar la dependencia del comportamiento de iteración en el parámetro de crecimiento r . Para cada valor de r en el intervalo $$$a \ leqslant r \ leqslant b$Se realizan 1000 iteraciones para lograr la estabilidad. Luego, cada 250 valores obtenidos como resultado de iteraciones se trazan a lo largo del eje vertical, formando puntos ( r, x ):


El resultado en forma de diagrama:



El gráfico resultante se denomina "diagrama de ramificación" , que le permite determinar si un valor r dado corresponde a un ciclo o caos. El único valor del tamaño de la población se determina al valor $$$r \ aproximadamente 3$luego un ciclo con un período de 2 a $$$r \ aproximadamente 3.4$, luego un ciclo con un período de 4, luego un ciclo con un período de 8 en adelante con un acercamiento rápido al caos.

Cabe señalar que las áreas verticales de espacio sin llenar en el gráfico son las regiones r = 3.6 y r = 3.7 , entre r = 3.7 y r = 3.8 , entre r = 3.8 y r = 3.9 donde el orden cíclico regresa del caos anterior.
Considerar la aparición de un ciclo con un período múltiplo de 3 en la región. $$$3.8 \ leqslant r \ leqslant $ 3.$hacer cambios al programa anterior:


El resultado del programa:



El ciclo del período 3 aparece cerca del punto r = 3.83 , y luego se divide secuencialmente en los ciclos 6,12,24. La existencia de un ciclo con período 3 implica la presencia de ciclos de cualquier otro período finito, así como ciclos caóticos sin ningún período en absoluto.

El diagrama de ramificación le permite seguir el desarrollo del sistema con un cambio suave en el parámetro. Con un valor fijo del parámetro, el diagrama de araña (diagrama de Lamera) permite trazar las órbitas de los puntos.

La construcción de un diagrama de araña le permite identificar varios efectos que son invisibles en el diagrama de rama. Escribamos un programa:


Diagrama de Lamera:

Período de duplicación en sistemas mecánicos

Considere una ecuación diferencial que modela las vibraciones amortiguadas libres de un punto material de una masa dada en un resorte no lineal, en el que la amortiguación está determinada por la velocidad.

$$$mx ^ {''} + cx ^ {'} + kx + \ beta x ^ {3} = 0$(6)

En la ecuación (6), el término kx representa la fuerza de un resorte lineal aplicado a un punto material de una masa dada, y el término $$$\ beta x ^ {3}$representa la no linealidad real de la primavera.

Si una fuerza actúa sobre el sistema de oscilaciones libres (6), la ecuación diferencial de Duffing para oscilaciones forzadas describe el desplazamiento del punto material de la masa a la que se aplica esta fuerza:

$$$mx ^ {''} + cx ^ {'} + kx + \ beta x ^ {3} = F_ {0} cos \ omega t$(7)

La ecuación (7) para la mayoría de los parámetros incluidos se resuelve numéricamente. El sistema mecánico para el modelo matemático de acuerdo con la ecuación (7) se muestra en la figura:



Una característica del sistema dado es que, en lugar de un resorte, se usa un hilo de metal flexible, que oscila en un plano vertical, para el cual la constante de gancho k es negativa. En este esquema, los puntos de equilibrio estable (a) y (c), y el punto de equilibrio inestable (b).

Cuando un punto material se desplaza de la posición (b), la fuerza que actúa sobre él es repulsiva. Si la fuerza periódica, por ejemplo, creada por el campo magnético oscilante está parcialmente amortiguada por la resistencia del aire. Entonces, la ecuación (7) es un modelo matemático aceptable para el desplazamiento horizontal x (t) de un punto material con los siguientes rangos de parámetros $$$k <0, c> 0, \ beta> 0$.

Para estudiar el comportamiento de dicho sistema no lineal, tomamos $$$k = -1, m = c = \ beta = \ omega = 1$entonces la ecuación diferencial (7) toma la forma:

$$$x ^ {''} + x ^ {'} - x + x ^ {3} = F_ {0} cos (t)$, (8)

Escribimos un programa para la integración numérica de la ecuación (8) bajo las condiciones iniciales $$$x (0) = 1, x ^ {'} (0) = 0$en el campo $$$100 \ leqslant t \ leqslant 200$y para cada uno de los siguientes valores de amplitud $$$F_ {0} = 0.6; 0.7; 0.75; 0.8$, y en cada caso, grafica las soluciones para los planos $$$x (t), x ^ {'} (t)$y $$$t, x (t)$:


Gráficos como resultado del programa





Esta transición del período doble al caos muestra el comportamiento general de un sistema mecánico no lineal en respuesta a un cambio en el parámetro físico correspondiente, por ejemplo: $$$k, m, c, \ beta, \ omega, F_ {0}$. Tales fenómenos no ocurren en sistemas mecánicos lineales.

Atractor Lorenz

La sustitución en la ecuación de Duffing por oscilaciones forzadas (7) conduce a un sistema bidimensional no lineal de ecuaciones diferenciales, que se mostró en la lista anterior. E.N. consideró un sistema tridimensional no lineal de ecuaciones diferenciales aplicado a problemas meteorológicos. Lorenz:

$$$\ frac {dx} {dt} = - sx + sy,$
$$$\ frac {dy} {dt} = - xz + rx-y,$(9)
$$$\ frac {dz} {dt} = xy-dz$

La solución al sistema (9) se ve mejor en proyección en uno de los tres planos. Escribimos un programa de integración numérica para los valores de los parámetros b = \ frac {8} {3}, s = 10, r = 28 y las condiciones iniciales x (0) = - 8, y (0) = 8, z (0) = 27 :


El resultado del programa:



Teniendo en cuenta la imagen en el gráfico a lo largo del tiempo, se puede suponer que el punto P (x (t), y (t), z (t)) genera un número aleatorio de oscilaciones, derecha o izquierda. Para una aplicación meteorológica del sistema Lorenz, después de un número aleatorio de días despejados, sigue un número aleatorio de días lluviosos.

Considere un programa para mapear el atractor de Lorentz en el plano xyz para condiciones iniciales ligeramente diferentes:


Los resultados del programa se muestran en los siguientes gráficos:





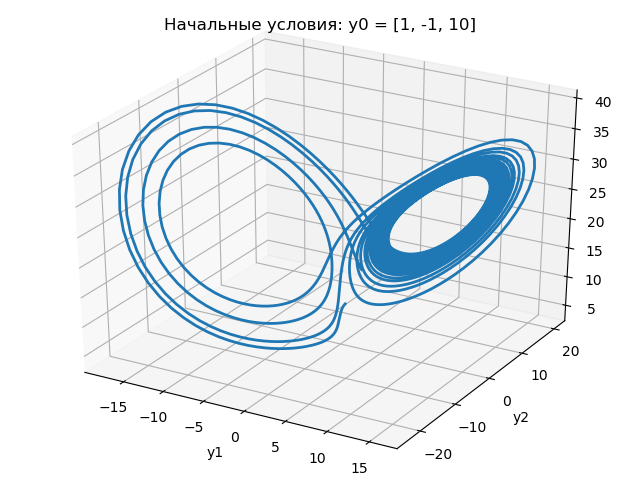
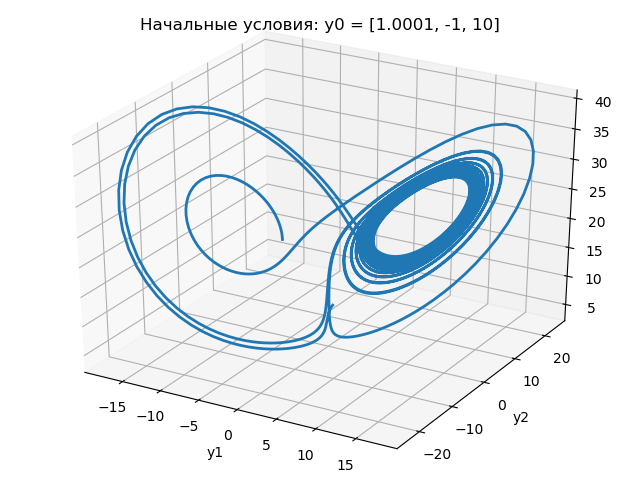
De los gráficos anteriores se deduce que un cambio en la condición inicial de 1.0 a 1.0001 cambia drásticamente la naturaleza del cambio en el atractor de Lorentz.

Sistema de Rossler

Este es un sistema tridimensional no lineal muy estudiado:
$$$\ frac {dx} {dt} = - y-z,$
$$$\ frac {dy} {dt} = x- \ alpha y,$(10)
$$$\ frac {dz} {dt} = b + x (x-c).$

Escribiremos un programa para la integración numérica del sistema (10) para los siguientes parámetros a = 0.39, b = 2, c = 4 bajo las condiciones iniciales x (0) = 0, y (0) = 0, z (0) = 0 :


El resultado del programa:



En el avión, la cinta de Rossler parece un lazo, pero en el espacio parece estar torcida como una cinta de Moebius.

Conclusiones

Para demostrar los fenómenos del caos, se presentan programas simples e intuitivos en un lenguaje de programación Python de alto nivel, que son fáciles de actualizar a nuevos proyectos sobre este tema. El artículo tiene un enfoque educativo y metodológico y puede usarse en el proceso de aprendizaje.

Referencias

1. Un poco sobre el caos y cómo crearlo
2. Una mirada crítica al atractor de Lorenz
3. FPGA Chaos Generators
4. Ecuaciones diferenciales y problemas de valor límite: modelado y cálculo usando Mathematica, Maple y MATLAB. 3ª edición.: Per. del ingles - M .: LLC "I.D. Williams, 2008. - 1104 p .: Ill. - Paral. tit. Ingles