Biquaternions

Si abrió este artículo, probablemente ya haya escuchado sobre los cuaterniones, y tal vez incluso los use en sus diseños. Pero es hora de ascender a un nivel superior, a los biquaternions.

Este artículo ofrece conceptos básicos sobre biquaternions y operaciones con ellos. Para una mejor comprensión del trabajo con biquaternions, se muestra un claro ejemplo en Javascript usando Canvas.

Biquaternion

Biquaternion es un número hipercomplejo que tiene una dimensión de 8. En los artículos y la literatura en inglés se les llama "dual quaternion", y en la literatura en ruso también se encuentran los nombres "dual quaternion" o "quaternion complejo".

La principal diferencia con los cuaterniones es que el cuaternión describe la orientación del objeto en el espacio, y el biquaternion también describe la posición del objeto en el espacio.

Biquaternion se puede representar como dos cuaterniones:

$$

$$\ widetilde {\ textbf {q}} = \ begin {bmatrix} \ textbf {q} _1 \\ \ textbf {q} _2 \ end {bmatrix},$$

$$$\ textbf {q} _1$ - la parte real, determina la orientación del objeto en el espacio;
$$$\ textbf {q} _2$ - la parte dual, determina la posición del objeto en el espacio.

El biquaternion también se llama cuaternión complejo, en este caso se representa como un cuaternión, cada componente del cual es un número dual (que no debe confundirse con el complejo). Número dual $$$A = a_1 + \ epsilon a_2$ donde $$$a_1$ y $$$a_2$ Son números reales y $$$\ epsilon$ - Símbolo de Clifford (complejidad), que posee la propiedad $$$\ epsilon ^ 2 = 0$ . No profundizaremos en las matemáticas, ya que estamos más interesados ​​en la parte aplicada, por lo tanto, consideraremos el biquaternion como dos cuaterniones.

Interpretación geométrica de biquaternion

Por analogía con el cuaternión, con el que puede establecer la orientación del objeto, el biquaternion también puede establecer la posición. Es decir El biquaternion establece dos valores a la vez: la posición y orientación del objeto en el espacio. Si los consideramos en dinámica, entonces el biquaternion define dos cantidades: la velocidad lineal de movimiento y la velocidad angular de rotación del objeto. La siguiente figura muestra el significado geométrico de biquaternion.



Los desarrolladores de juegos saben que para determinar la posición y orientación de un objeto en el espacio del juego, se utilizan matrices de rotación y matrices de desplazamiento y, según el orden en que las aplique, el resultado de la posición final del objeto es diferente. Para aquellos que están acostumbrados a dividir el movimiento en operaciones separadas, acepten la regla para trabajar con biquaternions: primero movemos el objeto, luego lo rotamos. De hecho, está describiendo estos dos movimientos con un solo número, aunque sea un hipercomplejo complejo.

Características escalares

Considere las principales características escalares. Aquí es necesario prestar atención al hecho de que no devuelven números reales ordinarios, sino dobles.

1. La norma del biquaternion

$$

$$\ | \ widetilde {\ textbf {q}} \ | = \ | \ textbf {q} _1 \ | + \ epsilon (q_ {1_0} q_ {2_0} + \ textbf {q} _1 ^ T \ textbf {q} _2)$$

2. Módulo biquaternion

$$

$$| \ widetilde {\ textbf {q}} | = | \ textbf {q} _1 | + \ epsilon \ frac {q_ {1_0} q_ {2_0} + \ textbf {q} _1 ^ T \ textbf {q} _2} {| \ textbf {q} _1 |}$$

Operaciones básicas

Considere las operaciones básicas de trabajar con biquaternions. Como puede ver, son muy similares a operaciones similares con cuaterniones.

1. Emparejamiento de biquaternion

$$

$$\ widetilde {\ textbf {q}} ^ * = \ begin {bmatrix} \ textbf {q} _1 ^ * \\ \ textbf {q} _2 ^ * \ end {bmatrix}$$

2. Suma y resta biquaternion

$$

$$\ widetilde {\ textbf {q}} \ pm \ widetilde {\ textbf {p}} = \ begin {bmatrix} \ textbf {q} _1 \ pm \ textbf {p} _1 \\ \ textbf {q} _2 \ pm \ textbf {p} _2 \ end {bmatrix}$$

La suma y resta de biquaternions es conmutativa (los términos pueden intercambiarse).

3. Multiplicación del número real por biquaternion

$$

$$a \ widetilde {\ textbf {q}} = \ widetilde {\ textbf {q}} a = \ begin {bmatrix} a \ textbf {q} _1 \\ a \ textbf {q} _2 \ end {bmatrix}$$

4. Multiplicación biquaternion

$$

$$\ widetilde {\ textbf {q}} \ otimes \ widetilde {\ textbf {p}} = \ begin {bmatrix} \ textbf {q} _1 \ otimes \ textbf {p} _1 \\ \ textbf {q} _1 \ otimes \ textbf {p} _2 + \ textbf {q} _2 \ otimes \ textbf {p} _1 \ end {bmatrix}$$

La multiplicación de biquaternion no es conmutativa (con un cambio en el orden de los factores, el resultado de la multiplicación de biquaternion es diferente).

Esta operación es una de las principales cuando se trabaja con biquaternions y tiene un significado físico, es decir, el resultado de la multiplicación de biquaternion es la operación de sumar las rotaciones y los movimientos lineales de dos biquaternions.

5. Biquaternion inverso

$$

$$\ widetilde {\ textbf {q}} ^ {- 1} = \ frac {\ widetilde {\ textbf {q}} ^ *} {\ | \ widetilde {\ textbf {q}} \ |}$$

Determinación de biquaternion a través de ángulos de orientación y vector de posición

Primero, definimos los sistemas de coordenadas en los que consideraremos la orientación y posición del objeto en el espacio. Esto debe hacerse para especificar la parte real del biquaternion (cuaternión de orientación), cuya secuencia de rotación afecta al cuaternión resultante desde los ángulos de orientación. Aquí nos guiaremos por los ángulos del avión - yaw $$$\ psi$ tono $$$\ vartheta$ y rodar $$$\ gamma$ .

Definir el sistema de coordenadas base. Imagina que estás parado en la superficie de la Tierra y mirando en dirección al Norte.

Punto O _o : el origen del sistema de coordenadas, ubicado en el punto de origen del objeto.
El eje O _o Y _g - se dirige verticalmente hacia arriba y es opuesto a la dirección del vector de gravedad.
El eje O _o X _g - se dirige hacia el norte, a lo largo de la tangente del meridiano local.
Eje O _o Z _g : complementa el sistema hacia la derecha y se dirige hacia la derecha, hacia el Este.

El segundo sistema de coordenadas está conectado. Imagine, por ejemplo, un avión u otro objeto.
Punto O : el origen del sistema de coordenadas, por regla general, se encuentra en el punto del centro de masa del objeto.
Eje OY : dirigido verticalmente hacia arriba y perpendicular al plano horizontal del objeto.
Axis OX : dirigido hacia el punto frontal del objeto.
Eje OZ : complementa el sistema a la derecha.

La posición del objeto en el espacio está determinada por el vector de radio del origen (punto O ) del sistema de coordenadas asociado en relación con el sistema de coordenadas base fijo. La orientación del sistema de coordenadas asociado en relación con la base se determina mediante tres vueltas sucesivas:

ángulo de guiñada $$$\ psi$ - rotación alrededor del eje OY ,
ángulo de inclinación $$$\ vartheta$ - rotación alrededor del eje OZ ,
ángulo de balanceo $$$\ gamma$ - rotación alrededor del eje OX .

Para la determinación inicial de biquaternion, debe especificar las partes real y dual del biquaternion. La orientación y posición del objeto se establece en relación con un determinado sistema de coordenadas de base utilizando ángulos de orientación. $$$\ psi, \ vartheta, \ gamma$ y vector de posición del centro de masa $$$r = (r_x, r_y, r_z) ^ T$ .

La parte real $$$\ textbf {q} _1$ se puede configurar con la fórmula:

$$

$$\ textbf {q} _1 = \ begin {bmatrix} \ cos \ frac {\ psi} {2} \ cos \ frac {\ vartheta} {2} \ cos \ frac {\ gamma} {2} & - & \ sin \ frac {\ psi} {2} \ sin \ frac {\ vartheta} {2} \ sin \ frac {\ gamma} {2} \\ \ cos \ frac {\ psi} {2} \ cos \ frac { \ vartheta} {2} \ sin \ frac {\ gamma} {2} & + & \ sin \ frac {\ psi} {2} \ sin \ frac {\ vartheta} {2} \ cos \ frac {\ gamma} {2} \\ \ cos \ frac {\ psi} {2} \ sin \ frac {\ vartheta} {2} \ sin \ frac {\ gamma} {2} & + y \ sin \ frac {\ psi} { 2} \ cos \ frac {\ vartheta} {2} \ cos \ frac {\ gamma} {2} \\ \ cos \ frac {\ psi} {2} \ sin \ frac {\ vartheta} {2} \ cos \ frac {\ gamma} {2} & - & \ sin \ frac {\ psi} {2} \ cos \ frac {\ vartheta} {2} \ sin \ frac {\ gamma} {2} \ end {bmatrix} $$$

Tenga en cuenta que si tiene una secuencia de rotación diferente, las expresiones también serán diferentes.

Parte dual $$$\ textbf {q} _2$ definido por la expresión:

$$

$$\ textbf {q} _2 = \ frac12 \ textbf {r} \ otimes \ textbf {q} _1$$

Cálculo de ángulos de orientación y vector de posición a partir de biquaternion. Transformación inversa

Los ángulos de orientación se pueden calcular a partir de la parte real del biquaternion $$$\ textbf {q} _1$ :

$$

$$\ psi = \ arctan {\ frac {2 (q_0 q_2 - q_1 q_3)} {q_0 ^ 2 + q_1 ^ 2 - q_2 ^ 2 - q_3 ^ 2}}$$

$$

$$\ vartheta = \ arcsin {(2 (q_1 q_2 + q_0 q_3))}$$

$$

$$\ gamma = \ arctan {\ frac {2 (q_0 q_1 - q_2 q_3)} {q_0 ^ 2 - q_1 ^ 2 + q_2 ^ 2 - q_3 ^ 2}}$$

La posición del objeto está determinada por la expresión:

$$

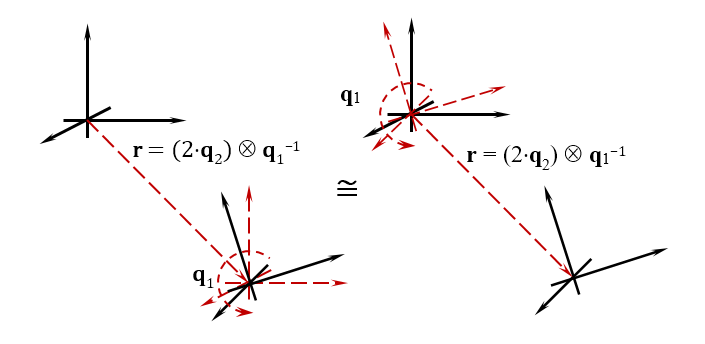
$$\ textbf {r} = 2 \ textbf {q} _2 \ otimes \ textbf {q} _1 ^ {- 1}$$

el resultado es un vector en forma de cuaternión $$$\ textbf {r} = (0, r_x, r_y, r_z) ^ T$

Rotar y mover el vector biquaternion

Una de las grandes propiedades de los biquaternions es la rotación y el movimiento de un vector de un sistema de coordenadas a otro. Sea O _o X _g Y _g Z _g un sistema de coordenadas base fijo, y OXYZ sea ​​el sistema de coordenadas conectado del objeto. Entonces el biquaternion puede especificar la orientación y posición del objeto en relación con el sistema de coordenadas base. $$$\ widetilde {\ textbf {q}}$ . Si se especifica un vector $$$\ textbf {r}$ en un sistema de coordenadas conectado, entonces puedes obtener un vector $$$\ textbf {r} _0$ en el sistema de coordenadas base usando la fórmula:

$$

$$\ textbf {r} _0 = \ widetilde {\ textbf {q}} \ otimes \ textbf {r} \ otimes \ widetilde {\ textbf {q}} ^ {- 1}$$

y de regreso:

$$

$$\ textbf {r} = \ widetilde {\ textbf {q}} ^ {- 1} \ otimes \ textbf {r} _0 \ otimes \ widetilde {\ textbf {q}}$$

donde $$$\ textbf {r}$ Es un vector en forma de biquaternion, $$$\ textbf {r} = (1, 0, 0, 0, 0, 0, r_x, r_y, r_z)$

Biquaternion JavaScript Library

Todas las operaciones anteriores con biquaternions se implementan en la biblioteca javascript, dependiendo de sus tareas, se puede implementar en otros lenguajes de programación. Las principales funciones de trabajar con biquaternions:

Función	Descripción
DualQuaternion.dq	Biquaternion cuerpo como una matriz de 8 números
DualQuaternion(dq0, dq1, dq2, dq3, dq4, dq5, dq6, dq7)	Un constructor que define un biquaternion especificando los ocho números.
DualQuaternion.fromEulerVector(psi, theta, gamma, v)	Obtenga biquaternion configurando la orientación del objeto con ángulos de Euler y el vector de posición del objeto
DualQuaternion.getEulerVector()	Obtenga los ángulos de Euler y el vector de posición de biquaternion
DualQuaternion.getVector()	Obtener el vector de posición de biquaternion
DualQuaternion.getReal()	Obtenga la parte real del biquaternion (determina la orientación del objeto en el espacio)
DualQuaternion.getDual()	Obtenga la parte dual del biquaternion (determina la posición del objeto en el espacio)
DualQuaternion.norm()	Obtenga la norma del biquaternion como un número dual
DualQuaternion.mod()	Obtenga el módulo biquaternion como un número dual
DualQuaternion.conjugate()	Consigue el biquaternion conjugado
DualQuaternion.inverse()	Consigue el biquaternion inverso
DualQuaternion.mul(DQ2)	Biquaternion multiplication
DualQuaternion.toString()	Convierta biquaternion en una cadena, por ejemplo, para la salida a la consola de depuración

Un ejemplo de trabajo con biquaternions

Para una mejor comprensión de los conceptos básicos del uso de biquaternions como ejemplo, considere un juego pequeño. Se establece el área rectangular: el mapa. Un barco flotando en un mapa con una pistola giratoria montada en el mapa. Aquí es necesario tener en cuenta que para el barco el sistema de coordenadas básico es el sistema de coordenadas del mapa, y para el arma el sistema de coordenadas básico es el barco. Todos los objetos se dibujan en el sistema de coordenadas del mapa y aquí será interesante ver cómo puede pasar del sistema de coordenadas de la pistola al sistema de coordenadas del mapa utilizando la propiedad de multiplicación del biquaternion. El movimiento del barco está controlado por las teclas W, A, S, D. La dirección de la pistola se establece con el cursor del mouse.



El barco y el arma se describen en dos clases: Ship y Gun . En el constructor de la clase de barco, se establece su forma en forma de puntos de biquaternion, la orientación inicial y la posición en el mapa en forma de this.dq_pos biquaternion.

Los incrementos de biquaternion también se dan para el control del barco. Al moverse hacia adelante y hacia atrás (teclas W, S), solo cambiará la parte dual del biquaternion, y al controlar a izquierda y derecha (teclas A, D), la parte real y dual del biquaternion cambiará, lo que establece el ángulo de rotación.

 function Ship(ctx, v) { this.ctx = ctx; this.dq_pos = new DualQuaternion.fromEulerVector(0*Math.PI/180, 0, 0, v); //   this.dq_forward_left = new DualQuaternion.fromEulerVector(0, 0, 0, [ 15, 0, -10]); this.dq_forward_right = new DualQuaternion.fromEulerVector(0, 0, 0, [ 15, 0, 10]); this.dq_backward_left = new DualQuaternion.fromEulerVector(0, 0, 0, [-15, 0, -10]); this.dq_backward_right = new DualQuaternion.fromEulerVector(0, 0, 0, [-15, 0, 10]); this.dq_forward_forward = new DualQuaternion.fromEulerVector(0, 0, 0, [ 30, 0, 0]); //      this.dq_dx_left = new DualQuaternion.fromEulerVector( 1*Math.PI/180, 0, 0, [0, 0, 0]); this.dq_dx_right = new DualQuaternion.fromEulerVector(-1*Math.PI/180, 0, 0, [0, 0, 0]); this.dq_dx_forward = new DualQuaternion.fromEulerVector(0, 0, 0, [ 1, 0, 0]); this.dq_dx_backward = new DualQuaternion.fromEulerVector(0, 0, 0, [-1, 0, 0]); return this; }; 

En la clase misma, solo hay una función para representar el barco Ship.draw() . Tenga en cuenta la aplicación de la operación biquaternion de multiplicar cada punto del barco con el biquaternion de la posición actual y la orientación del barco.

 Ship.prototype = { 'ctx': 0, 'dq_pos': new DualQuaternion.fromEulerVector(0, 0, 0, 0, 0, 0), /** *   */ 'draw': function() { //         v_pos = this.dq_pos.getVector(); v_forward_left = this.dq_pos.mul(this.dq_forward_left).getVector(); v_forward_right = this.dq_pos.mul(this.dq_forward_right).getVector(); v_backward_left = this.dq_pos.mul(this.dq_backward_left).getVector(); v_backward_right = this.dq_pos.mul(this.dq_backward_right).getVector(); v_forward_forward = this.dq_pos.mul(this.dq_forward_forward).getVector(); //   ctx.beginPath(); ctx.moveTo(v_backward_left[0], v_backward_left[2]); ctx.lineTo(v_forward_left[0], v_forward_left[2]); ctx.lineTo(v_forward_left[0], v_forward_left[2]); ctx.lineTo(v_forward_forward[0], v_forward_forward[2]); ctx.lineTo(v_forward_right[0], v_forward_right[2]); ctx.lineTo(v_backward_right[0], v_backward_right[2]); ctx.lineTo(v_backward_left[0], v_backward_left[2]); ctx.stroke(); ctx.closePath(); } }; 

En el constructor de la clase de arma, se especifica su forma en forma de puntos de biquaternion. La pistola se mostrará como una línea. La orientación inicial y la posición en el barco se establecen mediante el this.dq_pos this.dq_pos. Además, también se establece el enlace al barco en el que está instalado. El arma en la nave solo puede girar, por lo que los incrementos de biquaternion al controlar el arma solo cambiarán la parte real del biquaternion, que establece el ángulo de rotación. En este ejemplo, el implemento es guiado por el cursor del mouse, por lo que la rotación de la pistola se producirá instantáneamente.

 function Gun(ctx, ship, v) { this.ctx = ctx; this.ship = ship; //     this.dq_pos = new DualQuaternion.fromEulerVector(0, 0, 0, v); //   this.dq_forward = new DualQuaternion.fromEulerVector(0, 0, 0, [20, 0, 0]); this.dq_backward = new DualQuaternion.fromEulerVector(0, 0, 0, [ 0, 0, 0]); //     this.dq_dx_left = new DualQuaternion.fromEulerVector( 1*Math.PI/180, 0, 0, [0, 0, 0]); this.dq_dx_right = new DualQuaternion.fromEulerVector(-1*Math.PI/180, 0, 0, [0, 0, 0]); return this; }; 

En la clase de arma, solo Ship.draw() implementa una función de su representación Ship.draw() . La pistola se muestra como una línea, que se establece por dos puntos this.dq_backward y this.dq_forward . Para determinar las coordenadas de los puntos de la pistola, se utiliza la operación de multiplicación biquaternion.

 Gun.prototype = { 'ctx': 0, 'ship': 0, 'dq_pos': new DualQuaternion.fromEulerVector(0, 0, 0, [0, 0, 0]), /** *   */ 'draw': function() { //     v_pos = this.ship.dq_pos.getVector(); v_forward = this.ship.dq_pos.mul(this.dq_backward).mul(this.dq_forward).getVector(); v_backward = this.ship.dq_pos.mul(this.dq_backward).getVector(); //   ctx.beginPath(); ctx.moveTo(v_backward[0], v_backward[2]); ctx.lineTo(v_forward[0], v_forward[2]); ctx.stroke(); ctx.closePath(); } }; 

El procesamiento del control de buques y armas se implementa a través de eventos. Cuatro variables leftPressed, upPressed, rightPressed, downPressed , que se procesan en el bucle principal del programa, son responsables de presionar y soltar las teclas de control del barco.

 leftPressed = false; rightPressed = false; upPressed = false; downPressed = false; dq_mouse_pos = new DualQuaternion.fromEulerVector(0, 0, 0, [0, 0, 0]); document.addEventListener("keydown", keyDownHandler, false); document.addEventListener("keyup", keyUpHandler, false); document.addEventListener("mousemove", mouseMoveHandler, false); //     function keyDownHandler(e) { if (e.keyCode == 37 || e.keyCode == 65 || e.keyCode == 97) { leftPressed = true; } //  A else if (e.keyCode == 38 || e.keyCode == 87 || e.keyCode == 119) { upPressed = true; } //  W else if (e.keyCode == 39 || e.keyCode == 68 || e.keyCode == 100) { rightPressed = true; } //  D else if (e.keyCode == 40 || e.keyCode == 83 || e.keyCode == 115) { downPressed = true; } //  S } //     function keyUpHandler(e) { if (e.keyCode == 37 || e.keyCode == 65 || e.keyCode == 97) { leftPressed = false; } //  A else if (e.keyCode == 38 || e.keyCode == 87 || e.keyCode == 119) { upPressed = false; } //  W else if (e.keyCode == 39 || e.keyCode == 68 || e.keyCode == 100) { rightPressed = false; } //  D else if (e.keyCode == 40 || e.keyCode == 83 || e.keyCode == 115) { downPressed = false; } //  S } 

Una de las funciones más interesantes, desde el punto de vista del uso de las operaciones de biquaternion, es controlar el arma del barco en la dirección del puntero del mouse. Primero, las coordenadas del puntero del mouse se determinan en el dq_mouse_pos dq_mouse_pos. Luego, el biquaternion de la posición del mouse con respecto a la nave se calcula utilizando la multiplicación biquaternion. El biquaternion del barco se toma del mouse biquaternion dq_mouse_pos_about_ship = ship_1.dq_pos.inverse().mul(dq_mouse_pos);
(Nota: las operaciones de multiplicación de biquaternion secuenciales se leen de derecha a izquierda). Finalmente, se determina el ángulo entre la herramienta y los vectores del mouse. El punto de inicio de la pistola gun_1.dq_backward asignado el valor recibido.

 function mouseMoveHandler(e) { var relativeX = e.clientX - canvas.offsetLeft; var relativeY = e.clientY - canvas.offsetTop; //           if (relativeX > 0 && relativeX < canvas.width && relativeY > 0 && relativeY < canvas.height) { //    dq_mouse_pos = new DualQuaternion.fromEulerVector(0, 0, 0, [relativeX, 0, relativeY]); //      //  .       //     // DQ_ship^(-1) * DQ_mouse dq_mouse_pos_about_ship = ship_1.dq_pos.inverse().mul(dq_mouse_pos); //       q_gun_mouse = new Quaternion.fromBetweenVectors(gun_1.dq_forward.getVector(), dq_mouse_pos_about_ship.getVector()); dq_gun_mouse = new DualQuaternion(q_gun_mouse.q[0], q_gun_mouse.q[1], q_gun_mouse.q[2], q_gun_mouse.q[3], 0, 0, 0, 0); gun_1.dq_backward = dq_gun_mouse; // console.log(dq_gun_mouse.getEulerVector()); // console.log(relativeX + ' ' + relativeY + ' ' + gun_1.dq_forward.toString()); } } 

En el cuerpo principal del programa, los objetos del barco y las armas ship_1 y gun_1 , se muestra la información de depuración y se lleva a cabo el procesamiento del control del barco.

 var canvas = document.getElementById("myCanvas"); var ctx = canvas.getContext("2d"); ship_1 = new Ship(ctx, [100, 0, 100]); gun_1 = new Gun(ctx, ship_1, [0, 0, 0]); function draw() { ctx.clearRect(0, 0, canvas.width, canvas.height); ship_1.draw(); gun_1.draw(); // Debug info ship_euler_vector = ship_1.dq_pos.getEulerVector(); ship_euler_vector[0] = ship_euler_vector[0]*180/Math.PI; ship_euler_vector[1] = ship_euler_vector[1]*180/Math.PI; ship_euler_vector[2] = ship_euler_vector[2]*180/Math.PI; ship_euler_vector = ship_euler_vector.map(function(each_element){ return each_element.toFixed(2); }); ship_dq = ship_1.dq_pos.dq.map(function(each_element){ return each_element.toFixed(2); }); gun_dq = ship_1.dq_pos.mul(gun_1.dq_backward).dq.map(function(each_element){ return each_element.toFixed(2); }); ctx.font = "8pt Courier"; ctx.fillText("Ship: " + ship_dq + " | psi, theta, gamma, vector:" + ship_euler_vector, 10, 20); ctx.fillText("Gun: " + gun_dq, 10, 40); //   if (leftPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_left); } if (rightPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_right); } if (upPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_forward); } if (downPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_backward); } requestAnimationFrame(draw); } draw(); 

El enlace al archivo contiene el código completo de las bibliotecas para trabajar con quaternions y biquaternions, el script del programa en sí y el archivo index.html, que se puede abrir localmente en el navegador para ejecutar el ejemplo anterior.

Un ejemplo de trabajo con biquaternions

Conclusión

Puede tener una pregunta: ¿por qué usar un aparato matemático tan complejo cuando puede sobrevivir con herramientas estándar para mover y rotar objetos? Una de las principales ventajas es que la forma de escritura biquaternion es más computacionalmente eficiente, ya que todas las operaciones con biquaternions después de que las expresiones se expanden son lineales. Este video, Geometric Skinning with Approximate Dual Quaternion Blending, muestra cuánto más eficientes son los cálculos de biquaternion que otros métodos.

Principalmente tomé información sobre el uso de biquaternions de fuentes inglesas.
De la literatura nacional, puedo aconsejar dos libros:

1. Chelnokov Yuri Nikolaevich. Modelos y métodos de mecánica de sólidos y sus aplicaciones. Geometría y cinemática del movimiento. - trabajo teórico monumental.
2. Gordeev Vadim Nikolaevich. Cuaterniones y biquaterniones con aplicaciones en geometría y mecánica. - Está escrito en un lenguaje más comprensible y muestra aplicaciones en las tareas de conformar estructuras espaciales curvas.