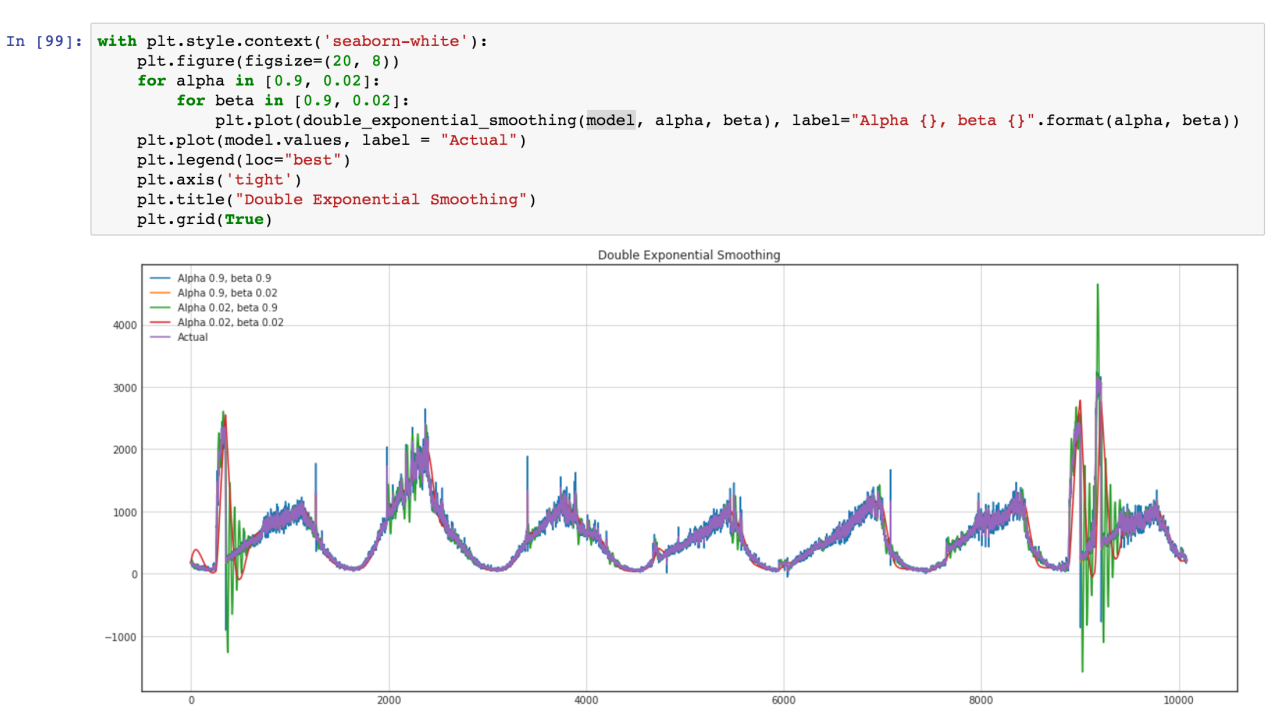
Este es un breve artículo sobre la comprensión de las series de tiempo y las principales características detrás de eso.
Declaración de problemas
Tenemos datos de series temporales con regularidad diaria y semanal. Queremos encontrar la forma de modelar estos datos de manera óptima.

Analizando series de tiempo
Una de las características importantes de las series temporales es la estacionariedad.
En matemática y estadística, un proceso estacionario (también conocido como un proceso estacionario estricto (ly) o un proceso estacionario fuerte (ly)) es un proceso estocástico cuya distribución de probabilidad conjunta no cambia cuando se desplaza en el tiempo.
En consecuencia, parámetros como la media y la varianza, si están presentes, tampoco cambian con el tiempo. Dado que la estacionariedad es una suposición subyacente en muchos procedimientos estadísticos utilizados en el análisis de series de tiempo, los datos no estacionarios a menudo se transforman en estacionarios.
La causa más común de violación de la estacionariedad son las tendencias en la media, que pueden deberse a la presencia de una raíz unitaria o de una tendencia determinista. En el primer caso de una raíz unitaria, los choques estocásticos tienen efectos permanentes y el proceso no es reversible. En el último caso de una tendencia determinista, el proceso se denomina proceso estacionario de tendencia, y los choques estocásticos solo tienen efectos transitorios que revierten la media (es decir, la media vuelve a su promedio a largo plazo, que cambia con el tiempo según la determinación). La tendencia).
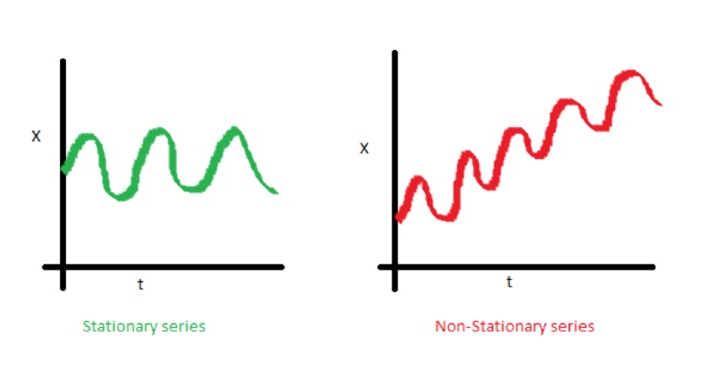
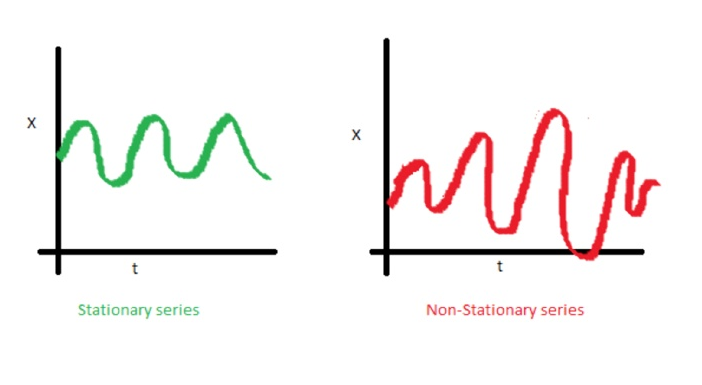
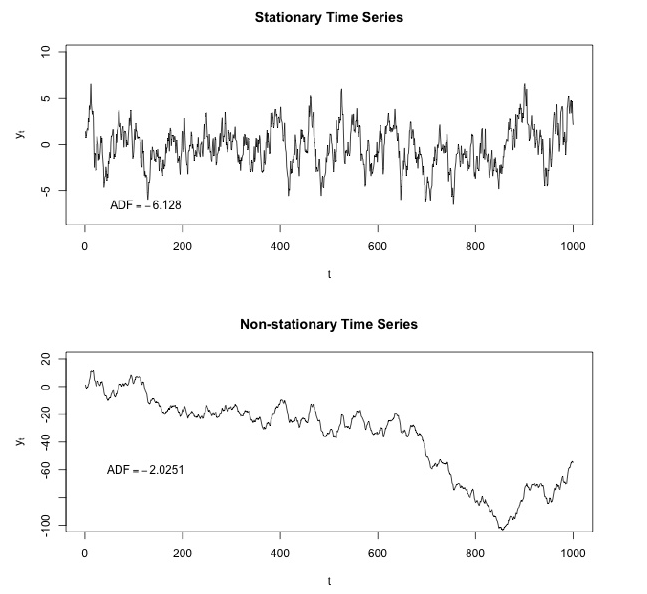
Ejemplos de procesos estacionarios versus no estacionarios
Línea de tendencia
Dispersión
El ruido blanco es un proceso estacionario estocástico que se puede describir utilizando dos parámetros: media y dispersión (varianza). En tiempo discreto, el ruido blanco es una señal discreta cuyas muestras se consideran como una secuencia de variables aleatorias no correlacionadas en serie con media cero y varianza finita.
Si hacemos una proyección sobre el eje y, podemos ver una distribución normal. El ruido blanco es un proceso gaussiano en el tiempo.
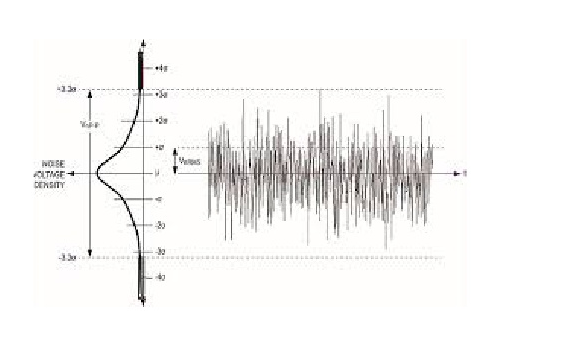
En la teoría de la probabilidad, la distribución normal (o gaussiana) es una distribución de probabilidad continua muy común. Las distribuciones normales son importantes en estadística y a menudo se usan en las ciencias naturales y sociales para representar variables aleatorias de valor real cuyas distribuciones no se conocen. La distribución normal es útil debido al teorema del límite central. En su forma más general, bajo algunas condiciones (que incluyen la varianza finita), establece que los promedios de muestras de observaciones de variables aleatorias extraídas independientemente de distribuciones independientes convergen en la distribución a lo normal, es decir, se distribuyen normalmente cuando el número de observaciones Es suficientemente grande. Las cantidades físicas que se espera que sean la suma de muchos procesos independientes (como los errores de medición) a menudo tienen distribuciones que son casi normales. Además, muchos resultados y métodos (como la propagación de la incertidumbre y el ajuste de parámetros de mínimos cuadrados) pueden derivarse analíticamente en forma explícita cuando las variables relevantes se distribuyen normalmente.
Supongamos que nuestros datos tienen alguna tendencia. Los picos a su alrededor se deben a muchos factores aleatorios que afectan nuestros datos. Por ejemplo, la cantidad de solicitudes atendidas se describe utilizando este enfoque muy bien. Recolección de basura, errores de caché, paginación por sistema operativo, muchas cosas afectan el tiempo particular de respuesta servida. Tomemos una porción de media hora de nuestros datos, de 2017–08–27 12:00 a 12:30. Podemos ver que estos datos tienen una tendencia y algunas oscilaciones.
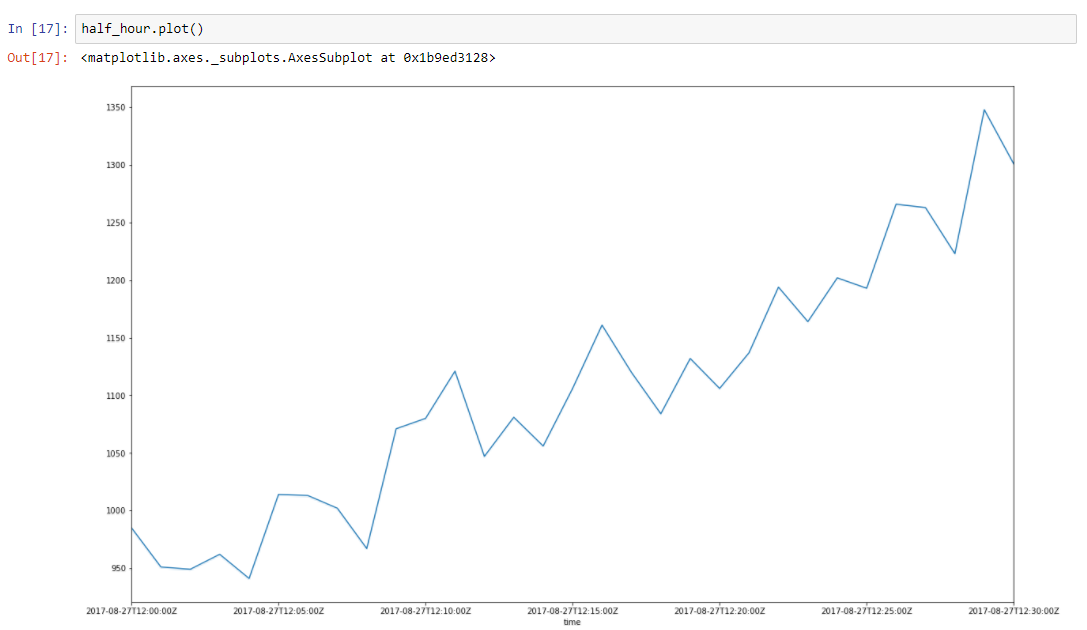
Construyamos una línea de regresión para definir la pendiente de esta línea de tendencia.
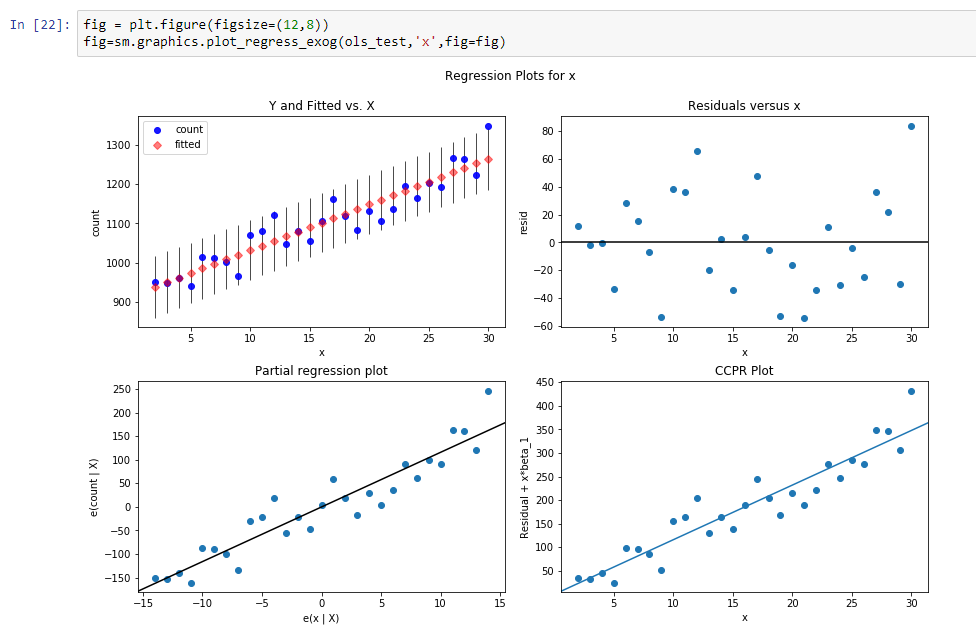
Los resultados de esta regresión son:
const 916.269951dy / dx 11.599507Los resultados significan que const es un nivel para esta línea de tendencia, y dy / dx es una línea de pendiente que define qué tan rápido crece el nivel según el tiempo.
Entonces, en realidad, reducimos la dimensión de los datos de 31 parámetros a 2 parámetros. Si restamos de nuestros datos iniciales nuestros valores de función de regresión, veremos el proceso, que parece un proceso estocástico estacionario.
Entonces, después de la resta, podemos ver que la tendencia ha desaparecido y podemos suponer que el proceso es estocástico en este rango. Pero cómo podemos estar seguros.

Hagamos
Dickey - Prueba más completa .
Dickey: Fuller prueba la hipótesis nula de que las series temporales tienen raíz y también son estacionarias, o rechaza esta hipótesis. Si hacemos la prueba Dickey-Fuller en nuestro segmento inicial, obtendremos
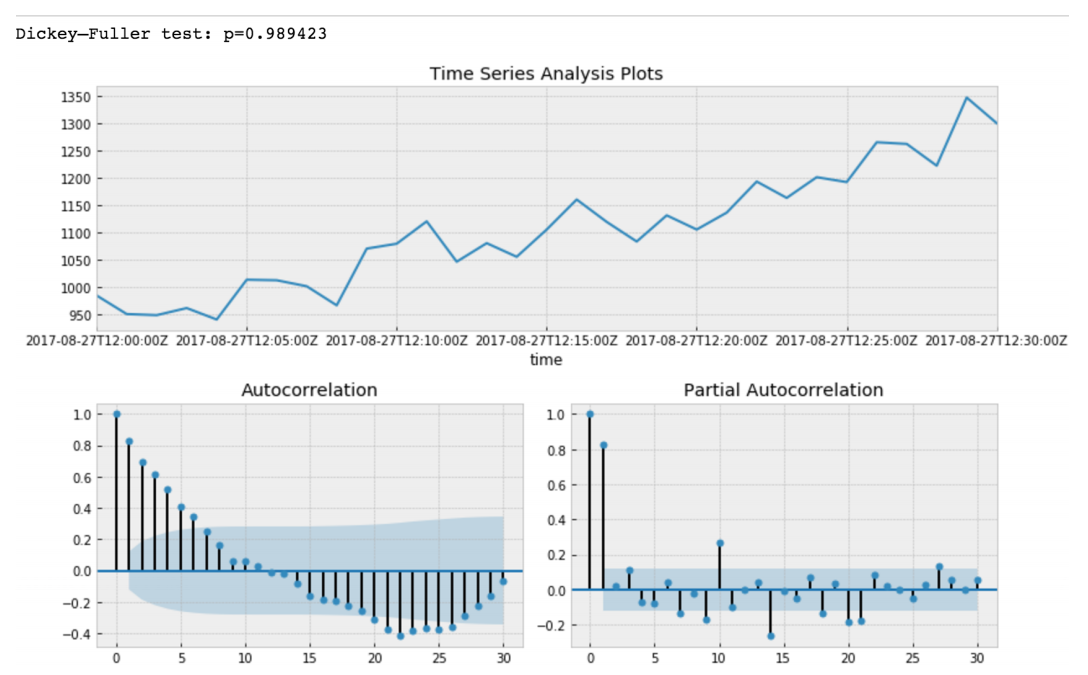
El valor de la prueba Dickey-Fuller rechaza la hipótesis nula con una gran confianza. Por lo tanto, nuestro segmento de series de tiempo no es estacionario. Y podemos ver que la función de autocorrelación muestra autocorrelaciones ocultas.
Después de restar nuestro modelo de regresión de los datos iniciales.

Aquí podemos ver que el valor de la Prueba Dickey-Fuller es realmente pequeño y no rechazamos una hipótesis nula sobre la no estacionariedad de nuestro segmento de series de tiempo. También la función de autocorrelación se ve bien.
Por lo tanto, hemos realizado alguna transformación de nuestros datos y podemos rotar nuestros datos de acuerdo con nuestra pendiente de nuestra línea de tendencia.
Regresión segmentada de los datos.
La regresión segmentada , también conocida como
regresión por partes o “regresión de palo roto”, es un método en el análisis de regresión en el que la variable independiente se divide en intervalos y se ajusta un segmento de línea separado a cada intervalo. El análisis de regresión segmentada también se puede realizar en datos multivariados al dividir las diversas variables independientes. La regresión segmentada es útil cuando las variables independientes, agrupadas en diferentes grupos, exhiben diferentes relaciones entre las variables en estas regiones. Los límites entre los segmentos son puntos de interrupción.
En realidad, nuestra pendiente es una derivada discreta de nuestras series temporales no estacionarias debido al intervalo constante de nuestros puntos métricos que no podemos tener en cuenta dx. Por lo tanto, podemos aproximar nuestros datos como una función por partes que se calcula utilizando derivadas discretas de tendencias de regresión de series de tiempo.

Arriba hay un segmento de datos del 26 al 08-2017 00.00 hasta las 08.00
Parece que hay una autocorrelación lineal para cada segmento y si encontramos una línea de regresión para cada segmento podemos construir un modelo de nuestros segmentos de tiempo utilizando los supuestos que hicimos.
Como resultado, tendremos datos que se describen utilizando una cantidad mínima de parámetros que es favorable debido a una mejor generalización. La dimensión Vapnik - Chervonenkis debe ser lo más pequeña posible para una buena generalización.
En la teoría Vapnik - Chervonenkis, la dimensión VC (para la dimensión Vapnik - Chervonenkis) es una medida de la capacidad (complejidad, poder expresivo, riqueza o flexibilidad) de un espacio de funciones que se puede aprender mediante un algoritmo de clasificación estadística. Se define como la cardinalidad del mayor conjunto de puntos que el algoritmo puede destruir. Originalmente fue definido por Vladimir Vapnik y Alexey Chervonenkis.
Formalmente, la capacidad de un modelo de clasificación está relacionada con lo complicado que puede ser. Por ejemplo, considere el umbral de un polinomio de alto grado: si el polinomio evalúa por encima de cero, ese punto se clasifica como positivo, de lo contrario, como negativo. Un polinomio de alto grado puede ser ondulado, por lo que puede ajustarse bien a un conjunto dado de puntos de entrenamiento. Pero uno puede esperar que el clasificador cometa errores en otros puntos, porque es demasiado ondulante. Tal polinomio tiene una alta capacidad. Una alternativa mucho más simple es poner en umbral una función lineal. Es posible que esta función no se ajuste bien al conjunto de entrenamiento, ya que tiene una capacidad baja.
Como resultado, hemos aproximado nuestros intervalos de horas usando regresión segmentada.
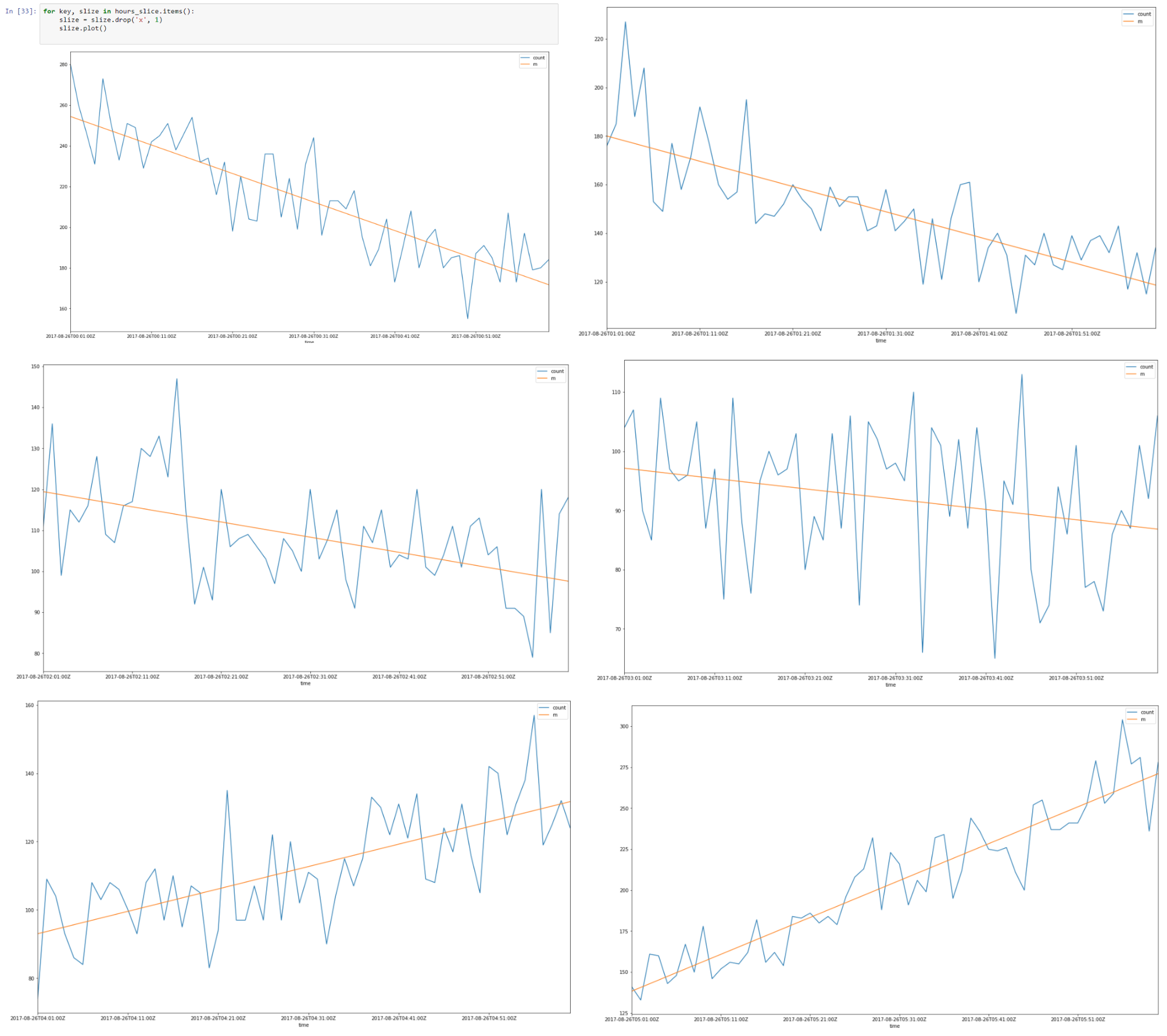
Poniendo todas las rebanadas de 8 horas

Y hacerlo estacionario estocástico restando el modelo de regresión.
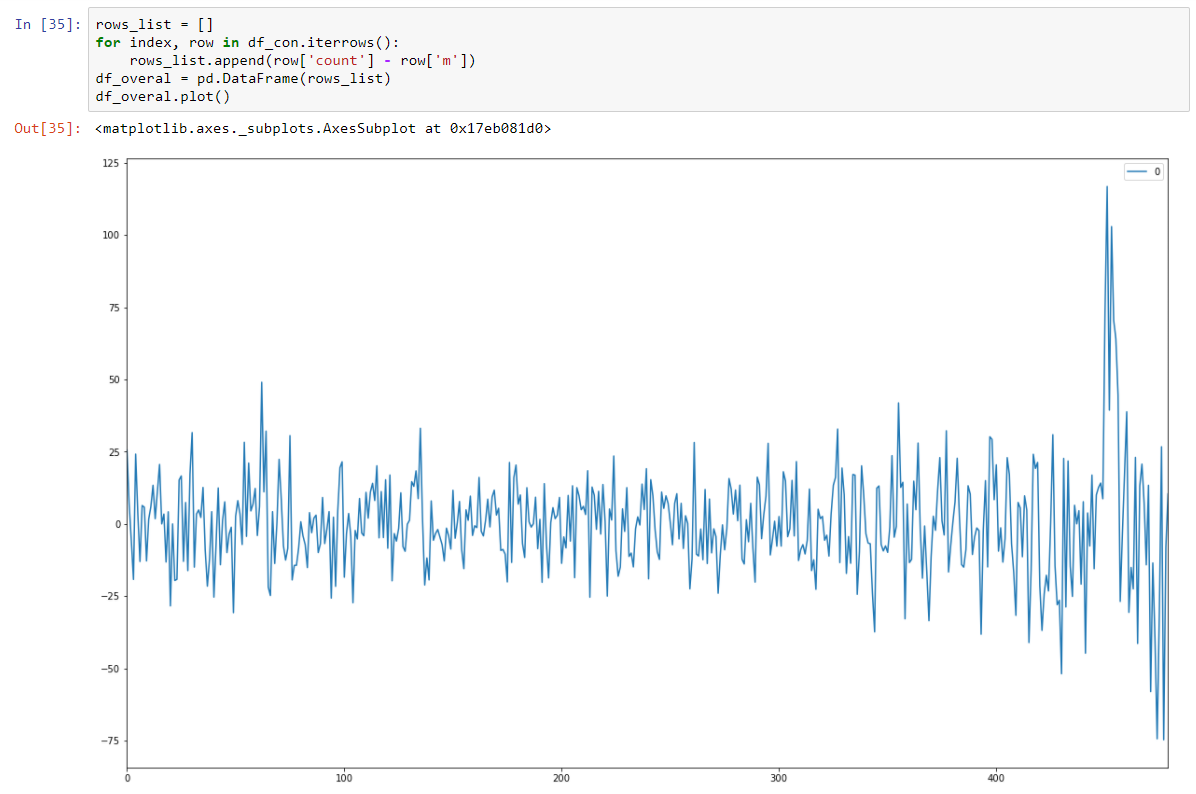
Y nuestra prueba de Dickey-Fuller en estacionaria muestra con gran confianza que transformamos nuestros datos en series estacionarias.
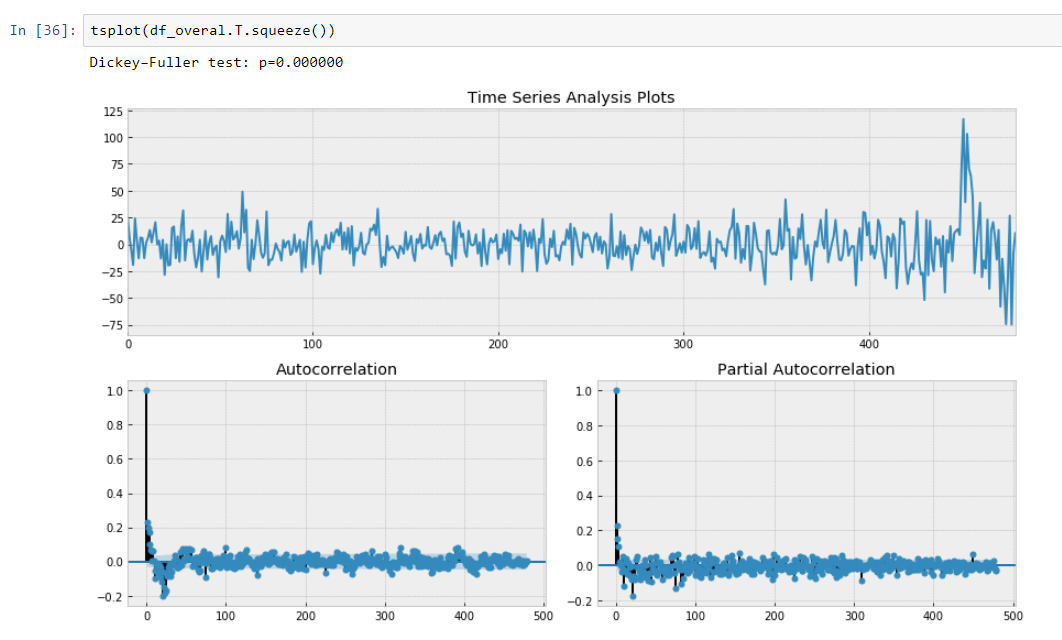
Entonces tenemos un modelo de predicción que describe nuestros datos de series de tiempo. ¡Hemos reducido la dimensionalidad de nuestros datos 15/30 veces más pequeña!
En realidad, deberíamos devolver la media de la predicción de nuestro modelo y transformarla nuevamente usando el nivel y la pendiente para un segmento en particular. Minimizará la suma de los errores al cuadrado para la predicción de nuestros modelos.
Pero también debemos almacenar la varianza porque el aumento en la varianza podría conducir a la presencia de nuevos factores desconocidos y, como sabemos por el conocimiento del dominio, es así.
Por lo tanto, los cambios rápidos en la variación también deberían ser alertados.
Queremos usar el modelo ARIMA también, pero un enfoque más general es mejor, y planeamos comparar este modelo y el ARIMA estándar para obtener mejores resultados. Veamos nuestra serie de tiempo (el verde son las variaciones de varianza en los valores atípicos)