El enunciado del problema

Estaba navegando por Internet el otro día y una cosa bastante curiosa me llamó la atención: el motor de Mendocino . Es un rotor de cojinete de muy baja fricción: el original tenía un cilindro de vidrio colgando de dos agujas, pero los modernos usan suspensión magnética. Es un motor sin escobillas: el rotor tiene baterías solares conectadas, que generan corriente para las bobinas envueltas alrededor del rotor. El rotor gira en un campo magnético fijo, las baterías solares quedan expuestas a la fuente de luz una tras otra. Es una solución bastante elegante que es muy posible recrear en casa.

Aquí está el video que explica cómo funciona (en ruso):


Pero este video tenía otra curiosidad aún más fuerte que el motor en sí. En la descripción del video, Dmitry Korzhevsky escribe: “¡NO PUEDES reemplazar el soporte lateral con un imán! ¡No me preguntes más sobre esto!

Exención de responsabilidad: No soy un experto en física y puedo estar muy equivocado en algunas cosas, por lo que las correcciones son bienvenidas.



Analicemos una vez más cómo funciona el sistema de suspensión magnética del rotor. Si tomamos dos imanes, entonces la isolina potencial se ve así, dependiendo de la distancia entre los imanes:



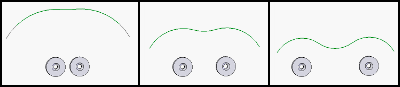
Entonces, colocamos dos imanes fijos en un estator. El imán colocado en el eje del rotor no querrá moverse lateralmente, ya que la isolina potencial tiene un cierto punto mínimo local. En cambio, desearía aparecer a lo largo del eje del rotor. Hacemos dos de estos sistemas y al final, el eje del rotor es estable radialmente, pero es inestable lateralmente. Lo arreglamos inclinando el rotor contra una pared de vidrio y listo, tenemos un rodamiento de baja fricción.

Pero la pared de cristal es un poco ... no estéticamente agradable, ¿no? Es lógico que quisiéramos suspender el rotor en el aire por completo, sin muletas mecánicas como esta. Y evidentemente, Dmitry también fue bombardeado con la misma pregunta, por lo que tuvo que señalar en la descripción que es imposible. Y apuesto a que Dmitry no es el único que se cansó de esto.

Veamos esto, cito:

¿Qué pasaría si los imanes base estuvieran espaciados y orientados como en este dibujo? ¿Le daría estabilidad en el plano axial y eliminaría el requisito del espejo?

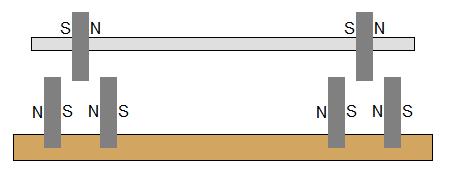
O aquí , cito:

En un motor Mendocino, ¿por qué un lado flota libre mientras que el otro tiene una punta en la pared? Sé que la pregunta puede sonar trivial, pero he ideado la idea de por qué no usar los mismos imanes que se usan para levitar como una fuerza contraria en ambos lados del eje. Adjunté un jpg muy aproximado de lo que quiero decir. Me refiero a los imanes verdes al final de los ejes. ¿Hay alguna teoría o ley que lo impida?

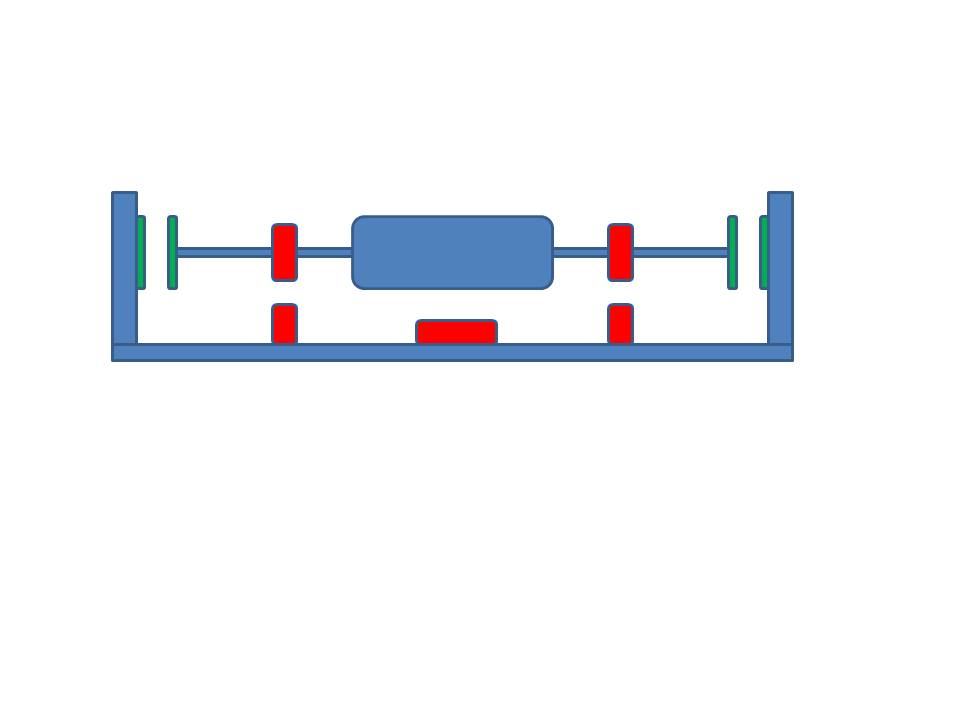
Podemos ver que muchas personas en todo el mundo quieren deshacerse de esta parte mecánica indecorosa. No estaba prestando mucha atención en mis días de escuela, por lo que no era del todo obvio para mí por qué un sistema de suspensión magnética completamente estable no era factible. Un día en el almuerzo le hice esa pregunta a mi supervisor, un científico de fama mundial (en matemáticas aplicadas, no en física): "¿Por qué es imposible?". Y sabes qué, ¡él tampoco lo sabía!

Los foros publicados anteriormente tampoco proporcionaron una respuesta adecuada a esa pregunta. En el mejor de los casos, alguien se refirió a algo llamado el teorema de Earnshaw , que no se presta a la comprensión a primera vista. Establece que: una colección de cargas puntuales no puede mantenerse en una configuración estable de equilibrio estacionario únicamente por la interacción electrostática de las cargas. ¿Lo entendiste? Ciertamente no lo hice. Digamos que puedo aceptar el hecho de que estamos hablando de cargos y no de imanes. Entonces que?

Primera ilustración

Cuando no puedo entender algo, tiendo a dibujarlo. Vamos a ilustrar esto en 2D, por simplicidad. Imagine cuatro cargos fijos, colocados en un patrón cuadrado, más un cargo gratuito en el centro. Así:



¿No está la carga gratuita en equilibrio, entonces? No importa dónde se mueva, se acerca a una de las cargas fijas, lo que aumenta la fuerza de empuje. Intentemos dibujar un mapa de la energía potencial de una carga gratuita. Perdí muchas clases de física en la escuela, así que mi depósito de conocimiento allí es Wikipedia. Entonces, si solo tiene una carga fija, entonces crea un potencial electrostático en el campo que lo rodea:

La ecuación para el potencial electrostático (o potencial de Coulomb) de una carga puntual en el vacío:

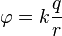
En todos mis experimentos mentales, todos los coeficientes son 0 o 1. Por lo tanto, la carga q es 1, y la k desconocida también es 1. Eso significa que una carga fija crea energía potencial medida como 1 / r, donde r es la distancia a la carga

En nuestro caso, la energía potencial de la carga gratuita dentro del campo de la carga fija también es igual a 1 / r. (para ser justos, la energía es igual a k * q1 * q2 / r, pero elegimos los coeficientes para facilitar los cálculos). Para cargas múltiples, simplemente sumamos todos los potenciales.

Dibujemos un mapa de energía potencial de nuestra carga gratuita. Yo uso salvia para esto:

var('x,y') def unit_potential(a,b,x,y): return 1/(sqrt((xa)^2 + (yb)^2)) def system_potential(x,y): return unit_potential(1,1,x,y)+unit_potential(-1,1,x,y)+unit_potential(1,-1,x,y)+unit_potential(-1,-1,x,y) contour_plot(system_potential(x,y), (x, -2, 2), (y, -2, 2), cmap='hsv', contours=30, region=5-system_potential(x,y), figsize=12, colorbar=True) 

Ahí está nuestro mapa. Los puntos blancos (perforados) es donde la energía potencial se vuelve infinita:



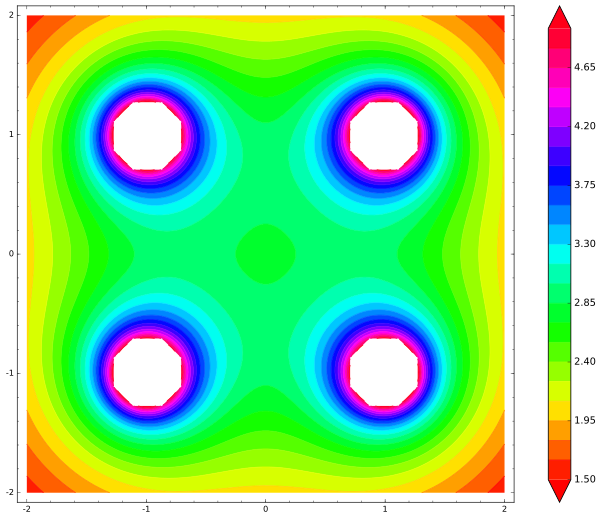
Claramente vemos el mínimo local de energía en el centro. Donde quiera que se mueva la carga central, la energía aumentará, por lo que pequeñas perturbaciones la obligarán a volver al centro, el punto de equilibrio estable. ¿Se equivocó Earnshaw, entonces? No, no lo estaba, solo dibujé la ilustración incorrectamente. Y ese es un error común entre las personas que hacen esa pregunta. Detente unos minutos y adivina: ¿qué me perdí?

De hecho, en este caso, el error fue que en un espacio bidimensional, la carga fija crea energía potencial medida como -ln r, donde r es la distancia a la carga, y no 1 / r. Solo tome mi palabra por el momento y permítame corregir la ecuación sin explicar mucho. El código correcto se ve así:

 var('x,y') def unit_potential(a,b,x,y): return -ln(sqrt((xa)^2 + (yb)^2)) def system_potential(x,y): return unit_potential(1,1,x,y)+unit_potential(-1,1,x,y)+unit_potential(1,-1,x,y)+unit_potential(-1,-1,x,y) contour_plot(system_potential(x,y), (x, -2, 2), (y, -2, 2), cmap='hsv', contours=30, region=5-system_potential(x,y), figsize=12, colorbar=True) 

Y este es el mapa que produce:



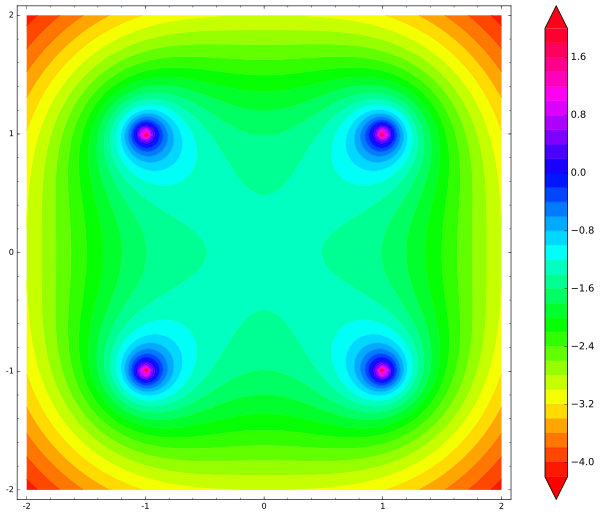
Tenga en cuenta que no hay un mínimo local en ninguna parte. El centro es el punto de silla de montar, o el punto de equilibrio inestable . Tan pronto como la carga gratuita se aleje incluso una micra del centro, inevitablemente saldrá volando del sistema, acelerando en el camino,

Espera un segundo, ¿qué acabas de hacer con la ecuación?

Inicialmente, cuando me di cuenta de que mis cálculos eran totalmente contrarios al teorema de Earnshaw, me di cuenta de que había cometido un error en alguna parte. Es más fácil rastrear mis pasos desde el principio. Respiré hondo y fui a leer sobre las ecuaciones de Maxwell . Nuevamente, no era demasiado bueno en la escuela: no en las calificaciones (éstas eran excelentes), sino en la cantidad de conocimiento que le quité. Por ejemplo, inmediatamente olvidé las ecuaciones de Maxwell, ya que en la universidad y más allá no tuve que trabajar con ellas.

¡Resulta que son bastante simples, especialmente si solo estamos hablando de leyes electrostáticas! Hay cuatro ecuaciones de Maxwell, una para cada una de estas leyes:

• La ley de Gauss, la necesitaremos más tarde. En resumen, es una ley de conservación: la energía no se puede crear de la nada, ni se puede destruir.
• La ley de Gauss para campos magnéticos, que es esencialmente la misma cosa. Y aún no entramos en campos magnéticos, ya que solo estamos hablando de partículas cargadas. Omita esa ley.
• La ley de Faraday: los imanes en movimiento crean un campo eléctrico. Eso es interesante, lo veremos más tarde.
• La ley de Amper: mover un campo eléctrico crea un campo magnético. Inútil para nuestros propósitos.

Entonces, estas cuatro leyes unen dos vectores E y B, campos eléctricos y magnéticos. Estos vectores son funciones con cuatro argumentos (x, y, z, t) y cada cuatro argumentos se yuxtaponen contra un vector tridimensional. No estamos tan interesados ​​en los campos magnéticos, así que echemos un vistazo a los campos eléctricos, o E (x, y, z, t). No olvides que estamos en el ámbito electrostático, por lo que E es constante a lo largo del tiempo. Puedes imaginar este vector como un río, donde en cada punto decimos dónde y qué tan rápido va el agua.

La ley de Faraday establece que un campo E constante en el tiempo (estamos hablando de electrostática allí) no tiene ningún rizo .

¿Cómo se conecta el potencial electrostático a los campos eléctricos? Simple: si el campo E no tiene rizos (como es el caso allí), entonces podemos crearlo de una manera que (volviendo al ejemplo del río), cubierto por una capa de agua de 1 metro (¡a todas las alturas! ) y "liberar: esto, la velocidad y la dirección del flujo de agua crearían el campo E". O, en términos matemáticos, es posible encontrar una función u escalar, cuyo gradiente es igual al campo E.

La ley de Gauss establece: tomar un pequeño barrio. Si no aplicamos cargos deliberadamente, entonces la cantidad de "agua" que fluye hacia el vecindario es igual a la cantidad que fluye hacia afuera. Si queremos sonar inteligentes, la divergencia del campo E es cero.

Recuerde: el campo E es una derivada de la función escalar u. Si su divergencia es cero, significa que el laplaciano de u es cero. Laplaciano es una palabra inteligente para la "curvatura" de la función. Si hablamos de funciones de una variable, el laplaciano es simplemente la segunda derivada. En funciones de dos variables, el laplaciano es la suma de dos derivadas. Si es igual a cero, entonces la curvatura en una dirección debe ser cancelada por la curvatura en la otra dirección. Es decir, las patatas fritas pueden existir:



Pero la función cero-laplaciana no tiene mínimos (o máximos) locales, lo que significa que las patatas fritas están permitidas, pero las colinas no lo son:



Imagine sumergir un círculo de alambre (curvado) en agua jabonosa. La película de jabón luego forma una superficie cero-laplaciana:



Será la llamada "superficie mínima". La película de jabón intenta ser lo más pequeña posible, por lo que es lógico que si tuviera un cierto máximo local, tendríamos una película más pequeña al suavizarla, por lo que no hay ninguna. Entonces, el potencial electrostático es una especie de superficie mínima que no tiene máximos locales (siempre que no hayamos colocado cargas allí deliberadamente).

La función 1 / r tiene un cero laplaciano en tres dimensiones, ¡pero no en dos! Si queremos dibujar ejemplos bidimensionales, necesitaríamos resolver un problema de Dirichlet : para 2D, es -ln r.

Usar la fórmula de los cuadrados inversos en el espacio de 1 o 2 dimensiones corresponde a restringir el movimiento de las cargas a lo largo de los ejes restantes de alguna otra manera. En este caso, es obvio que es posible hacer una configuración estable: simplemente tome un tubo de cartón, colóquelo verticalmente y baje su imán. Entonces es posible colocar allí un imán más que estará en equilibrio: horizontalmente está restringido por el tubo (es decir, está en un espacio unidimensional), y en una fuerza vertical de gravedad y la repulsión de un imán se contrarrestan. El teorema de Earnshaw debe aplicarse con la ley de los cuadrados inversos, pero en 3d, o en el espacio de cualquier dimensión, pero con el potencial correspondiente. "Correspondiente" significa el obtenido de las ecuaciones de Maxwell.

El teorema de Earnshaw y sus consecuencias.

Entonces, volviendo a nuestro ejemplo con una partícula cargada libre. El potencial de un campo electrostático no tiene mínimos locales y, como resultado, la energía potencial de la partícula no tiene mínimos locales. Entonces, una partícula no puede alcanzar un equilibrio estable en un campo estático. Felicitaciones, acabamos de probar el teorema de Earnshaw. ¿Pero qué hay de los sistemas más complicados? ¿Cómo aplicar el teorema allí?

Aquí hay otro ejemplo que, según mi jefe, debería haber refutado el teorema de Earnshaw. Arreglemos dos cargas y creemos un cuerpo móvil que consista en un palo sin estirar sin peso con cargas en ambos extremos:



Intuitivamente, si movemos la palanca ligeramente hacia la izquierda o hacia la derecha, entonces uno de los extremos se acercaría a las cargas fijas, lo que lo alejará y devolverá la palanca a la posición original. Entonces, ¿cuál es el problema? Dibujemos un mapa del potencial electrostático de dos cargas fijas:

 var('x,y') def unit_potential(a,b,x,y): return -ln(sqrt((xa)^2 + (yb)^2)) def system_potential(x,y): return unit_potential(0,1,x,y)+unit_potential(0,-1,x,y) contour_plot(system_potential(x,y), (x, -2, 2), (y, -2, 2), cmap='hsv', contours=30, figsize=12, colorbar=True) 

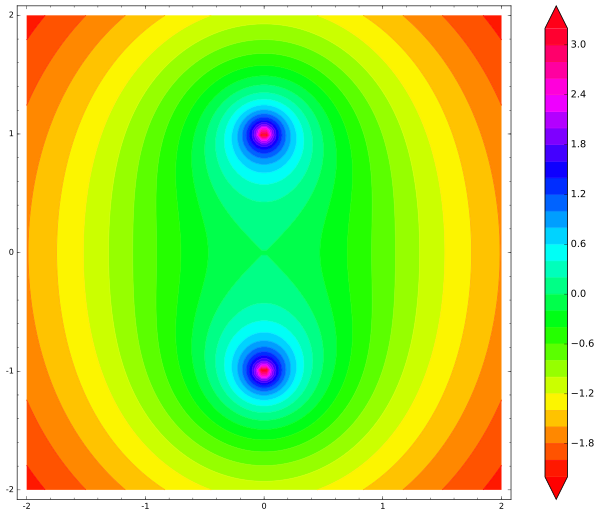
¿Cómo ilustramos la energía potencial de nuestro palo? El palo tiene tres grados de libertad (dos para movimiento y uno para rotación), por lo que el gráfico sería de cuatro dimensiones. Ignoremos la rotación por ahora y solo dejemos que el palo se mueva de lado a lado. Arreglamos un punto en un palo (por ejemplo, su centro) y dibujamos el mapa de la energía potencial del palo para su centro. En este caso, la energía potencial total del palo es la suma de las energías potenciales de sus cargas en ambos extremos:

 var('x,y') def unit_potential(a,b,x,y): return -ln(sqrt((xa)^2 + (yb)^2)) def system_potential(x,y): return unit_potential(0,1,x,y)+unit_potential(0,-1,x,y) def energy(x,y): return system_potential(x+2,y)+system_potential(x-2,y) contour_plot(energy(x,y), (x, -3, 3), (y, -2, 2), cmap='hsv', contours=30, figsize=12, colorbar=True) 

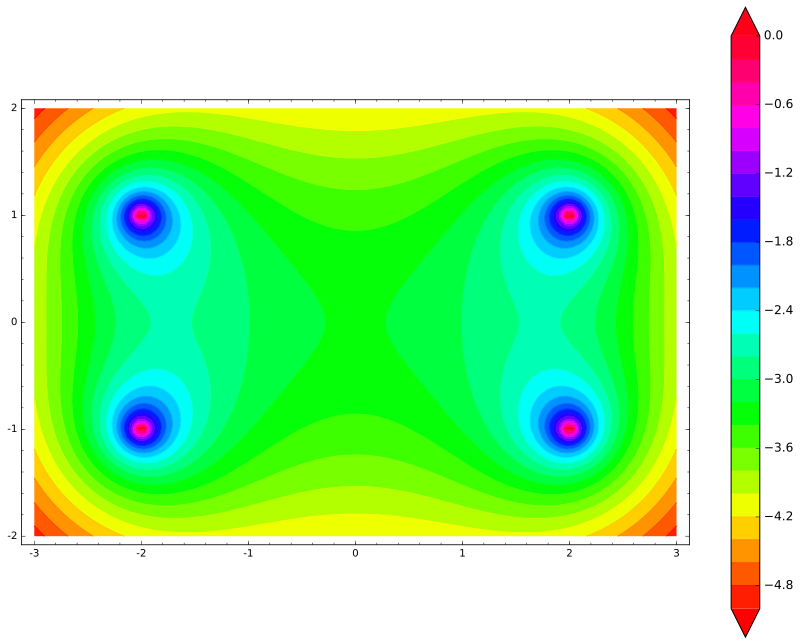
Entonces, la energía del palo tiene cuatro picos (cada extremo puede golpear cada una de las dos cargas). Como se esperaba, el palo no se movería horizontalmente; en cambio, ¡se movería verticalmente!

Es lógico, ya que ¿cómo obtuvimos la energía? Sumamos energías potenciales de cada carga. Sabemos que la energía potencial de cada carga es una función cero-laplaciana. Su suma, por lo tanto, también tiene un cero laplaciano. Por lo tanto, la energía potencial de cualquier cuerpo cargado (¡no solo nuestro palo!) ¡No puede tener mínimos en un campo eléctrico estático!

Conclusión

Las imágenes intuitivas de campos magnéticos y eléctricos de personas que no trabajan estrechamente en física pueden ser engañosas. Nuestro cerebro nos engaña haciendo imágenes de mínimos de energía. Desafortunadamente, no es el caso, y crear un motor Mendocino sin soporte mecánico es muy difícil, si no imposible.

¿Qué lagunas hay para explotar? El teorema de Earnshaw (si lo aplicamos a los imanes) solo se aplica a los sistemas de imanes fijos y estáticos .

1. Podemos crear un campo magnético dinámico.
2. El diamagnetismo y los superconductores tampoco caen bajo el teorema de Earnshaw.
3. Los cuerpos móviles (y específicamente, rotativos) no se discuten allí en absoluto, siendo el levitrón el ejemplo más famoso.

No, no es inútil. Claro, usar cualquiera de estas lagunas mataría la estética de un motor de Mendocino, ¡pero la magia de una cosa de metal que levita libremente triunfaría sobre todo eso!

Última nota: fue el teorema de Earnshaw el que demostró la inexistencia de materia sólida, por lo tanto, refutando el modelo aceptado de un átomo, lo que condujo al modelo de átomo "planetario".