Les barres de Zhenya et Luke - un outil multiplicateur de la fin du XIXe siècle
Cet article est consacré à un outil auxiliaire de multiplication, les barres proposées en 1885 par l'ingénieur des chemins de fer Eugène (sic) et un employé du Musée des Arts et Métiers de Paris Eduard Luke (sic) [1].La translittération des noms des inventeurs diffère selon les sources, je cite donc en latin un certain nombre d'options (que j'ai dû google): Genaille (Zhenya, Zhenya, Zhenya, Zhenail), Lucas (Luca, Luc, Lucas).Les barreaux de Zhenya et Luke étaient plus pratiques que les baguettes de Neper qui les ont précédés, et pourraient bien rivaliser avec les barreaux modernes de Joffe (construits sur le théorème de Slonimsky).Il n'y a pratiquement aucune information sur ce produit dans Runet. L'autre jour, j'ai soudainement googlé un article en allemand qui m'a aidé à entrer dans le principe des bars. Non limité à l'article, j'ai restitué l'apparence de la surface de travail des barres à partir des images en vue de certaines d'entre elles et en me concentrant sur le principe de leur action. Les matériaux trouvés plus tard sur le même site ont confirmé l'exactitude de ma reconstruction.But de la rédaction d'un article
Cet article s'adresse à ceux qui, comme moi, s'intéressent à l'histoire de la technologie informatique.Dans RuNet, je n'ai rien trouvé de raisonnable sur les bars de Zhenai et Luc (Genaille & Lucas). Le site Internet en langue allemande , sur lequel a été trouvé un article avec sa description, a permis de comprendre le principe de fonctionnement de cet outil de comptage .Pourquoi Habr est sélectionné comme emplacement de l'article
L'article est consacré, bien qu'ancien, mais toujours informatique. Par conséquent, convient à Habr sur un sujet.Habr est bien indexé, et je veux qu'il soit facile pour quiconque est intéressé par cet outil de comptage de trouver des informations à ce sujet.Description et fonction du produit
Les barres de Zhenya et Luke, ainsi que d'autres produits similaires, sont conçues pour obtenir rapidement le produit d'un numéro à plusieurs chiffres avec un numéro à un seul chiffre.L'outil multiplicateur est un ensemble de 11 barres. Chaque barre possède une échelle numérique sur laquelle se trouve le résultat. L'échelle est divisée en 8 parties, correspondant à une multiplication par des nombres de 2 à 9. Une barre sert d'indice - les parties de son échelle sont signées par les nombres 2 ... 9 - ce sont les valeurs d'un facteur à un chiffre, et son échelle elle-même est conçue pour lire le plus haut niveau du travail. Les barres restantes sont numérotées de 0 à 9 et sont conçues pour multiplier les nombres correspondants. En eux, à côté de l'échelle, il y a un triangle, dont le côté droit limite l'échelle numérique à gauche, et le sommet gauche est sur le bord gauche de la barre - lorsque les barres sont empilées ensemble, cela indique la position de la prochaine décharge du produit sur la barre suivante.









 Une petite analyse: il est facile de voir que chaque partie de l'échelle de chaque barre commence par un chiffre égal à la valeur de la catégorie d'unités du produit du nombre de la barre par le numéro de la partie de l'échelle. Par exemple, dans la mesure 8, le fragment 9 commence par le nombre 2 (8 * 9 = 72). La longueur de chaque partie de l'échelle est égale à la valeur d'un facteur à un chiffre - ce qui est naturel, car lors de la multiplication d'un nombre par un facteur à un chiffre, le chiffre le plus élevé du produit est inférieur à ce facteur, c'est-à-dire multipliée, par exemple par 5, la valeur transférée au chiffre suivant ne dépassera jamais 4, multipliée par 9, respectivement 8, etc. La quantité de décalage des chiffres vers le bas depuis le début de l'échelle est égale à la valeur du transfert du bit le moins significatif. Il s'avère que la position du sommet gauche du triangle noir correspond à la valeur du deuxième chiffre du produit du numéro de barre par un facteur à un chiffre, auquel un nombre est ajouté,transféré de l'ordre inférieur.Afin de multiplier un nombre à plusieurs chiffres par un nombre à un seul chiffre, vous devez ajouter les barres avec les nombres correspondant aux chiffres des chiffres et attacher une barre avec un indice sur la gauche. Ensuite, dans chaque partie de l'échelle, il sera possible de considérer les produits de ce numéro par le numéro à un chiffre correspondant. La décharge des unités est le premier chiffre de la partie souhaitée de l'échelle, et chaque décharge suivante nous indiquera le sommet gauche du triangle, dont le côté droit sert de bord gauche à la cellule de la décharge précédente.Par exemple, prenez le nombre 7519. Mettons ensemble une barre avec un indice et les barres 7, 5, 1 et 9. Le diagramme est illustré dans l'image ci-dessous.
Une petite analyse: il est facile de voir que chaque partie de l'échelle de chaque barre commence par un chiffre égal à la valeur de la catégorie d'unités du produit du nombre de la barre par le numéro de la partie de l'échelle. Par exemple, dans la mesure 8, le fragment 9 commence par le nombre 2 (8 * 9 = 72). La longueur de chaque partie de l'échelle est égale à la valeur d'un facteur à un chiffre - ce qui est naturel, car lors de la multiplication d'un nombre par un facteur à un chiffre, le chiffre le plus élevé du produit est inférieur à ce facteur, c'est-à-dire multipliée, par exemple par 5, la valeur transférée au chiffre suivant ne dépassera jamais 4, multipliée par 9, respectivement 8, etc. La quantité de décalage des chiffres vers le bas depuis le début de l'échelle est égale à la valeur du transfert du bit le moins significatif. Il s'avère que la position du sommet gauche du triangle noir correspond à la valeur du deuxième chiffre du produit du numéro de barre par un facteur à un chiffre, auquel un nombre est ajouté,transféré de l'ordre inférieur.Afin de multiplier un nombre à plusieurs chiffres par un nombre à un seul chiffre, vous devez ajouter les barres avec les nombres correspondant aux chiffres des chiffres et attacher une barre avec un indice sur la gauche. Ensuite, dans chaque partie de l'échelle, il sera possible de considérer les produits de ce numéro par le numéro à un chiffre correspondant. La décharge des unités est le premier chiffre de la partie souhaitée de l'échelle, et chaque décharge suivante nous indiquera le sommet gauche du triangle, dont le côté droit sert de bord gauche à la cellule de la décharge précédente.Par exemple, prenez le nombre 7519. Mettons ensemble une barre avec un indice et les barres 7, 5, 1 et 9. Le diagramme est illustré dans l'image ci-dessous.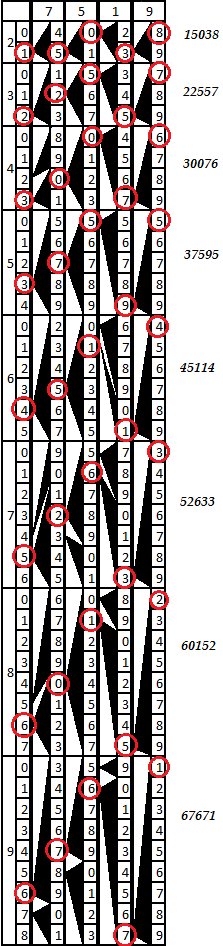 Dans chaque partie du tableau résultant, en suivant les signes du triangle, vous pouvez tracer les catégories d'œuvres de droite à gauche.Le schéma est plus clair que tous les mots. Suivons, par exemple, la multiplication par 9. Au début de la neuvième (dernière) partie de l'échelle de la barre de droite, nous voyons le nombre 1. Le triangle de celui-ci pointe vers le nombre 7 de la barre voisine, de là le triangle pointe vers 6, puis vers 7, et même plus loin vers le numéro 6 sur l'échelle à pointe de barre. À. nous obtenons la valeur 67671 = 7519 * 9.D'autres travaux sont également tracés. Il est facile de vérifier qu'ils sont corrects. Par conséquent, l'outil peut être utilisé.
Dans chaque partie du tableau résultant, en suivant les signes du triangle, vous pouvez tracer les catégories d'œuvres de droite à gauche.Le schéma est plus clair que tous les mots. Suivons, par exemple, la multiplication par 9. Au début de la neuvième (dernière) partie de l'échelle de la barre de droite, nous voyons le nombre 1. Le triangle de celui-ci pointe vers le nombre 7 de la barre voisine, de là le triangle pointe vers 6, puis vers 7, et même plus loin vers le numéro 6 sur l'échelle à pointe de barre. À. nous obtenons la valeur 67671 = 7519 * 9.D'autres travaux sont également tracés. Il est facile de vérifier qu'ils sont corrects. Par conséquent, l'outil peut être utilisé.Spéculations sur le thème de l'apparence
Apokin I.A., Maistrov L.E. dans la source [1], ils écrivent que les barres numériques avaient les quatre surfaces fonctionnelles. Il est logique de supposer que les surfaces ont été utilisées pour dupliquer des échelles, ce qui est nécessaire pour compiler des nombres à plusieurs chiffres avec plusieurs occurrences du même chiffre.En fonction du nombre de côtés de la barre, supposons qu'il y ait quatre jeux complets d'échelles sur 10 barres.Supposons que les échelles sur les barres doivent être disposées de manière à ce que les barres vous permettent de faire n'importe quel nombre à quatre chiffres.Vous pouvez trouver de nombreuses options pour placer des échelles de travail sur des barres qui répondent à cette exigence. Par exemple, prenez deux barres de cinq types ayant respectivement des faces:0,1,2,3;2,3,4,5;4,5,6,7;6,7,8,9;0,1,8,9.Une autre option pour utiliser quatre faces est de placer une échelle sur elles en plusieurs parties et ainsi de réduire la longueur de la barre. Cette option est moins pratique à utiliser, car ne permet pas de voir toutes les œuvres à la fois.L'échelle se compose de 8 parties, d'une longueur allant de 2 à 9. Collectionnez-les en quatre groupes sans perturber l'ordre:2 + 3 + 4 + 5 = 14; 6 + 7 = 13; 8; 9. La longueur la plus longue est 14.S'il est permis de perturber l'ordre, alors les parties de l'échelle sont facilement groupées:2 + 9; 3 + 8; 4 + 7; 6 + 5. Ceux. la longueur de la barre est réduite à 11.Littérature
1. Apokin I.A., Maistrov L.E. "L'histoire de la technologie informatique: des appareils informatiques les plus simples aux systèmes de relais complexes." (Moscou: Maison d'édition Nauka, 1990)2. www.mechrech.infoPS
Une question pour ceux qui connaissent le français: comment diable est-il juste de traduire correctement les noms de Genaille et Lucas?UPD: Merci. Corrigé dans tout l'article sur Zhenai (classe) et Luke (hors classe) Source: https://habr.com/ru/post/fr380549/
All Articles