Le "paradoxe de l'inspection" est partout

Beaucoup de gens connaissent le soi-disant «paradoxe de l'amitié» dans les réseaux sociaux, mentionné pour la première fois dans les travaux scientifiques de 1991, lorsque les réseaux sociaux n'étaient que hors ligne. Ce paradoxe s'applique aux réseaux sociaux modernes sur Internet.

Si vous prenez n'importe quel utilisateur de Facebook et sélectionnez au hasard l'un de ses amis, alors avec une probabilité de 80%, un ami aura plus "d'amis". Les personnes qui ne connaissent pas les statistiques mathématiques sont très contrariées par le fait que presque tous leurs amis réussissent mieux en communication qu'eux-mêmes. Mais il n'y a pas de raison à la dépression: il devrait en être ainsi, conformément à la science et au bon sens.

Le paradoxe de l'amitié est l'une des formes du «paradoxe de l'inspection», qui se retrouve partout et trompe souvent les citadins.

L'essence du paradoxe de l'amitié est que les utilisateurs avec un grand nombre d'amis sont plus susceptibles de tomber dans l'échantillon statistique. Par exemple, selon la Stanford Large Network Dataset Collection , l'utilisateur moyen de Facebook a 42 amis sur un échantillon de 4 000 personnes, et chacun de ces amis a en moyenne 91 amis.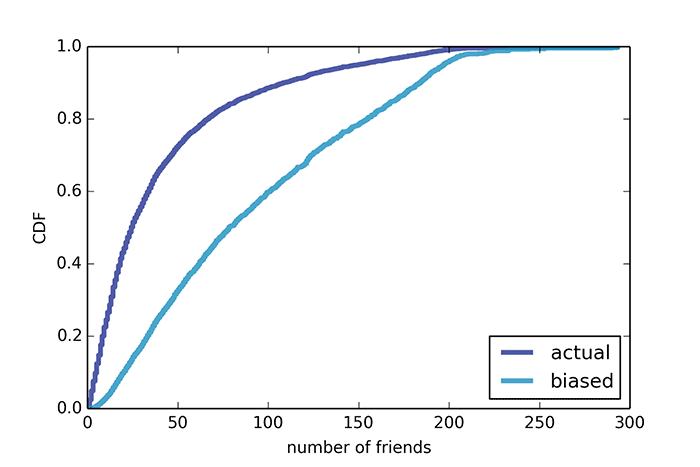



La même chose est observée dans d'autres domaines de recherche.

Par exemple, le paradoxe de la taille des classes. Supposons que nous interrogions les élèves sur le nombre de personnes qui étudient avec eux dans un groupe, puis que nous dérivions la moyenne arithmétique de leurs réponses - et nous obtenons 56 personnes. Mais l'administration universitaire dit que le nombre moyen d'étudiants dans un groupe est de 31. Assez curieusement, personne ne ment et les deux valeurs sont justes. Juste au cours de l'enquête, les élèves de grands groupes sont plus susceptibles de se joindre à l'échantillon, car ils sont en fait plus nombreux. Si nous avons deux groupes de 10 et 100 personnes, 100 répondants sur 110 diront que la taille de leur groupe est de 100 personnes, et seulement 10 personnes diront la taille du groupe 10. La taille moyenne du groupe, selon cette enquête, sera de 92 étudiants.

Cela semble une erreur courante, mais c'est une source de malentendu dans de nombreuses situations réelles. Par exemple, lors de l'analyse du trafic passagers dans les transports publics. Le professeur d'informatique Allen Downey, pour un article dans le Journal of the American Statistical Society, fournit un exemple du temps moyen entre les trains Red Line à Boston. Il a enregistré l'heure d'arrivée de 70 trains entre 17h00 et 18h00.



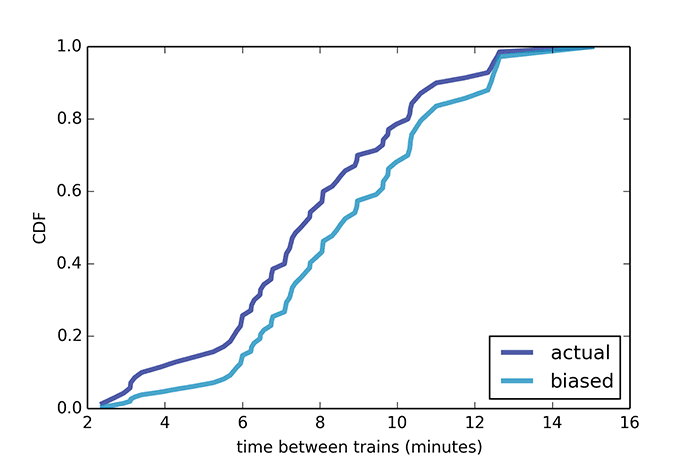L'intervalle minimum entre les trains était de 3 minutes, le maximum - 15 minutes. Selon les données réelles, l'intervalle moyen entre les trains est de 7,8 minutes, c'est-à-dire que le temps d'attente moyen pour un train devrait être d'environ 3,9 minutes. Mais une enquête auprès des passagers montre que le temps d'attente moyen était en fait de 4,4 minutes et l'intervalle entre les trains était de 8,8 minutes, soit 15% de plus.

La raison en est qu'avec un retard plus important dans le train, plus de passagers l'attendent, tandis que les trains arrivant avec un intervalle plus court sont moins encombrés. En conséquence, la plupart des passagers se plaignent de l'écrasement de la voiture et du long temps d'attente pour le train, alors que selon la compagnie, le temps et la charge moyens des voitures sont normaux.

Le même problème avec les vols. La plupart des passagers parlent de salons à cabine complète, tandis que les compagnies aériennes se plaignent de la perte de bénéfices car de nombreux vols volent presque à vide. Les deux ont raison.

Un «paradoxe d'inspection» est observé, par exemple, dans les courses de longue distance ou lorsque vous voyagez en voiture le long de l'autoroute. Dans chacun de ces cas, le participant au mouvement dépasse «trop lentement», et il est dépassé par «trop vite». Cela crée une impression subjective que tous les participants au mouvement sont divisés en trop lent ou trop rapide, mais pas moyen.

Le dernier exemple d'Allen Downey est né après avoir lu Orange - The Hit of the Season, un mémoire de Piper Kerman, qui a passé 13 mois en prison fédérale. Dans l'un des fragments du livre, elle exprime sa surprise devant la longue durée des peines que les détenus purgent. De toute évidence, la fille n'est pas familière avec les lois de la statistique mathématique. Mais conformément au paradoxe de l'inspection, si vous allez en prison à un moment aléatoire et choisissez un prisonnier au hasard, alors avec une probabilité élevée, il est condamné à une longue peine d'emprisonnement. Ce n'est pas une preuve du système carcéral inhumain des États-Unis, mais une simple conclusion du paradoxe de l'inspection.



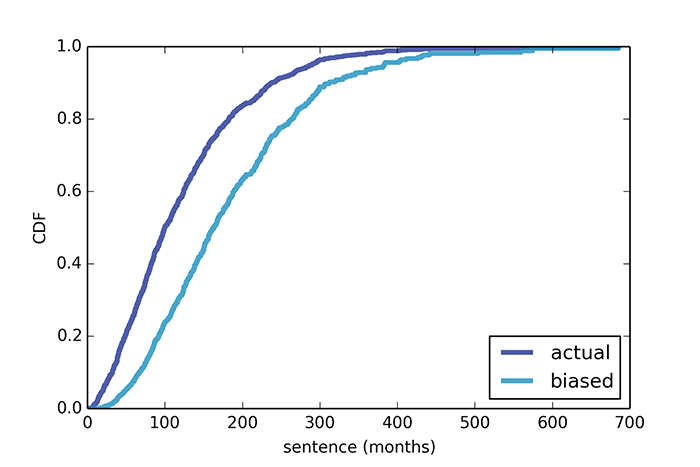Selon les données officielles de la US Sentencing Commission, la durée moyenne est de 121 mois et la «durée moyenne subjective» pour interroger les détenus est de 183 mois.

Même lors des entretiens menés pendant treize mois avec les détenus environnants, comme le montre le calcul, le résultat moyen obtenu ne diffère pas beaucoup de l'enquête initiale unique.



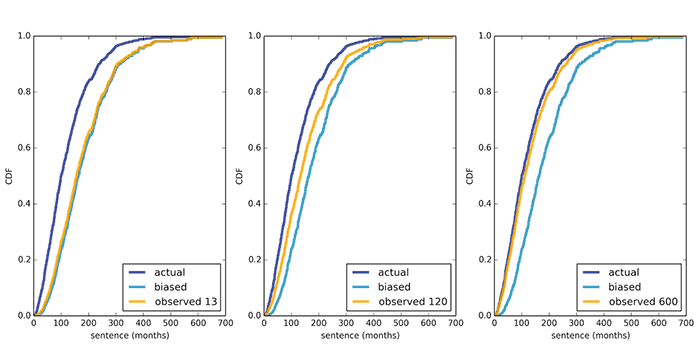Un chiffre plus ou moins objectif peut être obtenu en interrogeant pendant 600 mois ou plus.

Source: https://habr.com/ru/post/fr383787/