Localisation laser, imagerie Doppler et synthèse d'ouverture

La résolution angulaire est la caractéristique la plus importante de tout système télescopique. L'optique affirme que cette résolution est sans ambiguïté liée à la longueur d'onde à laquelle l'observation est effectuée et au diamètre de l'ouverture d'entrée du télescope. Avec de gros diamètres, comme vous le savez, un gros problème. Il est peu probable qu'un télescope soit jamais construit plus que cela .
Une façon d'augmenter considérablement la résolution est la méthode utilisée en radioastronomie et radar pour synthétiser de grandes et très grandes ouvertures. Au millimètre près, la plus grande ouverture - 14 km - devrait être formée par les 66e antennes du projet ALMA au Chili.

Le transfert des méthodes de synthèse d'ouverture vers la région optique, où les longueurs d'onde sont de plusieurs ordres de grandeur plus courtes que celle des radars, est associé au développement de techniques d' hétérodynage laser .

1. Fondements physiques de la formation d'images.

Ce ne sera pas une erreur de dire que l'image d'un appareil optique est formée par diffraction de la lumière à l'ouverture d'entrée, et rien de plus. Regardons l'image de l'objet depuis le centre de l'ouverture. La distribution angulaire de la luminosité de l'image d'une source ponctuelle de lumière infiniment éloignée (comme, en fait, de toute autre) sera la même pour un objectif et un sténopé de diamètre égal. La différence entre un objectif et un sténopé est seulement que l'objectif transfère l'image formée par son ouverture de l'infini à son plan focal. Ou, pour le dire autrement, produit une transformation de phase du front d'onde du plan d'entrée en un front convergent sphériquement. Pour une source ponctuelle distante et une ouverture circulaire, une image est une image Airy bien connue avec des anneaux .

La taille angulaire du disque Airy peut être réduite en principe et, pour ainsi dire, augmenter la résolution ( selon le critère de Rayleigh ) si l'ouverture est fixée de manière spéciale. Il existe une telle distribution de transmission sur le rayon, dans laquelle le disque central peut théoriquement être rendu arbitrairement petit. Cependant, dans ce cas, l'énergie lumineuse est redistribuée le long des anneaux et le contraste de l'image complexe tombe à zéro.

D'un point de vue mathématique, la procédure de génération d'une image de diffraction se réduit à une transformée de Fourier bidimensionnelle à partir du champ lumineux d'entrée (dans l'approximation scalaire, le champ est décrit par une fonction complexe de coordonnées et de temps). Toute image enregistrée par l'œil, l'écran, la matrice ou tout autre récepteur quadratique en intensité n'est rien de plus qu'un spectre d'amplitude bidimensionnelle du limité par le champ lumineux d'ouverture émis par l'objet. Il est facile d'obtenir la même image Airy si vous prenez une matrice carrée des mêmes nombres complexes (simulant un front d'onde plat à partir d'un point éloigné), en «découpant» une «ouverture» ronde, en remettant à zéro les bords et en faisant une transformée de Fourier de la matrice entière.

En bref, si vous enregistrez en quelque sorte le champ (synthétisez l'ouverture) sur une zone suffisamment grande sans perte d'informations d'amplitude et de phase, alors pour obtenir une image, vous pouvez vous passer des miroirs géants des télescopes modernes et des matrices mégapixels, en calculant simplement la transformée de Fourier du tableau de données résultant.

2. Localisation satellite et super résolution.

Nous observerons un objet stabilisé se déplaçant sur la ligne de visée éclairé par une source laser cohérente continue. Le rayonnement réfléchi est enregistré par un photodétecteur hétérodyne à petite ouverture. Enregistrer un signal dans le temps t équivaut à réaliser une ouverture unidimensionnelle de longueur vt, où v est la vitesse tangentielle de l'objet. Il est facile d'évaluer la résolution potentielle d'une telle méthode. Regardons le satellite proche de la Terre dans l'allongement supérieur, volant à une altitude de 500 km à une vitesse de 8 km / s. En 0,1 seconde d'enregistrement du signal, nous obtenons un «télescope unidimensionnel» de 800 mètres de taille, théoriquement capable de visualiser les parties satellites dans le domaine visible en une fraction de millimètre. Pas mal pour une telle distance.

Bien sûr, le signal réfléchi à de telles distances diminue de plusieurs ordres de grandeur. Cependant, la réception hétérodyne (mélange cohérent avec le rayonnement de référence) compense largement cette atténuation. En effet, comme vous le savez, le photocourant de sortie du récepteur dans ce cas est proportionnel au produit des amplitudes du rayonnement de référence et du signal entrant. Nous augmenterons la proportion de rayonnement de référence et amplifierons ainsi l'ensemble du signal.

Vous pouvez regarder de l'autre côté. Le spectre du signal enregistré provenant du photodétecteur est un ensemble de composants Doppler, dont chacun est la somme des contributions de tous les points de l'objet qui ont la même vitesse radiale. La distribution unidimensionnelle des points réfléchissants sur un objet détermine la distribution de fréquence des raies spectrales. Le spectre résultant est essentiellement une «image» unidimensionnelle de l'objet le long de la coordonnée «décalage Doppler». Deux points de notre satellite, situés à 1 mm l'un de l'autre dans un plan perpendiculaire à la ligne de visée, ont une différence de vitesse radiale de l'ordre de 0,01-0,02 mm / s. (Le rapport de cette différence à la vitesse du satellite est égal au rapport de la distance entre les points à la distance au satellite). La différence des fréquences Doppler de ces points pour une longueur d'onde visible de 0,5 µm sera (f = 2V / λ) de l'ordre de 100 Hz.Le spectre (image Doppler) de l'ensemble du microsatellite, disons de 10 cm, s'intégrera dans la plage de 10 kHz. C'est une quantité mesurable.

Vous pouvez le voir du troisième côté. Cette technologie n'est rien d'autre qu'un enregistrement d'hologramme, c'est-à-dire motif d'interférence qui se produit lorsque les champs de référence et de signal sont mélangés. Il contient les informations d'amplitude et de phase suffisantes pour restaurer l'image complète de l'objet.

Ainsi, en éclairant le satellite avec un laser, en enregistrant le signal réfléchi et en le mélangeant avec le faisceau de référence du même laser, nous obtenons un photocourant sur le photodétecteur, dont la dépendance temporelle reflète la structure du champ lumineux le long de "l'ouverture unidimensionnelle", dont la longueur, comme cela a déjà été dit, peut être faite assez gros.

Une ouverture en deux dimensions, bien sûr, est bien meilleure et plus informative. Disposons de manière uniforme plusieurs photodétecteurs sur le mouvement du satellite et écrivons ainsi le champ réfléchi sur la zone vt * L, où L est la distance entre les photodétecteurs extrêmes, qui est en principe illimitée. Par exemple, les mêmes 800 mètres. Ainsi, nous synthétisons l'ouverture du «télescope bidimensionnel» de 800 * 800 mètres. La résolution le long de la coordonnée transversale (L) dépendra du nombre de photodétecteurs et de la distance entre eux, de l'autre, de la coordonnée «temps» (vt) - de la bande passante d'émission laser et de la fréquence d'échantillonnage du signal du photodétecteur.

Nous avons donc un champ lumineux enregistré sur une très grande surface et nous pouvons tout faire avec. Par exemple, pour obtenir une image bidimensionnelle de très petits objets à une très grande distance sans aucun télescope. Ou vous pouvez restaurer la structure tridimensionnelle d'un objet en recentrant numériquement à portée.

Bien entendu, la configuration tridimensionnelle réelle des points réfléchissants sur l'objet ne coïncide pas toujours avec leur distribution "Doppler" sur les vitesses radiales. La coïncidence sera si ces points sont dans le même plan. Mais dans le cas général, beaucoup d'informations utiles peuvent être extraites de "l'image Doppler".

3. Ce qui s'est passé avant.

La DARPA américaine a financé le programme SALTI il y a quelque temps, dont l'essence était la mise en œuvre d'une telle technologie. Il était censé localiser des objets au sol (chars, par exemple) avec une résolution ultra-élevée depuis un avion volant, des données encourageantes ont été obtenues. Cependant, ce programme a été fermé ou classé en 2007 et depuis lors, on n'en a plus entendu parler. Quelque chose a été fait en Russie aussi. Ici, il est possible de voir l'image obtenue à une longueur d'onde de 10,6 microns.

4. Difficultés de mise en œuvre technique à une longueur d'onde de 1,5 microns.

Après mûre réflexion, j'ai décidé de ne rien écrire ici. Trop de problèmes.

5. Quelques résultats primaires.

Jusqu'à présent, il a été difficile «d'examiner» à une distance de 300 mètres les détails d'un objet métallique plat réfléchissant diffusement de 6 x 3 mm. Il s'agissait d'un morceau de carte de circuit imprimé, voici la photo:

l'objet a tourné autour d'un axe perpendiculaire à la ligne de visée, l'enregistrement du signal réfléchi s'est produit à peu près au moment de la réflexion maximale (éblouissement). Le spot laser éclairant l'objet mesurait environ 2 cm, seuls 4 photodétecteurs étaient utilisés, espacés de 0,5 mètre. La taille de l'ouverture synthétisée est estimée à 0,5 m par 10 m.
En fait, juste au cas où, les signaux enregistrés eux-mêmes (à gauche) et leurs spectres (à droite) en unités relatives: à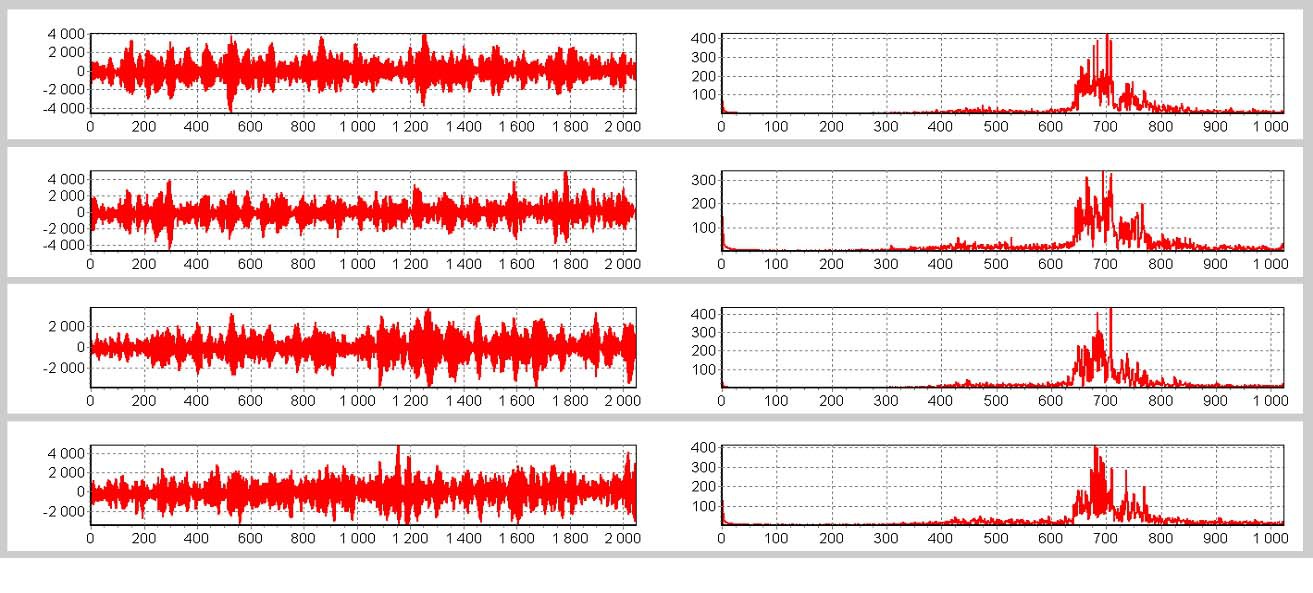

partir de la photo précédente de l'objet, photoshop n'a mis en évidence que les zones éclairées et réfléchissantes qui nous intéressent, qui sont nécessaires voir:

Image reconstruite par une transformée de Fourier bidimensionnelle de 4 signaux et mise à l'échelle pour comparaison:

cette image se compose en fait de seulement 4 lignes (et environ 300 colonnes), la résolution verticale de l'image, respectivement, est d'environ 0,5 mm, mais le coin sombre et les deux sont ronds les trous semblent être visibles. La résolution horizontale est de 0,2 mm, telle est la largeur des pistes conductrices sur la carte, les cinq pièces sont visibles. (Un télescope ordinaire doit avoir deux mètres de diamètre pour les voir dans le proche infrarouge).

En vérité, la résolution obtenue est encore loin de la limite théorique, il serait donc intéressant de penser à cette technologie. Le diable, comme vous le savez, est dans les détails, mais il y a beaucoup de détails.

Merci pour l'attention.

Source: https://habr.com/ru/post/fr383969/