Certains capteurs d'accélération nécessitent un étalonnage du zéro supplémentaire après montage sur la carte. Lorsque j'ai vu plusieurs sources avec l'étalonnage des capteurs d'accélération, où la composante G a été prise en compte simplement en soustrayant la valeur = 9,8 m / s2 de l'axe Z, l'idée est venue d'écrire cette note.
Structure de publication
- Problème
- Énoncé du problème et méthode de solution
- Comment obtenir les points?
- Comment calculer le centre de la balle?
- Comment accélérer la recherche du centre du ballon?
- Sinon, comment accélérer la recherche du centre du ballon?
- À propos des erreurs de mesure
- Total
Problème
Quel est le problème - les capteurs MEMS après l'installation dans la carte subissent des déformations mineures qui affectent:- position zéro;
- mise à l'échelle des valeurs mesurées;
- la perpendicularité des axes entre eux.
Et si la mise à l'échelle et la perpendicularité sont violées de manière moins visible, alors la position du zéro s'emmêle de manière tangible. Par exemple, si vous convertissez la valeur typique du décalage d'origine pour l'accéléromètre du capteur MPU9250 en m / s 2 , cela est obtenu dans la région de 0,2 m / s 2 . Autrement dit, le capteur est stationnaire, mais il montre une accélération, et après 5 secondes, nous obtenons une vitesse de 1 m / s. D'une part, toutes les données du capteur passent toujours par une sorte de filtre (par exemple, tel ). Mais d'un autre côté, pourquoi le filtre devrait-il constamment compenser ce biais? Après tout, le capteur montrera le mouvement là où il n'est pas. Cela réduit la précision du résultat. Dans l'ensemble, vous devez trouver la valeur de décalage une fois, puis soustraire cette valeur de ses lectures pendant le fonctionnement du capteur.La solution la plus simple pour trouver la valeur du décalage d'origine, qui vient immédiatement à l'esprit, est de créer les conditions dans lesquelles le capteur doit afficher avec précision zéro. La valeur enregistrée sur le capteur est la valeur du décalage d'origine! Donc? Mais aucune gravité n'agit constamment sur l'accéléromètre. Pour l'éviter, l'apesanteur sera nécessaire (le lancer ne fonctionnera pas). Le champ magnétique terrestre agit sur la boussole et sa rotation sur le gyroscope. Donc, si vous n'avez pas de vaisseau personnel, vous devrez trouver quelque chose.La deuxième solution qui vient immédiatement à l'esprit est de placer le capteur (ou plutôt son axe) dans une position dans laquelle nous saurons exactement ce que le capteur doit montrer. La différence entre ce que le capteur montre et ce qu'il devrait montrer - et il y aura un décalage nul! Donc? Par exemple, nous savons que si l'accéléromètre est placé au niveau de l'horizon, alors en théorie, le vecteur d'accélération gravitationnelle sera dirigé exactement le long de l'axe Z du capteur. La magnitude du vecteur d'accélération que nous connaissons.Cependant, il y a un problème. Elle consiste dans le fait qu'on ne peut pas régler précisément l'axe du capteur au niveau de l'horizon. Le fait est que la surface sur laquelle nous nous appuierons n'est pas parallèle à la carte de circuit imprimé. Cela, à son tour, n'est pas parallèle au site sur lequel le capteur est situé. Le capteur lui-même ne se tient pas exactement sur son emplacement et les axes à l'intérieur du capteur ne sont pas parallèles au corps du capteur. L'erreur dans le réglage de l'axe par rapport à l'horizon de 1 degré donne une projection comparable en taille à la valeur du décalage zéro lui-même, que nous voulons trouver. Dans le cas d'un magnétomètre, nous ne savons pas non plus où est dirigé le vecteur de champ magnétique. En théorie, au nord. Mais en pratique, le champ magnétique terrestre lui-même est hétérogène en intensité et en direction. De plus, les objets métalliques à proximité effectuent leurs ajustements.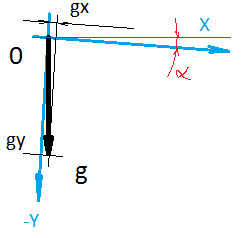
Énoncé du problème et méthode de solution
La tâche est la suivante: nous devons déterminer le vecteur de déplacement nul à l'aide du capteur, qui enregistrera toujours le vecteur de déplacement + vecteur d'impact externe constant (accélération gravitationnelle, rotation de la Terre, champ magnétique terrestre), dont nous ignorons l'amplitude et la direction (dans le cas de l'accéléromètre) nous connaissons la valeur, mais encore une fois l'échelle du capteur peut ne pas être égale à 1).La façon de résoudre. Cet article propose de déterminer le vecteur de déplacement comme suit. Nous prenons et tournons le capteur dans tous les sens et enregistrons les lectures du capteur. Après N mesures, les valeurs prises par le capteur et situées sur le graphique seront une boule, dont le rayon est la magnitude de l'impact externe, et le centre est le décalage d'origine exact souhaité.Comment obtenir les points?
Pour faciliter la procédure de mesure elle-même, vous pouvez écrire un programme simple. Il devrait enregistrer les capteurs lorsque l'appareil est à l'arrêt. Il suffit de tourner l'appareil dans la position souhaitée. Afin de déterminer un état stationnaire, un accéléromètre non calibré convient également - il suffit de prendre la différence entre la valeur actuelle et la précédente. Et s'il y a plus de bruit, alors on fixe le mouvement. Mon seuil est obtenu aux alentours de 0,07G. Si vous tenez avec vos mains, plus que cette valeur se révélera. J'ai utilisé du ruban adhésif pour fixer la position. Si cela ne fonctionne toujours pas, vérifiez s'il y a un réfrigérateur, un ventilateur ou quelque chose de similaire à proximité.Comment cela peut-il être en code
static TSumSensorsData g_sens_data[2];
static int32_t g_sens_data_sum_cnt[2];
static uint8_t g_sens_data_num;
IS_INTERRUPT void on_dma_raw_ready_calibrate_step1()
{
SensorRawBuffer *raw = sensor_get_raw_buffer();
g_sens_data[g_sens_data_num].acc_x += swap_i16(raw->accell_x_unswap);
g_sens_data[g_sens_data_num].acc_y += swap_i16(raw->accell_y_unswap);
g_sens_data[g_sens_data_num].acc_z += swap_i16(raw->accell_z_unswap);
g_sens_data[g_sens_data_num].gyro_x += swap_i16(raw->gyro_x_unswap);
g_sens_data[g_sens_data_num].gyro_y += swap_i16(raw->gyro_y_unswap);
g_sens_data[g_sens_data_num].gyro_z += swap_i16(raw->gyro_z_unswap);
g_sens_data[g_sens_data_num].mag_x += raw->mag_x_raw * g_mag_calibrate.kx;
g_sens_data[g_sens_data_num].mag_y += raw->mag_y_raw * g_mag_calibrate.ky;
g_sens_data[g_sens_data_num].mag_z += raw->mag_z_raw * g_mag_calibrate.kz;
g_sens_data_sum_cnt[g_sens_data_num]++;
}
void sensors_calibrate_program(FlashROM *flash_ptr)
{
double calibrate_result_error[3];
TVector16 calibrate_result[3];
int32_t radius[ACCEL_NO_MOTION_DETECT_COUNT];
uint8_t raw_is_deleted[ACCEL_NO_MOTION_DETECT_COUNT];
TVector16 raw[3][ACCEL_NO_MOTION_DETECT_COUNT];
. . .
g_sens_data_sum_cnt[0] = 0;
g_sens_data_num = 0;
int16_t prev_avg_x = 0;
int16_t prev_avg_y = 0;
int16_t prev_avg_z = 0;
int8_t low_motion_cnt = 0;
while(low_motion_cnt < ACCEL_NO_MOTION_DETECT_COUNT)
{
if (g_sens_data_sum_cnt[g_sens_data_num] >= ACCEL_NO_MOTION_DETECT_SAMPLES)
{
uint8_t new_data_num = (g_sens_data_num + 1) & 1;
g_sens_data[new_data_num].acc_x = 0;
g_sens_data[new_data_num].acc_y = 0;
g_sens_data[new_data_num].acc_z = 0;
g_sens_data[new_data_num].gyro_x = 0;
g_sens_data[new_data_num].gyro_y = 0;
g_sens_data[new_data_num].gyro_z = 0;
g_sens_data[new_data_num].mag_x = 0;
g_sens_data[new_data_num].mag_y = 0;
g_sens_data[new_data_num].mag_z = 0;
g_sens_data_sum_cnt[new_data_num] = 0;
uint8_t old_data_num = g_sens_data_num;
g_sens_data_num = new_data_num;
int16_t avg_x = g_sens_data[old_data_num].acc_x / g_sens_data_sum_cnt[old_data_num];
int16_t avg_y = g_sens_data[old_data_num].acc_y / g_sens_data_sum_cnt[old_data_num];
int16_t avg_z = g_sens_data[old_data_num].acc_z / g_sens_data_sum_cnt[old_data_num];
int16_t dx = avg_x - prev_avg_x;
int16_t dy = avg_y - prev_avg_y;
int16_t dz = avg_z - prev_avg_z;
prev_avg_x = avg_x;
prev_avg_y = avg_y;
prev_avg_z = avg_z;
if ((abs_i16(dx) <= ACCEL_NO_MOTION_DETECT_AVG_VALUE)&&(abs_i16(dy) <= ACCEL_NO_MOTION_DETECT_AVG_VALUE)&&(abs_i16(dz) <= ACCEL_NO_MOTION_DETECT_AVG_VALUE))
{
raw[RAW_ACC][low_motion_cnt].x = avg_x;
raw[RAW_ACC][low_motion_cnt].y = avg_y;
raw[RAW_ACC][low_motion_cnt].z = avg_z;
raw[RAW_GYRO][low_motion_cnt].x = g_sens_data[old_data_num].gyro_x / g_sens_data_sum_cnt[old_data_num];
raw[RAW_GYRO][low_motion_cnt].y = g_sens_data[old_data_num].gyro_y / g_sens_data_sum_cnt[old_data_num];
raw[RAW_GYRO][low_motion_cnt].z = g_sens_data[old_data_num].gyro_z / g_sens_data_sum_cnt[old_data_num];
raw[RAW_MAG][low_motion_cnt].x = g_sens_data[old_data_num].mag_x / g_sens_data_sum_cnt[old_data_num];
raw[RAW_MAG][low_motion_cnt].y = g_sens_data[old_data_num].mag_y / g_sens_data_sum_cnt[old_data_num];
raw[RAW_MAG][low_motion_cnt].z = g_sens_data[old_data_num].mag_z / g_sens_data_sum_cnt[old_data_num];
low_motion_cnt++;
beep();
delay_ms(2000);
}
}
}
. . .
}
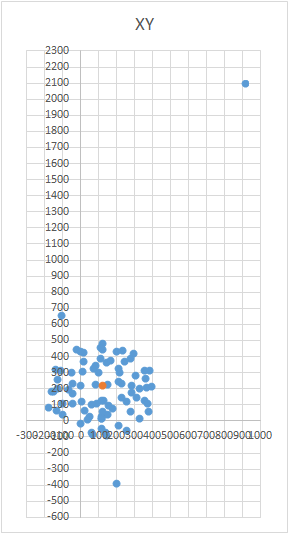
Pour obtenir la balle sur le graphique, vous devez tordre l'appareil avec le capteur selon un certain schéma. À ces fins, le globe est bien adapté, car il a un balisage. Vous pourriez penser que vous devez sculpter partout dans le monde. Mais ce n'est pas le cas.Exemple de résultat incorrect Il est nécessaire de sculpter le capteur non pas sur toute la surface du globe, mais sur un méridien. Supposons que nous prenions sept points sur le méridien (le premier et le dernier aux pôles nord et sud). À chaque point du méridien, nous attachons votre appareil au globe et nous tournons toujours l'appareil autour de son axe avec un certain pas, par exemple de 30 à 35 degrés. Il s'avère que si vous tournez 12 fois autour de son axe, alors en 7 points au total 84 mesures sont obtenues.
La beauté de la méthode est que tout peut être fait «sur le genou». La précision de positionnement ne joue pas un rôle particulier, il suffit de tordre selon le schéma pour que le vecteur d'influence externe sur le graphique dessine une balle. Le bon ressemble à quelque chose comme ceci - voir la figure (le centre est marqué d'une marque).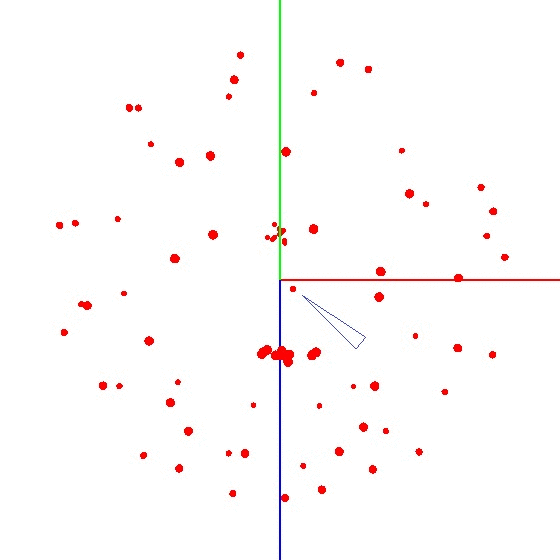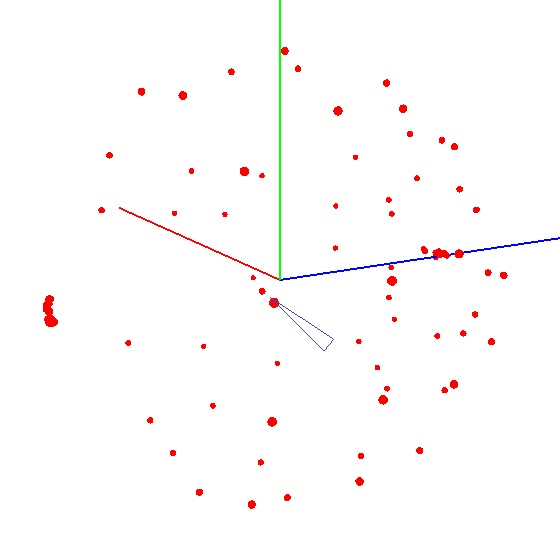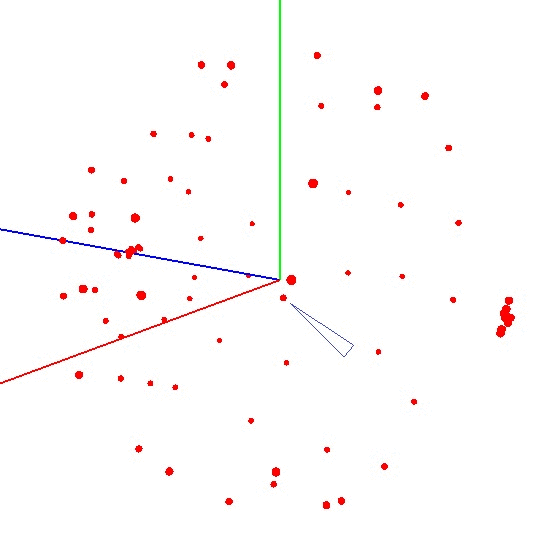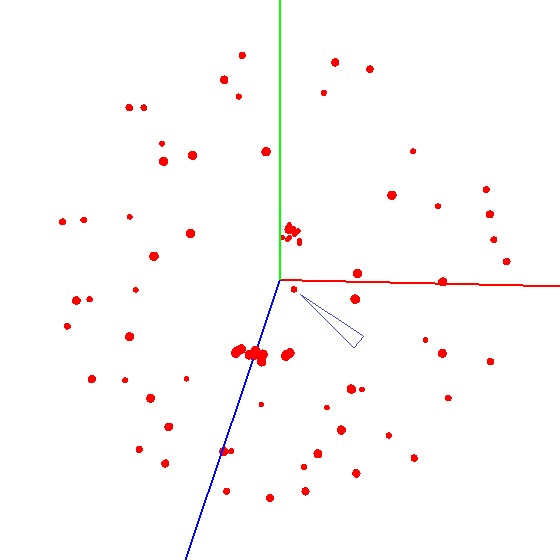
Comment calculer le centre de la balle?
C'est une tâche intéressante et elle a plusieurs solutions. Il peut sembler que pour rechercher le centre, il suffit de prendre la moyenne arithmétique des coordonnées des points obtenus. Cependant, ce n'est pas le cas - les points peuvent être situés de manière inégale sur le ballon (voir. Fig.).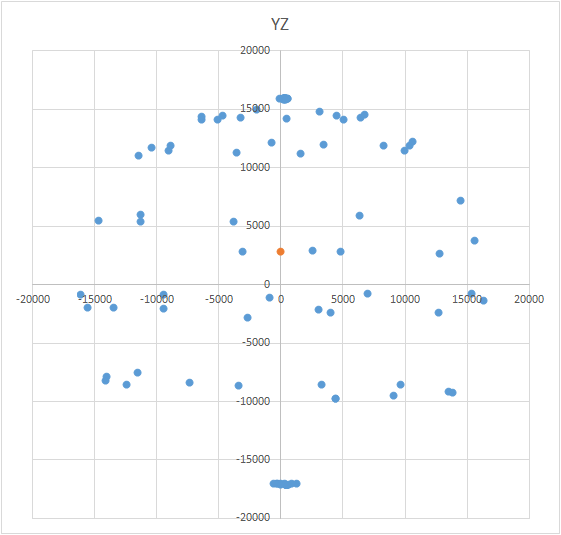
L'équation de la balle ressemble à ceci: (X - A) 2 + (Y - B) 2 + (Z - C) 2 = R 2 , où X, Y, Z sont les coordonnées du point se trouvant sur la balle. A, B, C sont les coordonnées du centre sur les axes x, y et z, respectivement. R est le rayon de la balle. Vous pouvez construire un système d'équations et essayer de résoudre ce système plus simplement en utilisant une méthode. Ou vous pouvez simplement casser pour trouver le centre (c'est comme une méthode d'approximations successives). La signification de la méthode est simple: la valeur d'erreur (X - A) 2 + (Y - B) 2+ (Z - C) 2 - R 2 devrait tendre vers zéro. Cela signifie que la somme de ces quantités pour tous les points de la sphère devrait également tendre vers zéro. Sachant cela, nous pouvons choisir les valeurs A, B et C pour lesquelles l'erreur pour tous les points sera minimale. La zone de recherche est limitée par la taille de la balle (cube conditionnel). Autrement dit, nous devons mettre séquentiellement le centre de la balle à tous les points du cube et calculer l'erreur. Là où il y a une erreur minimale - il y a le centre.
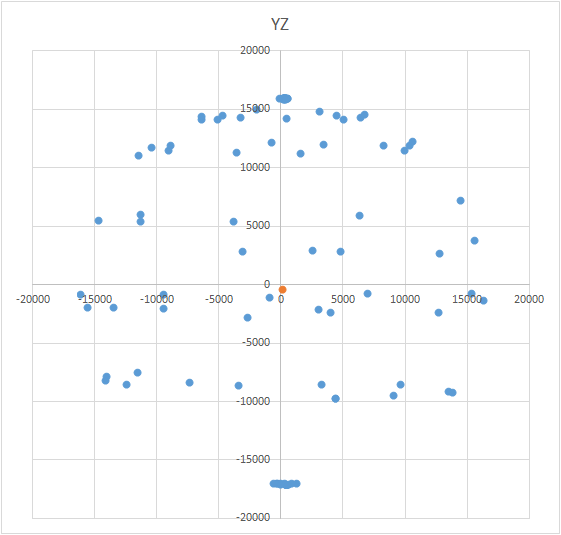En tant que R, nous devons prendre la valeur théorique du vecteur d'influence externe - pour l'accéléromètre, c'est l'accélération de la gravité, pour la boussole - c'est la magnitude moyenne du champ magnétique terrestre, pour le gyroscope - la vitesse de rotation de la Terre. Bien sûr, dans la formule, il devrait y avoir des valeurs d'une dimension (unités conventionnelles du capteur ou m / s 2, degrés / s, etc.). Il est plus pratique de convertir en unités arbitraires du capteur correspondant.Comment calculer une certaine valeur dans les unités standard du capteur?= * / ( — )
: 16- ±2g ?:
9,8 /2 * 65536 / (2g + 2g) = 9,8 /2 * 65536 / (2 * 9,8 /2 + 2 * 9,8 /2) = 16384 . . .
Soit dit en passant, si vous connaissez exactement le rayon de la balle, vous ne pouvez calculer le centre que par son «coin». Autrement dit, à des points qui sont situés uniquement sur un morceau de la surface de la balle. Mais ce n'est pas notre cas.Comment accélérer la recherche du centre du ballon?
Il est nécessaire de rechercher le centre non pas dans le cube entier (les dimensions de la balle), mais le long de la ligne, dont le début est arbitraire, chaque point suivant est plus proche du centre réel et la fin est au centre. Supposons que nous partions du point (0; 0; 0) ... Nous nous déplaçons toujours avec un pas constant. Par conséquent, si nous imaginons un ensemble de cubes 3x3x3, où chaque face est égale à la taille du pas et imaginons également que la position actuelle est le cube du milieu, nous avons 9 + 8 + 9 options où placer le point suivant. Il suffit d'être à chaque point pour calculer dans lequel des 26 points voisins l'erreur sera moindre. S'il s'avère que l'erreur est moindre au point actuel, et non à l'un des voisins, cela signifie qu'elle est au centre et que la recherche est terminée.
Comment cela peut-il être en codePublic Function get_err(A As Double, B As Double, C As Double, R As Double) As Double
Dim x, y, z As Double
Dim sigma As Double
Dim row_n As Long
get_err = 0
For row_n = 1 To 15
x = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 1).Value
y = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 2).Value
z = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 3).Value
get_err = get_err + abs( (A - x) ^ 2 + (B - y) ^ 2 + (C - z) ^ 2 - R ^ 2 )
Next
End Function
. . .
A = 0
B = 0
C = 0
Do While True
min_sigma = 0
For ai = -1 To 1
For bi = -1 To 1
For ci = -1 To 1
sigma = get_err(A + ai, B + bi, C + ci, 16384)
If sigma < min_sigma Or min_sigma = 0 Then
ai_min = ai
bi_min = bi
ci_min = ci
min_sigma = sigma
End If
Next
Next
Next
If ai_min = 0 And bi_min = 0 And ci_min = 0 Then
Exit Do
End If
A = A + ai_min
B = B + bi_min
C = C + ci_min
Loop
. . .
Sinon, comment accélérer la recherche du centre du ballon?
Besoin de rechercher avec un pas variable. Nous recherchons d'abord le centre par grandes étapes. Nous avons trouvé le centre, nous réduisons le pas et nous commençons à chercher plus loin. Et ainsi de suite, jusqu'à ce que vous obteniez le résultat de la précision nécessaire.Comment cela peut-il être en codePublic Function get_err(A As Double, B As Double, C As Double, R As Double) As Double
Dim x, y, z As Double
Dim sigma As Double
Dim row_n As Long
get_err = 0
For row_n = 1 To 15
x = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 1).Value
y = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 2).Value
z = Application.ActiveWorkbook.ActiveSheet.Cells(row_n, 3).Value
get_err = get_err + abs( (A - x) ^ 2 + (B - y) ^ 2 + (C - z) ^ 2 - R ^ 2 )
Next
End Function
. . .
A = 0
B = 0
C = 0
step = 1000
Do While True
min_sigma = 0
For ai = -1 To 1
For bi = -1 To 1
For ci = -1 To 1
sigma = get_err(A + ai * step, B + bi * step, C + ci * step, 16384)
If sigma < min_sigma Or min_sigma = 0 Then
ai_min = ai
bi_min = bi
ci_min = ci
min_sigma = sigma
End If
Next
Next
Next
If ai_min = 0 And bi_min = 0 And ci_min = 0 Then
step = step / 10
If step < 0.01 Then
Exit Do
End If
Else
A = A + ai_min * step
B = B + bi_min * step
C = C + ci_min * step
End If
Loop
. . .
À propos des erreurs de mesure
Pendant les mesures, il peut y avoir des situations où, pour une raison quelconque, le résultat de la mesure peut être beaucoup plus éloigné de la surface de la balle. Ou cela pourrait être beaucoup de points. Ou, en général, le résultat des mesures peut ne pas être une balle, mais un «œuf» ou un «dirigeable». Dans ce cas, bien sûr, vous devez répéter toutes les mesures, en identifiant les causes possibles des erreurs. Par exemple, pour un magnétomètre, il peut s'agir d'un boulon ou d'un clou dans une table et vous prenez des mesures directement au-dessus. Et plus vous abaissez le capteur le long du méridien, plus le métal sera fort affectera le résultat. Par conséquent, il est nécessaire de déterminer le seuil de la valeur d'erreur admissible. Afin de ne pas refaire les mesures en raison de plusieurs points clairement erronés, vous pouvez appliquer un filtre. Le principe du filtre est très simple - après avoir calculé le centre pour la première fois, triez les points par niveau d'erreur dans chacun d'eux.Certains des points avec l'erreur la plus importante peuvent simplement être jetés (par exemple, 10%). Ensuite, vous devez répéter la recherche du centre.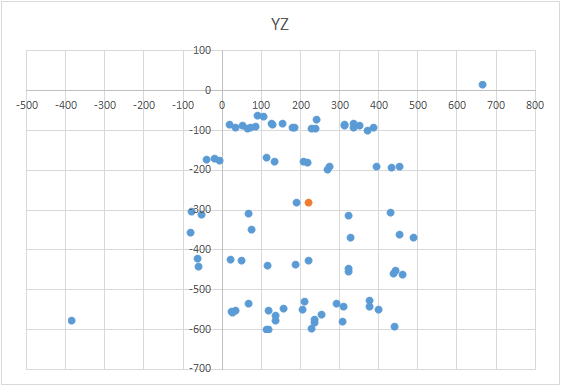
Total
La méthode a une assez bonne précision. La méthode vous permet de faire avec des moyens improvisés simples (balle, banque, etc.). Cela fonctionne assez vite. Code simple. De nombreux capteurs ont des registres spéciaux où vous pouvez écrire la valeur trouvée, et le capteur la soustraira à la volée. Ces registres ont généralement le préfixe «TRIM», comme dans le MPU9260, ou «OFFSET», comme dans le LSM303. Mais le bien connu LIS302DL ne dispose pas de tels registres.N'oubliez pas de mettre un signe plus si cela vous a plu. Écrivez dans les commentaires vos méthodes d'étalonnage des capteurs.