Les scientifiques ont inventé de nouvelles façons de couper la pizza

Les mathématiciens de l'Université de Liverpool, dans leurs nouveaux travaux, ont publié plusieurs façons auparavant inconnues de partitionner le disque en parties égales. Ce travail appartient à la section de la géométrie, l'étude de la soi-disant parquets - carrelage de l'avion avec des polygones sans lacunes et chevauchements. Les scientifiques ont été inspirés pour trouver des façons de couper la pizza, une procédure familière à la plupart d'entre nous.

Lorsque vous inclinez l'avion avec des figures géométriques (tuiles), vous pouvez définir et résoudre différents problèmes. L'une des tâches les plus intéressantes est l'utilisation de carreaux monoédriques. Dans ce cas, toutes les tuiles ont la même forme ou, plus précisément, sont congruentes. Cela signifie que deux tuiles peuvent être combinées à l'aide de mouvements, de virages ou de réflexion de miroir.

L'ensemble des formes de tuiles utilisées pour remplacer l'avion est appelé proto-tuiles. Il est intéressant de noter qu'aucune méthode mathématique ne vous permet de dire à l'avance s'il est possible de remplacer un avion à l'aide de protoplates données. Par exemple, il est connu que sur les 24 heptamonds suivants (figures composées de sept triangles équilatéraux), un seul ne convient pas pour le carrelage monohédrique d'un avion. Mais lequel?



Dans ce cas - en forme de V. Mais la preuve de cela est une tâche plutôt non triviale.

Cependant, les mathématiciens de Liverpool, au lieu d'un avion entier, se sont limités à un disque et ont commencé à rechercher des proto-tuiles monoédriques adaptées à la division du disque. Une version de ces protoplates est connue de tous. Avec la méthode standard de coupe de pizza, elle est divisée en segments égaux de forme triangulaire, dont les sommets convergent au centre du disque. Les scientifiques ont décidé de répondre à la question - existe-t-il de telles divisions du disque en chiffres égaux dans lesquels tous ces chiffres ne touchent pas le centre du disque?

Autrement dit, est-il possible de couper la pizza en parts égales afin de plaire à la fois à ceux qui aiment plus de garnitures et à ceux qui aiment plus de croûtes? Il s'est avéré que c'était possible. De plus, une version de cette coupe est connue depuis longtemps et se trouve sur le logo de la communauté de l'Université de Pennsylvanie , qui organise des séminaires de mathématiques pour les étudiants: les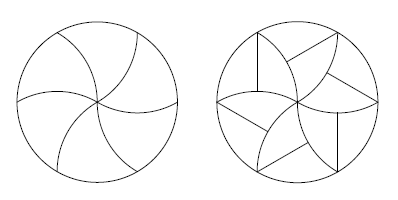



tranches figurées peuvent être divisées en deux et toutes les parties seront congruentes, avec seulement la moitié d'entre elles touchant le centre.

Les mathématiciens ont développé cette idée et ont proposé leurs propres méthodes de division d'un disque en un nombre presque infini de parties égales.







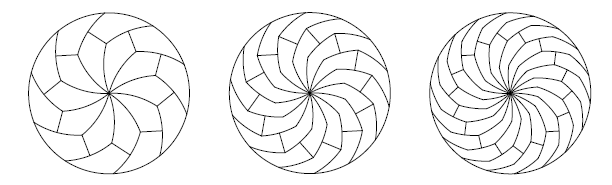Comme c'est souvent le cas en mathématiques, les possibilités d'appliquer les idées de travail dans la pratique ne sont pas tout à fait évidentes - sauf si, en utilisant une pizza de coupe de pizza non standard comme un avantage concurrentiel. Mais d'un autre côté, il est également impossible de prévoir comment une découverte mathématique sera utile à l'avenir.

Source: https://habr.com/ru/post/fr389011/