Qu'arrivera-t-il à l'œil si vous regardez à travers le télescope au coucher du soleil?

Je répondrai immédiatement à la question posée dans le titre - il ne se passera rien de mal. J'ai fait ça, et j'ai regardé tout de suite avec des jumelles avec deux yeux. Ici, ils ne m'ont pas cru, j'écris cet article comme preuve (je l'écris moi-même, pas le secrétaire dicté).

Important: avant le coucher du soleil, lorsque le soleil n'a pas encore touché l'horizon, vous n'avez pas besoin de regarder, de brûler le trou indiqué dans l'article. Qu'arrivera-t-il à l'œil si vous regardez à travers le télescope vers le soleil? Sous l'horizon se réfère à l'horizon «réel» et non au toit d'une maison voisine.


Lorsque le soleil est près de l'horizon, ses rayons parcourent un chemin beaucoup plus large à travers l'atmosphère.



Pour savoir combien cela représente et combien de fois la luminosité diminue, nous empruntons les calculs de l'article Absorption atmosphérique ou comment évaluer la pollution de l'air .

La masse atmosphérique (eng: airmass ) est une quantité sans dimension exprimant la longueur de trajet d'un rayon de lumière dans l'atmosphère aux hauteurs d'une «atmosphère homogène». Comme nous l'a montré Kirill Grishin AKA Lord_Katler_Bekket , vous pouvez le calculer en utilisant la formule suivante: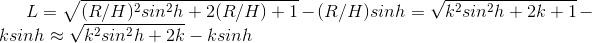



k = R / H est le rapport du rayon de la Terre et de la hauteur d'une atmosphère homogène (k = 800). L'angle h est la hauteur de l'étoile, les distances R , H et Lcomme le montre ce diagramme:



comme au coucher du soleil h = 0 , la formule dégénère en.



Ainsi, nous obtenons L = 40 , c'est-à-dire qu'à l'horizon le rayon solaire dépasse quarante fois plus d'air qu'au zénith. Est-ce beaucoup ou peu? Allons plus loin. La loi de Bouger - Lambert - Bière en magnitudes stellaires a une forme assez simple: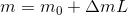



Ici:
m est la magnitude stellaire observée
m ₀ est la luminosité de l'étoile en dehors de l'atmosphère
Δm est l'absorption atmosphérique au zénith en quantités stellaires
L est la masse d'air

Nous prenons Δm pour 0,35, ce qui est encore moins que l'expérimental estimations de Cyril. Si vous prenezm _{0 du} Soleil pour −26,7, puis m du Soleil au coucher du soleil sera de -12,7, ce qui coïncide pratiquement avec la magnitude de la pleine Lune et correspond à une baisse de luminosité de 400 000 fois ! Si vous avez déjà observé une pleine lune sans filtre «lunaire» à travers un télescope, alors vous savez que ce n'est pas très agréable à l'œil, mais supportable. Si vous êtes gêné que la luminosité de surface ne soit pas prise en compte dans les calculs, je peux dire qu'elle peut être «crochue», car le diamètre angulaire des disques solaires et lunaires est sensiblement le même.

Donc, dans des conditions urbaines poussiéreuses, vous pouvez toujours regarder le coucher du soleil avec votre œil armé et ne pas souffrir. N'essayez pas de le faire dans les montagnes, où l'air est propre et Δm sera d'environ 0,2, et Lva diminuer un peu.

Vous pouvez vérifier les calculs dans le Stellarium : il



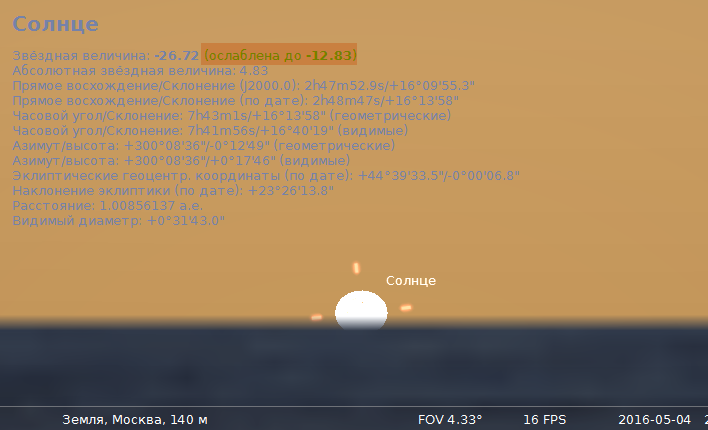vous suffit de définir la valeur correspondante Δm dans les paramètres (dans la localisation russe, cela se traduit par «coefficient d'extinction»).



Le lecteur peut se demander pourquoi au coucher du soleil, il est encore beaucoup plus léger que la nuit à la pleine lune. Le fait est qu'au coucher du soleil, le paysage environnant est éclairé non seulement par la lumière directe diminuée du Soleil, mais aussi par la lumière diffusée dans la haute atmosphère.

PS: J'ai pris la photo au début de l'article sans aucun filtre et je n'ai pas ruiné l'appareil photo. L'image montre un groupe de taches AR2396 , rappelant la forme d'une empreinte.

Source: https://habr.com/ru/post/fr393597/