Demandez à Ethan n ° 78: pourquoi E = mc2?
L'équation la plus célèbre d'Einstein est calculée plus magnifiquement que ce à quoi on pourrait s'attendre.
Il résulte de la théorie spéciale de la relativité que la masse et l'énergie sont des manifestations différentes de la même chose - un concept inconnu de l'esprit moyen.
- Albert Einstein
Certains concepts scientifiques changent tellement le monde et sont si profonds que presque tout le monde les connaît, même s'ils ne les comprennent pas pleinement. Pourquoi ne pas y travailler ensemble? Chaque semaine, vous envoyez vos questions et suggestions, et cette semaine, j'ai choisi une question de Mark Liyuv, qui demande:Einstein a dérivé l'équation E = mc 2 . Mais les unités d'énergie, de masse, de temps, de longueur étaient déjà connues avant Einstein. Alors, comment ça se passe si bien? Pourquoi n'y a-t-il pas de constante de durée ou de temps? Pourquoi n'est-ce pas E = amc 2 , où a est une constante?Si notre Univers n'avait pas été arrangé tel qu'il est maintenant, alors tout aurait pu être différent. Voyons ce que je veux dire.
D'une part, nous avons des objets avec des masses: des galaxies, étoiles et planètes aux plus petites molécules, atomes et particules fondamentales. Bien qu'ils soient minuscules, chacun des composants de ce que nous connaissons sous le nom de matière a une propriété fondamentale de masse, ce qui signifie que même si nous excluons son mouvement, même si nous le ralentissons jusqu'à l'arrêt complet, cela affectera toujours tous les autres objets de l'univers.
Plus précisément, il exerce une attraction gravitationnelle sur tout le reste de l'Univers, quelle que soit la distance de l'objet distant. Il attire tout pour lui, est attiré par tout le reste et possède également l'énergie inhérente à son existence même.La dernière affirmation est contre-intuitive, car l'énergie, au moins en physique, est considérée comme la possibilité de faire quelque chose - la capacité de travailler. Et que pouvez-vous faire si vous restez simplement assis?Avant de répondre, regardons l'autre côté de la médaille - des choses sans masse.
D'un autre côté, il y a des choses qui n'ont pas de masse - par exemple, la lumière. Ces particules ont une certaine énergie, ce qui est facile à comprendre en observant leur interaction avec d'autres choses - lorsqu'elle est absorbée, la lumière leur transfère son énergie. La lumière avec une énergie suffisante peut chauffer la matière, ajouter de l'énergie cinétique (et de la vitesse), cogner des électrons à des niveaux d'énergie plus élevés, ou même ioniser, selon l'énergie.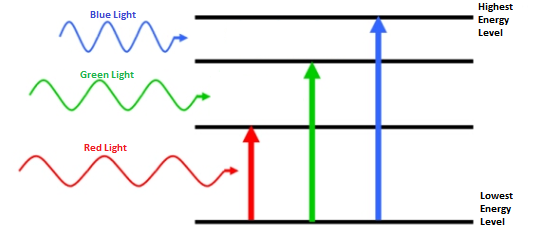
De plus, la quantité d'énergie contenue dans une particule sans masse n'est déterminée que par sa fréquence et sa longueur d'onde, dont le produit est toujours égal à la vitesse de la particule: la vitesse de la lumière. Cela signifie que les ondes plus longues ont des fréquences plus basses et moins d'énergie, tandis que les ondes courtes ont des fréquences et une énergie plus élevée. Une particule massive peut être ralentie, et les tentatives de prendre l'énergie d'une masse sans masse ne conduiront qu'à une extension de son onde, et non à un changement de vitesse.
Gardant cela à l'esprit, pensons comment la masse-énergie peut être équivalente au travail? Oui, vous pouvez prendre une particule de matière et une particule d'antimatière (électron et positron), les pousser ensemble et obtenir des particules sans masse (deux photons). Mais pourquoi les énergies de deux photons sont-elles égales aux masses d'un électron et d'un positron multipliées par le carré de la vitesse de la lumière? Pourquoi n'y a-t-il pas d'autre facteur, pourquoi l'équation équivaut-elle exactement à E et mc 2 ?
Ce qui est intéressant, selon SRT, l'équation doit simplement ressembler à E = mc 2 , sans aucun écart. Parlons des raisons de cela. Tout d'abord, imaginez que vous avez une boîte dans l'espace. Il est immobile, et il a des miroirs des deux côtés, et à l'intérieur se trouve un photon volant vers l'un des miroirs.
Initialement, la boîte ne bouge pas, mais comme les photons ont de l'énergie (et de l'élan), lorsque le photon entre en collision avec le miroir d'un côté de la boîte et rebondit, la boîte commencera à se déplacer dans la direction dans laquelle le photon s'est déplacé à l'origine. Lorsque le photon atteint l'autre côté, il rebondit sur le miroir de l'autre côté, remettant à zéro l'élan de la boîte. Et cela continuera de se refléter de cette manière, tandis que la boîte se déplacera à mi-chemin dans une direction et que l'autre moitié restera immobile.En moyenne, la boîte se déplacera et, donc, comme elle a de la masse, elle aura une certaine énergie cinétique, grâce à l'énergie du photon. Mais il est également important de se souvenir de l'impulsion, de l'élan de l'objet. La quantité de mouvement des photons est très simplement liée à leur énergie et à leur longueur d'onde: plus l'onde est courte et plus l'énergie est élevée, plus la quantité de mouvement est élevée.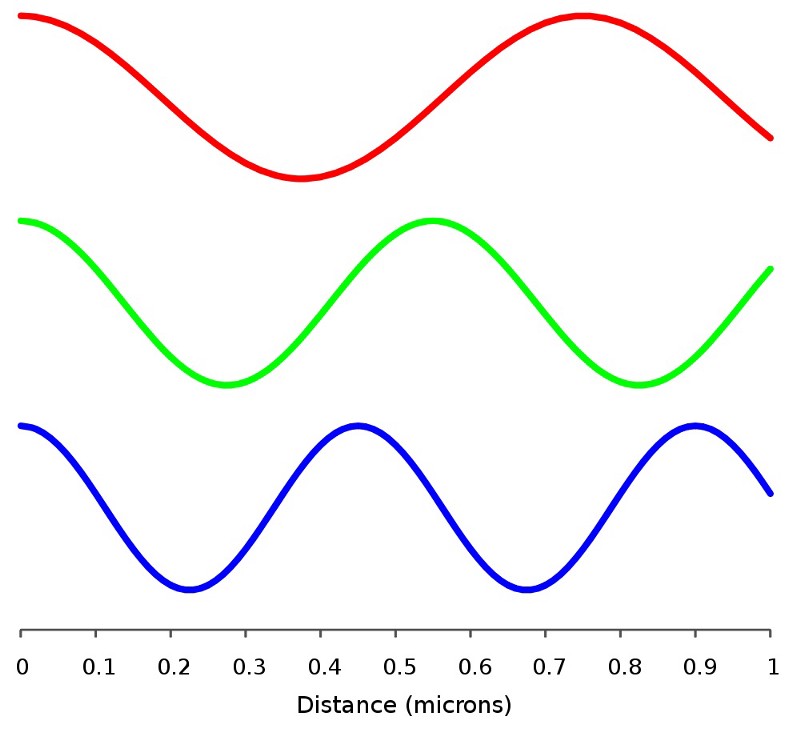
Réfléchissons à ce que cela signifie, et pour cela, nous allons mener une autre expérience. Imaginez ce qui se passe lorsque seul le photon lui-même se déplace initialement. Il aura une certaine quantité d'énergie et d'élan. Les deux propriétés doivent être préservées, donc au moment initial, l'énergie du photon est déterminée par sa longueur d'onde, et la boîte n'a que de l'énergie de repos - quelle qu'elle soit - et le photon a toute la dynamique du système, et la quantité de mouvement de la boîte est nulle.
Ensuite, le photon entre en collision avec la boîte et est temporairement absorbé. L'élan et l'énergie doivent être conservés - ce sont les lois fondamentales de la conservation de l'Univers. Si le photon est absorbé, il n'y a qu'une seule façon de maintenir l'élan - la boîte devrait se déplacer à une certaine vitesse dans la même direction dans laquelle le photon se déplaçait.Jusqu'à présent, tout va bien. Ce n'est que maintenant que nous pouvons nous demander quelle est l'énergie de la boîte. Il s'avère que si nous partons de notre formule habituelle pour l'énergie cinétique, K E = ½mv 2 , nous connaissons vraisemblablement la masse de la boîte et, sur la base du concept d'élan, sa vitesse. Mais si nous comparons l'énergie de la boîte avec l'énergie du photon qu'il possédait avant la collision, nous verrons que la boîte a une énergie insuffisante.Un problème? Non, c'est assez simple à résoudre. L'énergie du système boîte / photon est égale à la masse au repos de la boîte plus l'énergie cinétique de la boîte plus l'énergie du photon. Quand une boîte absorbe un photon, la plus grande partie de son énergie va à augmenter la masse de la boîte. Lorsque la boîte a absorbé un photon, sa masse change (augmente) par rapport à ce qu'elle était avant la collision.Lorsque la boîte émet à nouveau un photon dans l'autre sens, elle reçoit une impulsion et une vitesse encore plus grandes (qui sont compensées par l'impulsion négative du photon dans la direction opposée), encore plus d'énergie cinétique (et le photon a de l'énergie), mais perd une partie de la masse restante en retour. Si tout est calculé (il existe trois façons différentes de le faire, et il y a aussi une description), vous pouvez constater que la seule transformation de masse qui vous permet d'économiser de l'énergie et de l'élan est E = mc2 .
Si vous ajoutez une constante, l'équation cessera d'être équilibrée et vous perdrez ou gagnerez de l'énergie à chaque fois que vous émettez ou absorbez un photon. Ayant découvert l'antimatière dans les années 1930, nous avons directement vu la confirmation que l'énergie peut être convertie en masse et vice versa, et les résultats des transformations coïncidaient exactement avec E = mc 2 , mais c'est grâce à des expériences mentales que cette formule a pu être dérivée plusieurs décennies avant les observations. Ce n'est qu'en alignant le photon avec la masse effective équivalente à m = E / c 2 que nous pouvons garantir la conservation de l'énergie et de la quantité de mouvement. Et bien que nous disions E = mc 2 , Einstein a d'abord écrit la formule différemment, attribuant la masse équivalente en énergie aux particules sans masse.Donc, merci pour la merveilleuse question, Mark, et j'espère que cette expérience de pensée vous aidera à comprendre pourquoi nous avons besoin non seulement de l'équivalence de la masse et de l'énergie, mais aussi pourquoi il n'y a qu'une seule valeur possible pour la «constante» dans cette équation, ce qui aidera à préserver l'énergie et l'élan - et c'est ce dont notre Univers a besoin. La seule équation qui fonctionne est E = mc 2 . Envoyez-moi vos questions et suggestions pour les articles suivants.Source: https://habr.com/ru/post/fr396379/
All Articles