Vous voulez énigmer un joueur d'échecs débutant?Demandez-lui de mater avec un cheval et un éléphant.Vous voulez surprendre un programmeur novice?Demandez-lui de calculer le tapis avec un cheval et un éléphant.
Les problèmes d'échecs excitent l'imagination du programmeur,c'est pourquoi pour la démonstration pratique de la combinatoirej'ai choisi le problème d'échecs le plus difficile du cycle "échec et mat au roi solitaire".Fixation d'objectifs
Le but du projet est de créer une base de solutions, c'est-à-dire une liste des bons mouvements pour tous les emplacements possibles du roi blanc, de l'éléphant, du cheval et du roi noir sur l'échiquier.Dans cette publication, je vais vous expliquer comment j'ai résolu ce problème, quelles difficultés j'ai dû affronter, et aussi vous montrer ce qui s'est finalement produit. Technologies utilisées: C #, JavaScript, PHP, HTML, CSS.Étant un joueur d'échecs très médiocre, je n'ai jamais appris à mater rapidement avec un cheval et un éléphant. Par conséquent, j'ai décidé de compenser cette lacune par mes compétences en programmation, de trier toutes les positions possibles et de trouver le bon choix pour chacune.Avant d'écrire au moins une ligne de code, j'ai élaboré un plan «napoléonien» sur la façon dont je le ferais pendant plusieurs semaines. Je voulais vraiment commencer à résoudre ce problème depuis la fin, en triant toutes les combinaisons mates. Et puis, faites un pas en arrière jusqu'à ce que toutes les options possibles soient épuisées.Combien d'options existe-t-il?
Il y a 64 cellules sur un échiquier. Nous avons quatre chiffres.Le nombre de combinaisons possibles est 64 * 64 * 64 * 64 = 16 777 216.Vous ne pouvez laisser qu'un éléphant à poitrine blanche.Le nombre d'options sera divisé par deux: 64 * 32 * 64 * 64 = 8 388 608.Tant de postes seront dans notre base de données de solutions.En fait, il y a encore moins de combinaisons: deux pièces ne peuvent pas se tenir sur une case, les rois ne peuvent pas se tenir sur des cases adjacentes, le roi noir ne peut pas être sous le contrôle, et ainsi de suite. Pour l'avenir, je dirai que la base de données des solutions s'est avérée être 5 609 790 combinaisons, le tableau sera rempli de 67%.Cependant, pour simplifier l'algorithme et accélérer l'accès aux données de la base de données, j'ai décidé de ne pas «perdre de temps dessus» et de créer un tableau à quatre dimensions pour toutes les combinaisons.La structure suivante est définie pour stocker chaque combinaison: struct Combo
{
public Coord whiteKing;
public Coord whiteBishop;
public Coord whiteKnight;
public Coord blackKing;
}
À l'intérieur, une autre structure Coord est utilisée pour enregistrer les coordonnées de la figure, avec la possibilité de calculer l'indice de 0 à 63, ainsi qu'avec un opérateur de comparaison surchargé. public struct Coord
{
public byte x;
public byte y;
public int index
{
get { return x + y * 8; }
set { x = (byte) (value % 8);
y = (byte) (value / 8); }
}
public static bool operator == (Coord a, Coord b)
{
return a.x == b.x && a.y == b.y;
}
}
Cette structure s'est avérée très pratique pour passer comme argument à diverses fonctions auxiliaires, par exemple: bool isCheck (Combo combo);
bool isCheckmate (Combo combo);
bool isCheckByBishop (Combo combo);
Cependant, pour enregistrer le résultat de la base de décisions de cette structure ne suffit pas, nous avons encore besoin ...Boîte blanche
L'objectif de notre programme sera de créer une "boîte blanche", dans laquelle toutes les positions dans lesquelles le "mouvement est blanc", et pour lesquelles on sait quel mouvement prendre, et à travers combien de mouvements il sera garanti de mater, seront additionnées.Une partie intégrante de la «boîte blanche» est la structure suivante: struct WhitesMove
{
public Combo combo;
public byte moves;
public Coord moveFrom;
public Coord moveTo;
}
La façon la plus simple d'organiser une «boîte blanche» consiste à ouvrir une matrice à quatre dimensions. Chaque dimension de cette matrice correspond à la position possible de chaque figure: WhitesMove [ , , , ] box = new WhitesMove [64, 32, 64, 64];
la première dimension est la coordonnée du roi blanc.la deuxième dimension est la coordonnée de l'éléphant blanc / 2. latroisième dimension est la coordonnée du cheval blanc.la quatrième dimension est la coordonnée du roi noir.L'essentiel est de ne pas confondre leur commande :) Le tableau s'avérera être déchargé à 33%, mais très pratique pour le traitement. C'est dans ce tableau que 8 388 608 entrées seront stockées pour résoudre les combinaisons.Soit dit en passant, avant de commencer à écrire tous les algorithmes de recherche, j'ai créé un projet vide et initialisé cette matrice à quatre dimensions, afin de s'assurer qu'il y a suffisamment de mémoire et qu'il ne sera pas nécessaire d'inventer quelque chose de plus. Apparemment, l'expérience de participer aux olympiades informatiques du dernier millénaire, où la taille de la structure ne pouvait pas dépasser 64 kilo-octets, a affecté Turbo Pascal 7.0.Idée de l'algorithme
Décrivez brièvement l'idée principale de résoudre ce problème. Il est basé sur un premier algorithme de recherche, qui a dû être légèrement modifié, car deux personnes jouent aux échecs et des mouvements sont effectués à tour de rôle. Par conséquent, au lieu d'une ligne, nous avons besoin de deux - «noir» et «blanc». Queue<BlacksMove> blackQueue = new Queue<BlacksMove>();
Queue<WhitesMove> whiteQueue = new Queue<WhitesMove>();
Avec la structure de WhitesMove, nous nous sommes déjà rencontrés. La structure de BlacksMove est un peu plus simple, car il n'est pas nécessaire d'y stocker le dernier mouvement de Black.struct BlacksMove
{
public Combo combo;
public byte moves;
}
Premièrement, dans la «ligne noire», nous placerons toutes les positions mates dans lesquelles le mouvement est noir. Ensuite, à partir de chacune de ces positions, nous effectuerons un mouvement inverse pour les Blancs et formerons une "ligne blanche" - une liste de positions dans lesquelles les Blancs se déplaceront.Ces étapes devront être répétées jusqu'à épuisement de toutes les combinaisons possibles.L'algorithme principal sous forme de pseudo-code: " ", " ", " "
" "
{
" "
" "
" "
" "
" "
" "
" "
" "
" "
} " "
" "
Position mate
La création de la base des bons mouvements commence par une recherche de toutes les combinaisons de mattes. L'utilisation d'énumérateurs a permis de décrire assez efficacement ce processus. foreach (Combo combo in AllCheckmates())
{
BlacksMove checkmate = new BlacksMove { combo = combo, moves = 0 };
blackQueue.Enqueue(checkmate);
}
Total a trouvé 232 positions mates. Permettez-moi de vous rappeler que nous nous sommes limités uniquement à un éléphant à fond blanc.Certains d'entre eux sont assez exotiques, inexistants et «coopératifs», c'est alors que le roi noir lui-même est monté sous le tapis.
Les joueurs d'échecs savent très bien qu'un tapis avec un cheval et un éléphant à fond blanc doit être placé dans un coin blanc. Dans le coin noir, échec et mat n'est possible que si le noir joue avec. J'ai spécialement posté une photo avec un tel pseudo-automate au début de l'article afin de provoquer l'attention des vrais joueurs d'échecs :)Tapis en un seul mouvement
L'étape suivante consiste à inverser le blanc. Autrement dit, pour chaque position mate trouvée, effectuez tous les reculs blancs possibles .Comment faire un mouvement inverse? Étant donné qu'aucune capture n'est prévue dans nos positions, l'algorithme est assez simple - faites n'importe quel mouvement par les Blancs, après quoi il n'y aura pas de contrôle au roi noir.Toutes les positions trouvées de cette manière peuvent déjà être mises dans la «boîte blanche», indiquant qu'il y a un mouvement avant le tapis et quel type de mouvement pour ce faire. En cours de route, nous mettons les combinaisons trouvées dans la «ligne noire».Voici à quoi ressemble cette partie de l'algorithme:
while (blackQueue.Count > 0)
{
BlacksMove black = blackQueue.Dequeue();
foreach (WhitesMove white in AllWhiteBackMoves(black))
if (!isCheck(white.combo))
if (!whiteBox.Exists(white.combo))
{
whiteBox.Put (white);
whiteQueue.Enqueue(white);
}
}
Soit dit en passant, sur le rendementyield- , , :
IEnumerable<WhitesMove> AllWhiteBackMoves(BlacksMove black)
{
foreach (WhitesMove white in AllWhiteKingMoves(black))
yield return white;
foreach (WhitesMove white in AllWhiteBishopMoves(black))
yield return white;
foreach (WhitesMove white in AllWhiteKnightMoves(black))
yield return white;
}
Un total de 920 positions de ce type ont été trouvées, voici les plus intéressantes:Mouvement cheval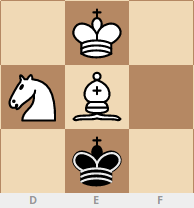
: Mouvement éléphant: Mouvement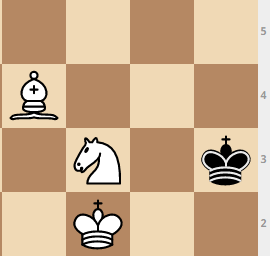
roi: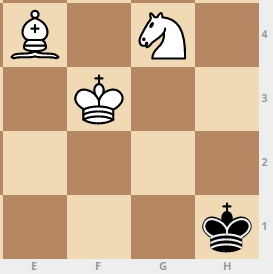
Tapis en un mouvement et demi
L'étape suivante consiste à inverser le noir. Avec cet algorithme j'ai passé le plus de temps, beaucoup d'erreurs ont été commises avant que tout fonctionne correctement.À première vue, tout est similaire à la version précédente: pour chaque position de la «ligne blanche» il faut trier tous les mouvements possibles du roi noir. Et ajoutez toutes les combinaisons trouvées à la «ligne noire» - après tout, c'est un échec et mat en un mouvement et demi, à partir duquel vous pouvez ensuite effectuer à nouveau un mouvement inverse pour les Blancs - il y aura un échec et mat en deux mouvements - et continuer jusqu'à ce que toutes les options soient révisées.C'était l'erreur. Avec n'importe quel mouvement possible, Black obtient un échec et mat matelassé «coopératif» en un mouvement et demi, mais en réalité le roi ne passera pas nécessairement sous l'échec et mat. Dmitry Grin m'a signalé cette erreur, qui a assisté à tous mes webinaires sur la création de ce programme, pour lesquels je le remercie séparément.L'algorithme correct est le suivant: pour chaque position N après le mouvement inverse du roi noir, vous devez passer par tous les mouvements directs possibles de celui-ci pour vous assurer qu'ils mènent tous à des positions familières à partir de la "boîte blanche", c'est-à-dire conduire au tapis. Et seulement après cette position, N peut être ajouté à la «ligne noire». Et si le roi noir peut «s'échapper» de la position N, alors nous sautons cette option. Elle se réunira lors des itérations suivantes, lorsqu'il y aura des postes plus familiers.Voici à quoi ressemble cette partie de l'algorithme:
while (whiteQueue.Count > 0)
{
WhitesMove white = whiteQueue.Dequeue();
Combo whiteFigures = white.combo;
foreach (BlacksMove black in AllBlackBackMoves(white))
{
bool solved = true;
foreach (Coord blackKing in AllKingMoves(black.combo.blackKing))
{
whiteFigures.blackKing = blackKing;
if (isCheck(whiteFigures))
continue;
if (box.Exists(whiteFigures))
continue;
solved = false;
break;
}
if (solved)
blackQueue.Enqueue(black);
}
}
Au total, 156 combinaisons de «mouvements mat et demi» ont été trouvées.À mi-parcours itératif
Les algorithmes décrits pour créer des demi-passes doivent être bouclés. À partir de la «ligne noire», nous formons la «ligne blanche», et vice versa - à partir de la ligne «blanche», nous formons la «ligne noire». Et ainsi de suite jusqu'à épuisement de toutes les nouvelles positions. La «boîte blanche» est remplie au stade de la formation de la «ligne blanche», car elle place les positions dans lesquelles les blancs se déplacent.L'algorithme prêt à l'emploi pour l'énumération de toutes les options a fonctionné quelque part en 12 minutes et s'est arrêté au mouvement 33. C'est le nombre de mouvements maximum nécessaires pour accoupler le roi noir avec un cheval et un éléphant de n'importe quelle position.Soit dit en passant, il n'y avait pas tellement de postes «les plus difficiles», seulement 156, en voici un:
Mata ne le sera pas!
Il existe de nombreuses positions dans lesquelles, même après le mouvement des Blancs, le roi noir peut manger un chevalier ou un évêque et obtenir un match nul. Il existe également des options de blocage. Voici quelques-uns des articles les plus intéressants.
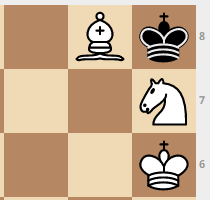
Comment stocker une base de données de solution
Comment stocker la base de solutions trouvée?La manière la plus simple et la plus fausse est d'utiliser la sérialisation. Le tableau en quatre dimensions sérialisé de la structure a pris 1,7 gigaoctets (!) D'espace disque. Le processus de sérialisation a duré environ six minutes, la désérialisation a pris environ la même chose.Cette option, bien sûr, ne convient pas. De plus, en pratique, il n'est pas nécessaire d'utiliser la totalité du réseau à quatre dimensions. Une seule entrée est nécessaire pour un élément de campagne spécifique.Eureka! Pour économiser de l'espace, vous pouvez toujours vous débarrasser du stockage des coordonnées des chiffres pour chaque combinaison. Lorsque nous avons un tableau à quatre dimensions, la position de chaque figure sur la carte est uniquement déterminée par son indice dans le tableau.Il a été décidé de stocker l'intégralité de la base de données de solutions dans un seul fichier - sous la forme d'un balayage linéaire d'un tableau à quatre dimensions. Pour toute position possible, l'adresse est calculée à laquelle la bonne réponse est enregistrée.Comment enregistrer la réponse dont nous avons besoin de manière aussi compacte que possible? La position des figures n'a pas besoin d'être stockée, il ne reste donc que trois chiffres - combien de mouvements vers le tapis, quoi aller et où aller. C'est ainsi que la bonne décision pour les Blancs est déterminée de manière unique.6 bits Le nombre de déplacements vers le tapis est un entier de 0 à 33,2bits. Quelle figure marche - trois options possibles, un roi, un éléphant ou un cheval.6 bits Où va la pièce - l'indice du champ sur la carte est de 0 à 63.Ainsi, pour chaque enregistrement de décision, deux octets suffisent:1 octet - combien de mouvements vers le tapis, ou 0 si la position n'est pas familière.2 octets - FFNNNNNNFF - numéro de la figure à marcher (1 - roi, 2 - éléphant, 3 - cheval)NNNNNN - coordonnée cellulaire - où aller (de 0 à 63).Ainsi, le fichier de base de données de solution prend 64 * 32 * 64 * 64 mots = exactement 16 mégaoctets. La position des chiffres est définie par les coordonnées de chaque mot, dans le premier octet - le nombre de mouvements vers le tapis (ou 0 s'il n'y a pas de solution), le deuxième mouvement stocke le mouvement correct.Il serait possible de réduire la taille du fichier de moitié si vous ne stockiez pas le nombre de coups sur le tapis, mais ce ne serait pas intéressant de jouer comme ça.Coordonnées de l'éléphant blanc au carré noir
Il est temps de payer pour l'optimisation. Il est nécessaire de mettre en œuvre un algorithme de recalcul des coordonnées pour les combinaisons avec un éléphant «noir et blanc».Cela a été fait comme suit. Si les coordonnées de l'éléphant tombent sur un champ noir, alors les coordonnées de toutes les figures du tableau doivent être "inversées". Dans ce cas, la coordonnée Y reste inchangée et X passe à 7-X. Une démonstration visuelle d'un retournement de coordonnées, voir la figure.
Si l'éléphant est debout sur une cage blanche, vous devez d'abord "inverser" les coordonnées de toutes les figures. Recherchez ensuite une position dans la base de données des solutions. Et encore une fois «retournez» la coordonnée du mouvement correct lu à partir de là.Visualisation de la base de solution
Donc, le problème est résolu!La base de données des solutions a été créée.Mais comment le démontrer?La façon la plus évidente est d'utiliser les technologies Web pour pouvoir simplement donner un lien vers un exemple de travail. Sur ma "formule de programmeur", le cours photo " Nano-Chess " a déjà été créé , où en utilisant les technologies HTML, CSS, JavaScript et PHP un échiquier interactif a été créé pour jouer sans règles à deux. Ce script a été pris comme base.Je n'ai laissé que quatre morceaux, supprimé la possibilité de capture, ajouté des fonctions PHP pour lire les mouvements corrects de la base de la solution et «respiré la vie» via JavaScript.Sur la page www.videosharp.info/chess, vous pouvez expérimenter avec la base de données de solutions.
Pour chaque position, les déplacements sont calculés pour le blanc et le noir.Pour les blancs - le meilleur coup qui mène à l'échec et mat.Pour le noir - combien de mouvements vers le tapis pour tout mouvement possible.Vous pouvez faire n'importe quel mouvement des figures avec la souris, pas nécessairement selon les règles.Le script calculera l'option pour n'importe quelle position, ou notera qu'il n'y a pas d'options.Il est intéressant de jouer, d'effectuer les mouvements proposés ou de déplacer les pièces à votre discrétion.Conclusion
Un excellent travail intéressant a été fait pour résoudre le problème des échecs.Si vous souhaitez répéter de cette façon, vous pouvez regarder des vidéos sur la création de ce programme de zéro au résultat avec des explications détaillées et des tâches indépendantes.Bonne chance!