🐉 ♥️ 👨🏼‍🔧 On se met en forme: de la géométrie hyperbolique aux complexes cubiques et vice versa 🚰 🖇️ 🍹

La preuve marque la fin d'une époque dans l'étude des formes tridimensionnelles.

Il y a trente ans, le mathématicien William Thurston parlait de sa vision: systématiser toutes les formes tridimensionnelles finies possibles.

Thurston, le lauréat du Fields Prize qui a passé la majeure partie de sa carrière dans les universités de Princeton et Cornell, avait une capacité surnaturelle de représenter l'inimaginable: non seulement les formes vivant dans un espace tridimensionnel ordinaire, mais aussi une ménagerie beaucoup plus grande de formes ayant des propriétés si complexes qu'elles ne peuvent s'adapter que dans espace avec beaucoup de dimensions. Là où d'autres mathématiciens ont vu les débuts des formes, Thurston a vu des structures: symétries, surfaces, relation entre différentes figures.

William Thurston à Berkeley en 1991.

«Après de nombreuses années d'études, de nombreuses personnes ont l'impression que les mathématiques sont un sujet strict et formel qui traite de règles complexes et obscures», écrivait-il en 2009. "Les bonnes mathématiques sont exactement l'opposé de cela." Les mathématiques sont l'art de la compréhension humaine ... Les mathématiques chantent quand nous le ressentons avec tout notre cerveau. »

La vision de Thurston était basée sur un mariage entre deux approches apparemment disparates de l'étude des figures tridimensionnelles: la géométrie, un royaume familier d'angles, de longueurs, de régions et de volumes, et une topologie qui étudie les propriétés des formes qui sont indépendantes de mesures géométriques précises - des propriétés qui ne sont pas changer si la forme est étirée ou tordue, comme une " poignée ".

Pour un topologue, la surface de la casserole est équivalente à la surface d'une table, d'un crayon ou d'une balle; la surface de la coupe équivaut à un beignet ou un tore. Du point de vue d'un topologue, la variété des formes bidimensionnelles - surfaces - se résume à une simple liste de catégories: sphériques, toroïdales et toroïdales avec un grand nombre de trous. (La plupart d'entre nous présentent les sphères et les tores comme tridimensionnels, mais comme les mathématiciens les considèrent comme des surfaces creuses, ils considèrent ces surfaces comme des objets bidimensionnels, mesurés par leur surface et non par leur volume).

L'idée clé de Thurston était de comprendre les 3 variétéspossible grâce à l'union de la géométrie et de la topologie. De la même manière que la catégorie topologique des 2 variétés, contenant la surface d'une poêle et d'un crayon, contient également une sphère idéale, Thurston a suggéré que de nombreuses catégories de 3 variétés contiennent une instance, une 3 variétés dont la géométrie est si homogène et parfaite, si belle que, comme l’a dit Walter Neumann de l’université de Columbia, elle «sonne comme une cloche». De plus, Thurston a suggéré que les formulaires qui n'ont pas une telle instance peuvent être découpés en morceaux dans lesquels ils le seront déjà.

Dans un article de 1982, Thurston a avancé son «hypothèse de géométrisation» parmi 23 questions sur les variétés 3 qui offraient aux mathématiciens la direction de la connaissance des formes tridimensionnelles. (Il y avait 24 questions sur la liste, mais l'une d'entre elles, toujours non résolue, ressemble plus à une ruelle intrigante qu'à la route principale).

«Thurston avait un énorme talent pour poser les bonnes questions», explique Vladimir Markovich, un mathématicien de Caltech. "Tout le monde peut poser des questions, mais il arrive rarement qu'une question mène à des idées et à la beauté, tout comme les questions de Thurston ont réussi."

Les questions ont inspiré une nouvelle génération de mathématiciens, dont des dizaines ont décidé de mener leur travail sous la direction de Thurston. Ses «enfants» mathématiques expriment son style, comme l'a écrit Richard Brown.de l'Université. John Hopkins. "Ils regardent les mathématiques, comme les enfants à une foire: avec joie et surprise, fascinés par chaque nouvelle découverte, et ils sont simplement heureux d'en faire partie."

Des dizaines d’années après l’apparition des travaux de Thurston, les mathématiciens ont suivi sa «carte» de la recherche, et leur motivation a été nourrie non pas tant par les applications possibles de leurs découvertes que par la bonne place qu'occupaient les 3 variétés dans l’étude des formes. Les formes bidimensionnelles sont assez courantes, elles sont faciles à représenter et à diviser en catégories. Les formes à quatre, cinq et plusieurs dimensions sont pratiquement impossibles à former du tout: la variété des possibilités est si grande que les mathématiciens se sont limités à ne connaître que leurs sous-classes spéciales. Et dans le cas des formes de structure tridimensionnelles, d'une part, elles sont mystérieuses et difficiles, mais d'autre part, elles sont fondamentalement reconnaissables.

Le travail de Thurston a duré 30 ans, et tous les problèmes sauf quatre ont déjà été résolus, y compris l'hypothèse de géométrisation, prouvée par le mathématicien russe Grigory Perelman en 2002, qui était une réalisation historique dans les mathématiques modernes. Mais les quatre tâches restantes ont obstinément résisté.

"Le fait que nous n'ayons pas été en mesure de les résoudre depuis si longtemps signifie que quelque chose de très profond y est caché", a déclaré Yair Minsky de l'Université de Yale.

Enfin, en mars 2012, Ian Aigol de l'Université de Californie à Berkeley a suscité la communauté des maths en annonçant la preuve de l'hypothèse Wise qui couvrait les quatre dernières questions de Thurston d'un seul coup.

Les mathématiciens appellent ce résultat la fin d'une époque.

"La vision des 3 variétés décrite par Thurston dans son travail à cette époque aurait pu sembler fantastique, mais maintenant elle est pleinement réalisée", explique Danny Calegari de Caltech. "Ses idées ont été étonnamment prouvées - et chaque détail était correct."

«Il me semblait qu'il y avait une connaissance particulière et des méthodes de pensée particulières qui m'étaient propres», a écrit Thurston, ayant reçu le prix de mathématiques Steele quelques mois seulement avant sa mort en août 2012 à 65 ans . "Et je suis très heureux d'avoir atteint un tel niveau alors que ce n'est pas le cas - beaucoup de gens ont partagé ma façon de penser, et beaucoup ont prouvé les théorèmes que j'ai entrepris sans succès."

La réalisation d'Aigol montre l'existence d'un schéma simple pour construire toutes les variétés hyperboliques compactes à 3 - le seul type de formes tridimensionnelles qui n'a pas encore été entièrement expliqué.

«Nous comprenons maintenant exactement à quoi ressemblent tous les 3 collecteurs», a déclaré Henry Wilton du London University College. «C'est l'aboutissement d'une énorme réussite mathématique.»

Etude de surface

Le programme de Thurston a essayé de faire avec les variétés 3 ce que les mathématiciens ont fait avec succès il y a cent ans avec les variétés bidimensionnelles. Pour nous étirer avant de comprendre les variétés tridimensionnelles, jetons un œil à l'intérieur de la classification des surfaces «compactes orientables» (surfaces finies sans perforations et coupes avec une orientation constante).

Pour aborder le problème de classification, les mathématiciens ont montré que pour n'importe quelle surface, il est possible d'effectuer sa simplification séquentielle en la coupant le long des courbes jusqu'à ce qu'elle s'ouvre en un polygone plat.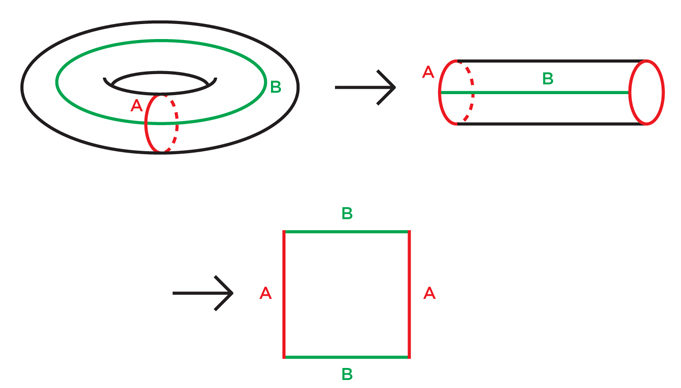

Fig. 1

Il est facile de le montrer pour un tore: nous le coupons d'abord le long de la boucle A, comme sur la figure 1, nous obtenons un cylindre. Ensuite, nous coupons le long de la boucle B, redressons le cylindre en carré. La figure 2 est un peu plus difficile à comprendre, mais même là, couper le long de quatre courbes transforme un double tore (un tore à deux trous) en octogone. De la même manière, pour tout tore à n trous, on peut faire 2n encoches dans les boucles et l'étendre en 4n-gon.

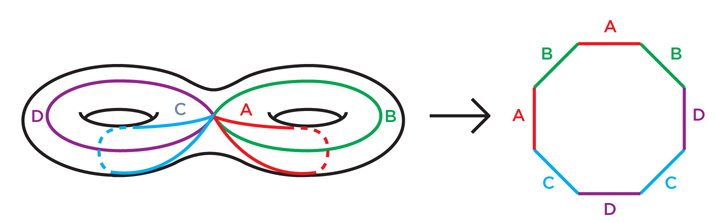Fig.2

Vous pouvez essayer de simplifier une surface indéfinie arbitraire (et l'identifier) en la coupant de la même manière. S'il ne s'agit pas d'une sphère, les topologues ont montré qu'elle devrait contenir des boucles internes (boucles qui ne se coupent pas) qui ne peuvent pas être tirées en un point - comme A et B sur le tore. Couper une surface le long de l'une de ces boucles supprime plusieurs propriétés topologiques intéressantes de la surface. Les mathématiciens ont montré que pour réduire la surface en un polygone plat, il est nécessaire de la couper un nombre fini de fois.

Après avoir simplifié la surface au niveau du polygone, il est facile de voir que si nous collons ses bords pour restaurer la surface d'origine, nous devrons faire un tore, ou un double tore, ou un triple tore, etc. Après tout, le premier collage transformera le polygone en surface de la vue du tunnel, et chaque suivant ajoutera un nouveau tunnel ou coudra simplement des parties ouvertes. Lorsque nous terminons le processus, nous obtenons un tore avec quelques trous.

Une telle approche démontre non seulement l'équivalence topologique d'une surface à une sphère ou à un tore: elle fournit également un moyen de doter une surface d'une structure géométrique simple et uniforme.

La sphère, évidemment, a déjà une structure géométrique unifiée: sa géométrie est la même depuis n'importe quel endroit de la sphère. La surface du beignet, au contraire, n'est pas du tout uniforme: la région du bord extérieur du beignet est courbée d'une manière similaire à une sphère, et la région de l'anneau intérieur est courbée comme une selle.

Et peu importe la façon dont vous placez le tore dans l'espace - peu importe la façon dont vous l'étirez et le tordez - vous ne pouvez pas faire en sorte que la géométrie soit la même partout. Certaines parties arrondiront comme une sphère, d'autres comme une selle, d'autres peuvent être plates.

Il est cependant possible d'équiper le tore d'une structure géométrique abstraite identique en tout point - il suffit de déclarer que sur chacune des petites sections du tore, les distances et les angles sont déterminés en mesurant le carré à partir duquel, comme nous l'avons vu, le tore peut être réalisé. Un tore physique dans l'espace ordinaire, dont les longueurs et les angles correspondent à cette règle abstraite, ne peut pas être construit, mais cette définition des longueurs et des angles est cohérente en interne. Puisque le carré a la géométrie plate (euclidienne) habituelle, nous disons que le tore peut être équipé d'une structure euclidienne. Un tore avec une telle géométrie ressemble à un jeu vidéo dans lequel un personnage disparaît du côté gauche de l'écran et réapparaît à droite, et disparaît du côté supérieur, apparaît en bas.

En essayant de faire cette opération avec un double tore, nous rencontrerons un obstacle. N'oubliez pas que nous pouvons faire un double tore en collant les bords d'un octogone. Si nous déclarons que la géométrie du double tore est de copier la géométrie de l'octogone, nous rencontrerons le problème de ses angles. Après avoir collé l'octogone en un double tore, les points d'angle seront collés ensemble, en un point du double tore. Il y aura huit angles à ce stade, chacun ajoutera 135 degrés, qui ensemble seront de 1080 degrés au lieu de 360.

Si nous essayons de donner la structure géométrique de l'octogone au double tore, il s'avère que notre double tore aura partout la géométrie euclidienne habituelle, sauf pour un point où sa surface fait saillie comme un chapeau pointu (les points d'angle ne sont pas un problème si nous collons un carré dans un tore: nous collons quatre angles droits et obtenez les 360 degrés parfaits).

Pour obtenir une structure géométrique lisse au point d'angle du double tore, il faut que chacun des huit angles ne contribue qu'à 45 degrés au lieu de 135. Il est intéressant qu'un tel octogone existe, mais ne vit pas dans le plan euclidien habituel, mais sur une autre structure appelée disque hyperbolique: le troisième un type de géométrie qui est uniforme et cohérent en interne, comme sphérique ou euclidienne. Mais comme il est plus difficile à imaginer, il n'a été découvert par les mathématiciens qu'au début du XIXe siècle.

Fig.3

En gros, la géométrie hyperbolique (ou géométrie Lobachevsky) est obtenue si nous déclarons que tous les poissons de la figure 3 sont de la même taille. On peut imaginer que la figure 3 est en fait une image disque obtenue à travers une lentille déformante, ce qui rend le poisson plus près du bord plus petit que le poisson au milieu. Sur un véritable disque hyperbolique devant l'objectif, tous les poissons sont de la même taille.

Dans l'espace ordinaire, il est impossible de faire un disque hyperbolique régulier et lisse afin que tous les poissons soient vraiment les mêmes. Mais d'un point de vue abstrait, la règle de la taille du poisson donne une géométrie qui est cohérente en interne et qui a la même apparence en tout point - pas pour un observateur avec une lentille déformante, mais du point de vue d'un résident d'un disque hyperbolique.

En géométrie hyperbolique, le chemin le plus court, ou «géodésique», entre deux points est le chemin à travers le plus petit nombre possible de poissons. Un tel chemin est toujours un demi-cercle perpendiculaire à la limite du disque. Les demi-cercles qui longent les épines des poissons en sont des exemples. De notre point de vue déformé, ces chemins sont courbes, mais pour un résident du disque ce sont des lignes droites. Comme l'a dit Thurston, pour la conduire, il n'est pas nécessaire de tourner le volant. Contrairement au plan euclidien, sur lequel les lignes parallèles restent toujours à la même distance, sur un disque hyperbolique deux lignes disjointes peuvent très rapidement s'écarter l'une de l'autre.

Du point de vue de la géométrie hyperbolique, les figures de la figure 4 sont des octogones ordinaires à côtés droits. Dans l'un de ces octogones, tous les angles à 45 degrés sont exactement ce dont nous avons besoin pour un double tore. Si nous collons correctement les côtés de cet octogone, nous obtenons un double tore avec une structure hyperbolique idéale et uniforme.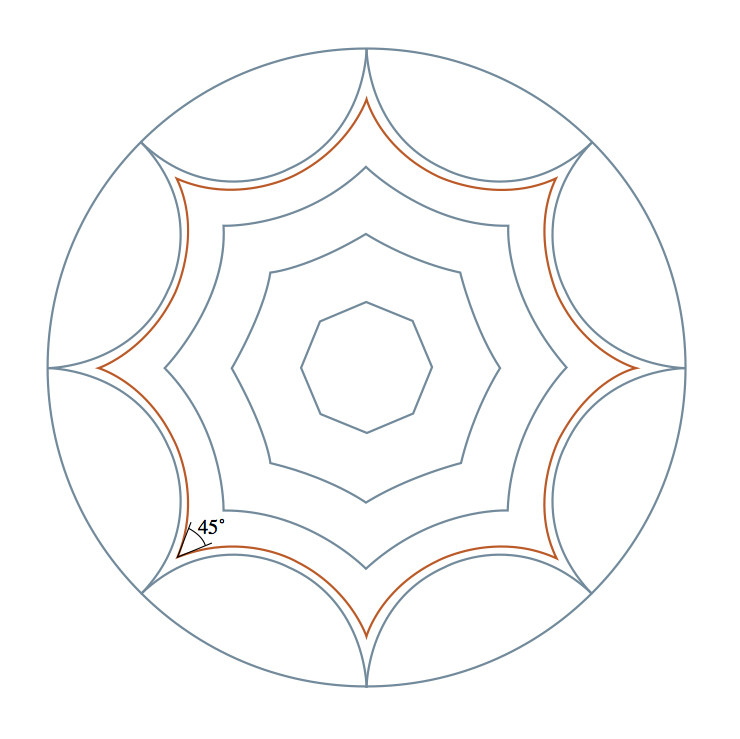

Fig.4

De la même manière, nous pouvons équiper le triple tore d'une structure hyperbolique. Le triple tore peut être collé à partir d'un 12-gon, donc si nous faisons un 12-gon hyperbolique avec des angles internes de 30 degrés, sa géométrie hyperbolique peut être transférée en douceur au triple tore. Poursuivant le thème, nous pouvons fournir un tore à 4 trous, avec le 5e et ainsi de suite, la géométrie hyperbolique. Notre classification des surfaces compactes est la suivante: une surface à géométrie sphérique (sphère), une à euclidienne (tore) et une infinité de surfaces à géométrie hyperbolique (toutes des tores à plus d'un trou).

Au cours des cent dernières années, cette classification a donné aux mathématiciens une méthode très fructueuse de transfert des questions topologiques sur les surfaces dans le domaine géométrique, et vice versa. La classification des surfaces est l'idée principale dans l'étude des formes bidimensionnelles, une découverte utilisée par toutes les autres études comme point de départ.

Mesure suivante

Les 3 variétés sont beaucoup plus diverses que les 2 variétés et les problèmes avec elles sont plus compliqués. Même une question simple comme la célèbre conjecture de Poincaré - qui demande si la version tridimensionnelle de la sphère est la seule forme tridimensionnelle compacte sur laquelle chaque boucle peut être tirée en un point sans accrocher le trou - est restée non résolue pendant près de cent ans après sa formulation par Henri Poincaré en 1904 année.

Mais Thurston a hardiment suggéré qu'il est possible de créer une classification des formes tridimensionnelles similaire à la classification existante des formes bidimensionnelles.

Les géométries euclidiennes, sphériques et hyperboliques bidimensionnelles ont des paires en trois dimensions. Mais en trois dimensions, la liste des «belles» géométries ne s'y limite pas. Il existe des géométries hybrides hyperboliques ou sphériques dans certaines directions et euclidiennes dans d'autres. En général, il existe huit types de géométries différentes en trois dimensions, uniformes dans le sens où la géométrie est la même à n'importe quel point de l'espace.

Thurston a suggéré que, comme pour les surfaces, les 3 variétés peuvent être comparées aux structures géométriques naturelles. Plus précisément, il a suggéré que si vous coupez n'importe quel 3-collecteur compact en morceaux d'une manière spéciale, chaque pièce peut être associée à l'une des huit géométries.

«L'objectif était d'unifier complètement la topologie et la géométrie en trois dimensions», explique Minsky.

L'approche naturelle de cette «hypothèse de géométrisation» était d'essayer quelque chose de similaire à ce que nous avons fait avec les surfaces que nous coupons le long des courbes jusqu'à ce qu'elles révèlent toutes les propriétés topologiques intéressantes, et jusqu'à ce qu'elles se simplifient en un polygone plat. Pour les 3 collecteurs, une approche similaire consistera à les couper le long des surfaces jusqu'à ce, espérons-le, qu'ils se simplifient en un polyèdre, dont les côtés opposés peuvent être collés ensemble pour obtenir la forme d'origine. Et si nous pouvons construire ce polyèdre en utilisant la géométrie correcte, nous pouvons transformer cette géométrie à sa forme d'origine, comme c'était le cas avec les surfaces.

Rappelez-vous que dans le cas des surfaces, chaque courbe devait satisfaire deux exigences: la courbe ne se croise pas avec elle-même (les mathématiciens disent qu'elle devrait être «incrustée»), et elle devrait être, comme nous l'appelons, topologiquement intéressante, c'est-à-dire entourer le détail topologique de la surface afin qu'elle ne puisse pas être tirée jusqu'à un point (cette exigence garantit que la coupe le long de cette courbe simplifie la topologie de la surface).

En 1962, le mathématicien Wolfgang Haken a prouvé qu'un 3-collecteur peut être simplifié en un polygone si le 3-collecteur contient une surface dont la coupe satisfait à deux conditions: il doit être encastré et «incompressible», c'est-à-dire tout intérêt topologique une courbe en surface sera également topologiquement intéressante dans le contexte plus général du 3-collecteur environnant.

Par exemple, un tore ne sera pas incompressible dans un espace tridimensionnel ordinaire, car la boucle passant par l'ouverture du tore est topologiquement intéressante du point de vue de la surface du tore, mais dans un espace tridimensionnel, elle peut être compressée en un point. Inversement, un tore est incompressible à l'intérieur d'un collecteur 3, ce qui peut être obtenu en épaississant la surface du tore de sorte qu'il cesse d'être infiniment mince. Pour être incompressible, chaque caractéristique topologique de la surface doit refléter une topologie interne du 3-collecteur. Désormais, un manifold à 3 composants avec une surface incompressible intégrée est appelé manifold de Haken.

Si notre collecteur à 3 a une surface incompressible intégrée, le découper le long révélera des topologies intéressantes et nous donnera un collecteur simplifié. De plus, Haken a montré que si un collecteur contient une telle surface, le nouveau collecteur obtenu en le coupant sera également un collecteur Haken: il aura également une surface de coupe incompressible intégrée. Et après un nombre fini de telles étapes, comme l'a montré Haken, toutes les caractéristiques topologiques intéressantes du collecteur d'origine seront coupées, et un simple polyèdre restera.

À la fin des années 1970, Thurston a montré qu'il était possible d'équiper le polyèdre résultant avec l'une des huit géométries à huit dimensions de manière à ce qu'il se transfère en douceur vers le polygone nouvellement collé, parfaitement assorti aux coins et aux bords du polyèdre. En d'autres termes, Thurston a prouvé son hypothèse de géométrisation pour les variétés dont la décomposition standard conduit à des pièces qui sont des variétés de Haken.

Malheureusement, pour un collecteur 3 arbitraire compact, il n'y a aucune garantie qu'il ait une telle surface. À la fin des années 1970 et au début des années 1980, Thurston a convaincu la communauté que les 3 variétés contenant une surface incompressible intégrée (variétés de Haken) sont des exceptions, pas des règles.

La recherche de la preuve de l'hypothèse de géométrisation pour des variétés autres que les variétés de Haken bloque les mathématiciens depuis plus de vingt ans. Enfin, en 2002, Perelman a présenté sa preuve basée sur des domaines mathématiques très éloignés de ceux étudiés par la plupart des adeptes de Thurston. (Ressembler à la preuve de Perelman a également touché l'hypothèse centenaire de Poincaré, ce qui a conduit Clay's Mathematics Institute à lui offrir un prix d'un million de dollars en 2010 - qu'il a rejeté tout de suite pour des raisons complexes).

La preuve de Perelman a été un tournant, combinant, comme le rêvait Thurston, la topologie et la géométrie. Maintenant, chaque problème topologique associé à 3 variétés a une paire géométrique, et vice versa. Mais le théorème de Perelman n'a pas résolu de nombreuses questions importantes sur les types de 3 variétés possibles.

En classant les 2 collecteurs compacts (surfaces), les mathématiciens pourraient non seulement montrer que chaque surface peut être équipée d'une structure géométrique, mais aussi faire une liste complète de tous les 2-collecteurs possibles. En trois dimensions, une telle liste faisait cruellement défaut.

Sept des huit géométries tridimensionnelles - toutes sauf hyperboliques - étaient bien connues, et même avant les travaux de Perelman, les topologues ont compilé une description complète des types de variétés qui admettent l'une de ces sept géométries. Ces formulaires sont relativement simples et peu nombreux.

Mais, comme dans le cas des surfaces, en trois dimensions, il s'est avéré que la plupart des variétés sont hyperboliques. Et la couverture d'un grand nombre de possibilités de variétés 3 hyperboliques était bien pire chez les mathématiciens que pour les sept autres géométries.

"Sur les huit types de géométries, les variétés hyperboliques sont les plus mystérieuses et les plus riches", explique Nicolas Bergeron de l'Université Pierre et Marie Curie à Paris.

Le résultat de Perelman a dit aux mathématiciens que les variétés hyperboliques étaient la dernière frontière - le seul type de 3 variétés qui restait à comprendre. Mais il ne leur a pas dit à quoi ressemblaient ces formes hyperboliques.

Histoire de couverture

Une fois de plus, les mathématiciens ont pu se tourner vers le travail de Thurston pour obtenir des conseils. Sa célèbre liste de questions contenait de nombreuses hypothèses sur les propriétés des variétés hyperboliques 3, qui comprenaient deux hypothèses directement liées à leur apparence: l'hypothèse «Haken virtual» et l'hypothèse «bundle virtuel».

L'hypothèse virtuelle de Haken (HHC) stipule que chaque variété hyperbolique compacte 3 est presque une variété de Haken dans un certain sens: il est possible de transformer la variété en une variété de Haken en augmentant son nombre fini de fois d'une certaine manière. Ce nouveau collecteur déplié est appelé «couvercle fini» du collecteur d'origine.

Les mathématiciens disent qu'une variété N couvre une autre variété M, si, grosso modo, il est possible d'enrouler N autour de M un certain nombre de fois (éventuellement infini) pour que chaque partie de M soit recouverte autant de fois que les autres. Pour être une couverture, cette enveloppe doit avoir un tas d'autres propriétés - par exemple, N ne doit pas se plier sur lui-même, ni se déchirer pendant l'emballage. Chaque morceau de M est recouvert d'un tas d'exemplaires identiques en N. le recouvrant.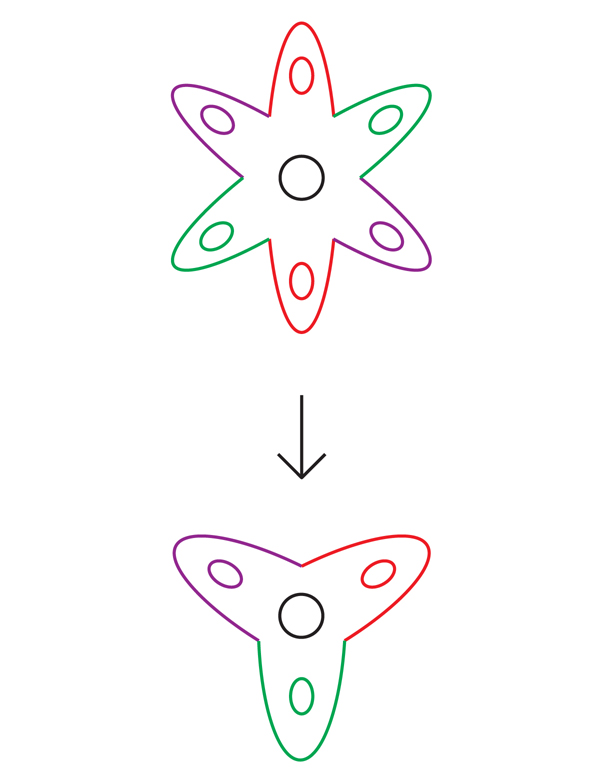

Fig . 5

Par exemple, la fleur à six pétales de la Fig. 5 couvre une fleur à trois pétales: il suffit d'enrouler la fleur à six pétales deux fois autour des trois pétales. Chaque point de couleur à trois pétales est recouvert de deux points de six pétales. Les mathématiciens appellent cela un revêtement à deux couches.

De la même manière, un cylindre infini recouvre le tore: il suffit d'enrouler le cylindre autour du tore un nombre infini de fois (Fig. 6). Chaque point du cylindre est couvert: la boucle A est couverte par un ensemble infini de boucles réparties uniformément sur le cylindre, et la boucle B est déployée sur le cylindre en ligne le long.

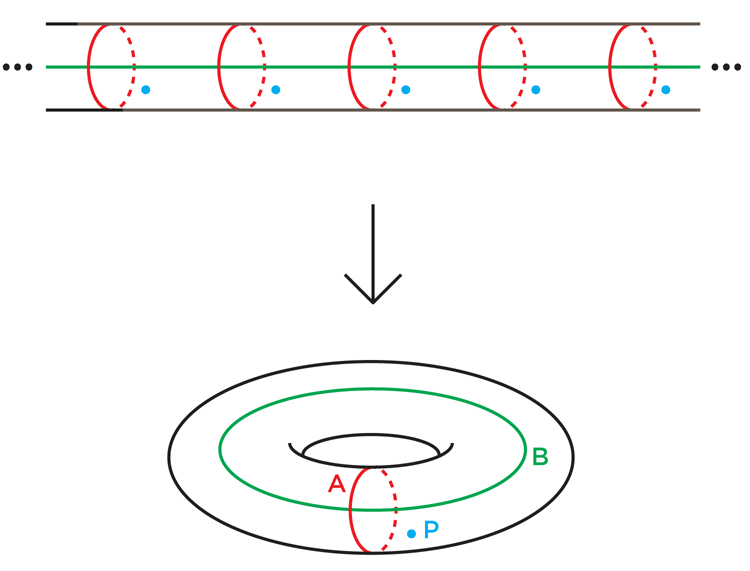Fig. 6 Les

topologies de la diversité et ses couvertures sont étroitement liées. Pour recréer un collecteur à partir d'un revêtement à n couches, il vous suffit de plier le revêtement par lui-même n fois. Et vice versa, afin de recréer le revêtement sur la base de la variété, vous le coupez, faites n copies et le collez le long des bordures (le revêtement en béton que vous avez reçu dépend du choix de la séquence de collage).

Un revêtement préserve certaines propriétés topologiques d'un collecteur et en révèle d'autres. Un cylindre infini, par exemple, se souvient que la boucle A sur le tore est fermée, mais oublie que la boucle B est également fermée.

Ce processus de déploiement a conduit Thurston à espérer que pour un collecteur à 3, il est possible de couvrir avec un nombre fini de couches, qui sera un collecteur de Haken. Nous avons déjà souligné qu'il ne faut pas s'attendre à ce qu'un collecteur hyperbolique compact arbitraire 3 soit un collecteur de Haken (qu'il aura une surface incompressible intégrée). Mais en 1968, le mathématicien allemand Friedhelm Waldhausen a suggéré qu'un tel collecteur devrait au moins contenir une surface incompressible, bien qu'il puisse passer à travers lui-même et ne pas être encastré.

Dans l'affirmative, selon Thurston, il pourrait y avoir un revêtement final dans lequel la surface se déplie d'une manière qui élimine toutes les auto-intersections. Les revêtements finis sont souvent simplifiés de cette manière. Par exemple, étant donné que la courbe de la fleur à trois pétales de la figure 7 fait deux fois le tour du trou central, aucun étirement et décalage ne peuvent l'empêcher de se croiser avec elle-même. Mais si nous tournons cette courbe sur une fleur à six pétales, à partir d'un certain point P, la courbe rouge résultante (que les mathématiciens appellent la "montée" de la courbe d'origine) ne fera le tour du trou central qu'une seule fois et ne se coupera pas avec elle-même. (Il y a aussi une deuxième montée, une courbe bleue traversant le rouge en deux points, fermant le point d'intersection dans une fleur à trois pétales).

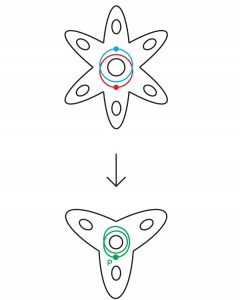Fig. 7

Dans un article de 1982, Thurston a suggéré que si nous avons un collecteur 3 hyperbolique compact, il doit y avoir un moyen de l'étendre afin que nous ayons des surfaces intégrées dans le revêtement fini - c'est-à-dire que le 3 collecteur devrait être «virtuellement Haken».

Comme nous l'avons déjà vu, une variété de Haken peut être construite en collant les limites des faces d'un polyèdre d'une certaine manière. Le VGH implique que tout collecteur 3 hyperbolique compact peut être construit en collant d'abord correctement le polyèdre, puis en enroulant la forme résultante autour d'elle un nombre fini de fois.

Thurston a fait une hypothèse encore plus stricte: que chaque collecteur hyperbolique compact 3 peut être virtuellement stratifié, c'est-à-dire avoir un revêtement stratifié fini. Une variété qui «stratifie sur un cercle» (comme disent les mathématiciens) est construite en épaississant légèrement la surface, ce qui la rend tridimensionnelle, et en collant les bordures intérieure et extérieure ensemble de toute manière qui assure une connexion lisse des surfaces en chaque point. (Un tel collage est impossible dans l'espace ordinaire sans l'intersection des parties de la variété résultante entre elles, mais de manière abstraite, il peut encore être étudié). On dit que la stratification des variétés est, car il est possible d'imaginer comment une surface épaissie est étirée de sorte que les surfaces limites divergent loin les unes des autres,puis dépliez-les et tirez-les l'un vers l'autre avant de les coller, et la variété résultante ressemble à un bracelet avec une perle infiniment mince en forme de surface à chaque point du fil du bracelet. Ces perles sont des couches.

Chaque collecteur en couches est un collecteur Haken, mais pas l'inverse. Par conséquent, l'hypothèse des bundles virtuels est plus forte que VGH, et Thurston n'était pas sûr que ce soit vrai. "Cette question discutable, apparemment, a une chance certaine d'obtenir une réponse positive", est tout ce qu'il a pu écrire dans un ouvrage de 1982.

Thurston a initialement déclaré le VGH dans une première tentative pour approcher son hypothèse de géométrisation, qu'il avait déjà prouvée pour les variétés 3 de Haken. Si le VGH était vrai et que chaque collecteur compact 3 était un revêtement fini Haken, alors peut-être (espérait Thurston) il serait possible d'utiliser la structure de revêtement géométrique pour construire la structure géométrique du collecteur d'origine.

30 ans plus tard, bien plus tard que Perelman a prouvé l'hypothèse de géométrisation par des méthodes complètement différentes, l'hypothèse VGH et le faisceau virtuel sont restées non prouvées. Elles, ainsi que deux autres hypothèses les concernant, sont restées les seules questions sans réponse sur 23. Les calculs informatiques ont plaidé en faveur de la validité des revêtements finis VGH - Haken ont été trouvés pour chacune des 10 000 variétés 3 hyperboliques sélectionnées par ordinateur. Ce travail a été réalisé par Thurston et Nathan Dunfield de l'Université de l'Illinois à Urbana-Champaign. Mais la destruction informatique n'est pas une preuve.

«Lorsque Thurston a avancé cette hypothèse virtuelle de Haken, cette question semblait facile. Mais il a obstinément résisté à la décision, qui a mis en lumière le peu que nous comprenons dans ce domaine, a déclaré Minsky. "Il s'est avéré que notre ignorance dans cette direction était profonde."

Surfaces de construction

En 2009, les eaux troubles entourant le stockage eau-eau ont commencé à être purifiées. Cette année-là, Markovich et Jeremy Kahn, qui travaillaient alors à l'Université de Stony Brook, ont annoncé la preuve d'une étape clé vers la preuve de la VHC. Le résultat, que nous appellerons le «théorème sur les surfaces incompressibles», postule que chaque variété hyperbolique compacte à 3 contient une surface incompressible (qui, éventuellement, se croise avec elle-même et n'est pas encastrée).

La preuve de Kan et Markovich est l'un des exemples centraux de l'interaction de la topologie et de la géométrie tridimensionnelles: le théorème sur les surfaces incompressibles est une déclaration purement topologique, mais Kan et Markovich ont activement utilisé une autre structure tirée de la géométrie hyperbolique pour le prouver.

Pour construire la surface à l'intérieur de la variété 3, Kahn et Markovich ont utilisé la propriété des formes hyperboliques appelées «mélange exponentiel». Cela signifie que si vous commencez un chemin quelque part dans une petite zone à l'intérieur du collecteur, choisissez une direction et imaginez que votre zone commence à se déplacer le long de la rivière qui coule approximativement dans la direction sélectionnée, votre zone se propagera progressivement et s'enroulera autour d'une 3 collecteur, elle obtiendra à n'importe quel endroit possible de n'importe quelle direction possible. De plus, il le fera très rapidement au sens exact «exponentiel».

La propriété de mélange est unique pour les variétés 3 hyperboliques et croît, en gros, du fait que, contrairement aux espaces euclidiens, dans un espace hyperbolique, les «lignes droites» ou les géodésiques sont courbées les unes par rapport aux autres. Si vous sélectionnez une petite zone d'un disque hyperbolique et lui permettez de se déplacer dans la direction sélectionnée, il se développera exponentiellement rapidement. À l'intérieur d'un collecteur compact 3, la région de croissance croîtra également de façon exponentielle, mais comme la taille du collecteur est finie, cette région finira par s'enrouler encore et encore, se chevauchant plusieurs fois. De plus - et c'est déjà plus difficile à prouver - la zone s'enroulera autour du collecteur uniformément, en passant par tous les points avec approximativement la même fréquence.

Les mathématiciens ont traité cette propriété du mélange exponentiel il y a plus de 25 ans et ont soigneusement étudié les statistiques de ce «flux géodésique», ayant approximativement découvert quand et à quelle fréquence une zone donnée passera à un certain point. Mais jusqu'à ce que Kahn et Markovich adoptent correctement le théorème de la surface incompressible, les mathématiciens ne pouvaient pas utiliser cette propriété pour construire des structures topologiques dans un collecteur (un autre mathématicien, Lewis Bowen de la Texas A&M University, a essayé d'utiliser le mélange exponentiel pour construction de surfaces incompressibles en 3 collecteurs, mais son travail a rencontré des obstacles techniques).

Pour voir comment la propriété du mélange exponentiel aide à construire des structures topologiques et géométriques, nous l'appliquons à une tâche plus simple que la construction de surfaces: construire une boucle géodésique fermée dont la longueur est proche de notre grand nombre préféré (nous la désignons par R).

Pour construire une boucle, nous sélectionnons n'importe quel point de départ dans le collecteur et n'importe quelle direction initiale, puis allumons un tuyau d'arrosage imaginaire situé dans une petite zone comprenant le point de départ et le dirige approximativement dans la direction sélectionnée. Des gouttes d'eau voleront le long du chemin géodésique, et tant que R est suffisamment grand, mélanger le flux signifiera qu'au moment où les gouttes auront dépassé la distance R, elles seront réparties à peu près également sur toute la variété. En particulier, au moins une goutte devra retourner dans la zone du point de départ. Ensuite, nous construisons simplement un petit pont reliant la géodésique de cette goutte au point de départ pour obtenir une boucle qui est presque parfaitement géodésique avec une longueur d'environ R. Il est facile de montrer qu'en resserrant cette boucle sur le collecteur,Vous pouvez obtenir la boucle géodésique parfaite.

Notez que la méthode nous donne plus d'une seule boucle géodésique proche de R. Dans ce processus, vous pouvez utiliser n'importe quel point de départ et n'importe quelle direction, vous pouvez donc faire beaucoup de telles boucles. C'est le principe de base de la construction de structures utilisant un mélange exponentiel.

Le mélange exponentiel «affirme que peu importe les structures de diversité que vous trouvez, vous les trouverez en quantité suffisante», explique Kalegari.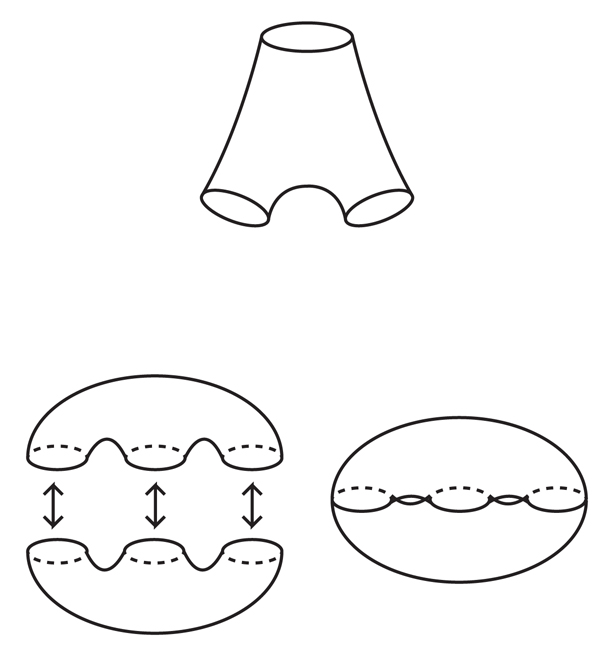

Fig. 8

Kan et Markovich ont utilisé une approche similaire à notre exercice pour créer des «paires de pantalons» - des surfaces qui sont topologiquement équivalentes à une sphère à trois trous (pour ainsi dire, une pour la ceinture et deux pour les jambes). Ces pantalons sont le matériau de départ pour la construction de toutes les surfaces compactes, à l'exception de la sphère et du tore - par exemple, le collage (ou la couture) de deux pantalons nous donne un double tore (Fig.8).

Kan et Markovich ont montré que pour un nombre suffisamment grand de R, il est possible de construire de nombreuses paires de pantalons de ce type à l'intérieur du collecteur, que leurs trois «poignets» approcheront de la longueur de R et seront presque entièrement géodésiques, c'est-à-dire que chaque morceau de la surface du pantalon aura la même apparence du point vue de la géométrie hyperbolique.

Ils ont également montré que pour tout brassard, les pantalons ont une autre paire de pantalons, allant du brassard dans la direction approximativement opposée. Assemblant ces pantalons aux poignets, Kahn et Markovic ont reçu une grande famille de surfaces compactes, presque entièrement géodésiques, avec de petites rides aux coutures. Presque les surfaces géodésiques sont incompressibles à l'intérieur de leurs 3 collecteurs; par conséquent, la construction de Kan et Markovich a prouvé le théorème des surfaces incompressibles.

Cette méthode a également montré qu'un 3-collecteur a non seulement une surface incompressible, mais «une structure riche de surfaces presque géodésiques à différents endroits», explique Kalegari.

Les travaux de Kahn et Markovich leur ont valu le Clay Institute of Mathematics Award 2012, décerné pour des percées mathématiques.

"Les techniques de Kahn et Markovich ne sont pas inférieures en termes d'intérêt à leurs résultats, et ce travail inspirera sans aucun doute de nombreux autres domaines de recherche qui s'y rapportent", a prédit Jeffrey Brock de l'Université Brown dans un article de 2011.

Structure cachée

Kan et Markovich ont créé le point de départ pour les mathématiciens essayant de prouver le VHC.

Ils ont montré que chaque collecteur est garanti pour contenir une surface incompressible. Mais cette surface peut passer à travers elle-même, peut-être en de nombreux endroits, et ne pas être encastrée. Afin d'obtenir le VGHYU sur la base des travaux de Kan et Markovich, les mathématiciens devaient trouver une couverture finie du collecteur, dans laquelle, exactement comme dans l'exemple avec des couleurs à six et trois pétales, la surface s'élève jusqu'à un ensemble de surfaces qui ne se coupent pas (bien qu'elles puissent se croiser). Si cela était possible, chacun d'eux serait une surface incompressible intégrée dans le revêtement, ce qui signifie que le revêtement serait Haken.

Mais comment trouver une telle couverture?

«Il y a un grand écart entre le travail de Kahn et Markovic et le WHC», explique Danfield. "Leur découverte était importante, mais il n'était pas clair si cela aiderait dans la recherche de surfaces intégrées."

Les travaux de Kahn et Markovich ont attiré l'attention de Daniel Wise de l'Université McGill. Wise a fait carrière dans la recherche sur la suppression des auto-intersections d'objets topologiques à l'aide de revêtements finis, mais il a travaillé dans le contexte des «complexes cubiques», des objets qui à première vue sont très différents des 3-variétés. Les travaux de Kahn et Markovich ont aidé Wise à montrer à d'autres mathématiciens que ces deux contextes ne sont pas si différents.

Le complexe cubique - c'est le complexe cubique (CC): c'est un ensemble de cubes, non seulement un cube tridimensionnel y est appelé «cube», mais aussi une forme dans un nombre quelconque de dimensions, composée de tous les points dont les coordonnées se situent, par exemple, sur les intervalles entre - 1 et +1. Par exemple, un carré est un cube à deux dimensions et un segment à une dimension. Les cubes du vaisseau spatial sont connectés les uns aux autres le long des coins, des bords, des faces et des côtés de dimensions supérieures.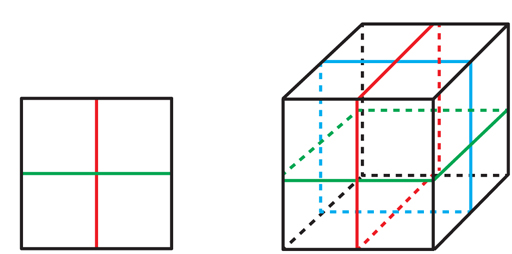

La figure 9

CC est très différente des variétés à 3 - ce ne sont même pas des variétés, car les intersections de deux cubes de dimensions différentes ne ressemblent à l'espace habituel d'aucune des dimensions. Mais les CC sont des objets simplifiés dans lesquels un aspect clé de la surface contenue dans les 3 variétés est étudié: le fait qu'une telle surface divise au moins localement son environnement en deux parties.

Si vous avez besoin d'explorer des objets qui divisent la forme en deux parties, les cubes sont le champ naturel pour commencer, en raison de toutes les formes possibles, ils ont le plus simple de ces objets: des hyperplans qui les coupent au milieu. Le carré a deux hyperplans (GP) - des lignes verticales et horizontales, le coupant en deux. Le cube a trois GPs (voir Fig. 9). Un cube à n dimensions a n GP se coupant en son centre.

«Les hyperplans s'apparentent à des surfaces dans 3 collecteurs, mais vous les voyez instantanément», explique Wise. «Il est difficile de rechercher des surfaces, mais les hyperplans sont à votre disposition dès le départ.»

Si nous commençons avec un GP à l'intérieur d'un cube dans un QC, alors il y a exactement une façon d'étendre un GP à un GP dans des cubes voisins; après cela, il y a exactement une façon de les étendre aux voisins; et ainsi de suite. Par conséquent, pour chaque GP initial dans le CC, il existe une façon unique de l'étendre au GP dans l'ensemble du CC (voir Fig. 10).

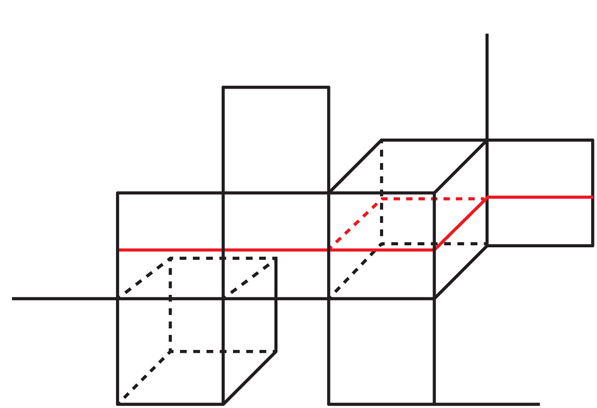Fig.10. L'hyperplan rouge dans le carré le plus à droite se développe de manière unique en un hyperplan dans l'ensemble du complexe cubique.

Cette qualité contraste fortement avec les 3 collecteurs, dans lesquels une petite surface peut être étendue à toute la surface de nombreuses manières. CC avec leurs généralistes est "beau, limpide et strict", dit Eigol, et ils n'ont pas la "flasque" des 3 collecteurs et de leurs surfaces.

Lorsque nous développons le GP dans le vaisseau spatial, il peut tomber sur le cube à partir duquel tout a commencé et le traverser perpendiculairement au GP initial (voir Fig.11). En d'autres termes, un GPU étendu ne sera pas nécessairement intégré. Comme c'est le cas avec les surfaces à l'intérieur de 3 variétés, on peut se demander si le QC a un revêtement fini dans lequel ces GPs auto-entrecroisés montent en GP intégrés - c'est la version de l'hypothèse virtuelle de Haken pour KK.

Fig.11

Il y a quelques années, Wise et Frédéric Haglund de l'Université Paris-Sud XI ont identifié une classe de QC «spéciaux» qui, en plus d'autres propriétés, n'ont que des GPU intégrés. Au cours de la dernière décennie, Wise a développé un arsenal de techniques adaptées pour identifier les «QC spéciaux». En 2009, Wise a publié un «travail principal» de 200 pages, comme Danfield l'a appelé, dans lequel il a décrit un ensemble de découvertes liées aux QC spécifiques, tels que les «théorèmes de combinaison», montrant comment assembler des QC spéciaux pour garantir de nouveaux QC, possédant également une «spécialité». Dans son travail, Wise a formulé une hypothèse qui énonçait, en gros, que tout CQ avec une géométrie se pliant d'une manière similaire à une géométrie hyperbolique est «virtuellement» spécial - c'est-à-dire qu'il a une couverture finie spéciale. Cette hypothèse a été appelée l'hypothèse Wise.

Wise était convaincu que si cette forme est en quelque sorte similaire à QC - quand elle peut être "cubée" - alors la structure QC sera la clé pour découvrir de nombreuses propriétés de la forme originale.

"CC était un secret que les gens ne savaient même pas quoi demander", a-t-il déclaré. "Il s'agit d'une structure cachée fondamentale."

Forêts cubiques

Weise était extrêmement préoccupé par le cubage des formes, mais au début, ses collègues se moquaient de lui à cause de cette manie.

Puis Kahn et Markovich ont prouvé le théorème des surfaces incompressibles, et Wise et Bergeron ont immédiatement publié un article montrant que l'existence de surfaces incompressibles dans un collecteur hyperbolique compact 3 donne une méthode pour le cuber - et de sorte que les surfaces du collecteur 3 correspondent exactement aux hyperplans dans le complexe cubique résultant .

La clé de la conception de Wise et Bergeron était le fait que Kahn et Markovich ont montré comment construire non pas une, mais plusieurs surfaces. Suivant l'approche du cubage, formulée pour la première fois en 2003 par Michael Sageev, qui travaille maintenant à Technion (Israël), Wise et Bergeron ont commencé par prendre une énorme collection de surfaces de Kahn-Markovich - assez pour diviser un manifold 3 en polygones compacts.

Imaginez maintenant l'un des points d'intersection de ces surfaces - par exemple, il y a n surfaces. La conjecture de Sageev était de considérer cette intersection comme une ombre, pour ainsi dire, à partir de l'intersection de n hyperplans dans un cube à n dimensions. Un KK correspondant à une variété 3 est construit, en gros, en ajoutant un cube à n dimensions pour chaque intersection de n surfaces (en réalité, tout cela est construit plus subtilement pour prendre en compte diverses circonstances topologiques imprévues). Deux cubes dans un complexe sont adjacents si leurs points d'intersection correspondants dans un collecteur à 3 sont connectés par la face de l'un des polytopes.

«Le complexe cubique est nécessaire pour calculer avec précision la façon dont les surfaces se croisent les unes avec les autres», explique Danfield.

Wise et Bergeron ont montré que ce KK est «homotopiquement équivalent» au collecteur d'origine, c'est-à-dire que le KK peut être compressé et étiré (en tenant compte de l'aplatissement dans certaines dimensions et du processus inverse) jusqu'à ce que le KK se transforme en collecteur, et vice versa. De plus, cette équivalence homotopique transforme chaque surface d'un 3-collecteur en GP homotopique correspondant en KK.

Le QC ainsi construit satisfait aux exigences géométriques de l'hypothèse Wise, ce qui signifie que si l'hypothèse Wise est vraie, alors ce QC a une couverture finie dans laquelle tous les GP seront intégrés.

Si un tel revêtement final existe vraiment (par exemple, couvrant m feuilles), alors nous devons nous rappeler que le revêtement peut être construit à partir du QC lui-même, en le découpant d'une manière spéciale, puis en faisant m copies de ce QC et en les collant ensemble le long des lignes de coupe. Il est facile de montrer que cette recette pour la fabrication d'un revêtement peut être transférée à la fabrication d'un revêtement final d'un 3-collecteur, et que dans ce revêtement final, les surfaces de Kan-Markovich utilisées pour construire le CC s'élèveront aux surfaces encastrées. En d'autres termes, si l'hypothèse de Wise est vraie, l'IHC l'est également.

«Il s'agit d'un compromis très étrange: votre QC peut être, par exemple, de 10 000 dimensions, et il peut vous sembler que, dans un certain sens, vous aggravez la situation», explique Wise. "Mais même en dépit de la valeur QC, bon nombre de ses propriétés sont très faciles à comprendre, donc cette procédure est très précieuse." "Nous préférons quelque chose de grand, mais bien organisé, au lieu de 3."

Même après que Wise et Bergeron ont établi une connexion entre QC et VGH, la plupart des topologues étudiant les 3 variétés sont restés à l'écart du QC. Peut-être parce que le travail de 200 pages de Wise était décourageant, ou parce que les CC étaient si différents de leurs espaces habituels.

«Ces idées étaient trop ésotériques pour les personnes issues de la géométrie hyperbolique», explique Bergeron.

Mais un mathématicien connaissait déjà bien la topologie des variétés 3, ainsi que les choses combinatoires plus abstraites que Wise a utilisées dans son approche.

«Je pense que Jan Eigol était le seul spécialiste des 3 variétés qui a compris assez tôt comment les idées de Wise pouvaient être utilisées pour la topologie des 3 variétés», explique Bergeron.

Eigol a approfondi l’étude du «travail principal» de Wise et s’est convaincu que toutes ses parties liées à l’hypothèse de Wise étaient correctes. Aigol est impliquée dans VHC depuis un certain temps; il a réalisé que l'approche de Wise, transformant des surfaces flasques en hyperplans cristallins, était exactement ce dont il avait besoin.

"KK nous donne des forêts pour la construction du revêtement final", a-t-il déclaré.

Pour construire un revêtement final spécial sur le vaisseau spatial Wise-Bergeron, Aigol a commencé à découper le vaisseau spatial le long du GP en «cubes Lego». Il a ensuite assigné des couleurs aux faces des blocs, de sorte que deux faces trouvées sur le coin aient des couleurs différentes. Ensuite, Eigol a montré qu'en gros, il existe un moyen de coller un nombre fini de copies de cubes Lego le long de visages de mêmes couleurs de telle sorte que les couleurs sur les côtés de ces visages correspondent également. Par conséquent, chaque GP étendu sera de la même couleur. Le QC résultant sera le revêtement final de l'original, et tous ses GPs seront intégrés, car deux GPs qui se croisent seront de couleurs différentes, donc ce ne sera pas un GP se croisant.

Le 12 mars, Aigol annonce la preuve de l'hypothèse Wise, et donc de l'hypothèse virtuelle Haken.

"C'était la nouvelle la plus excitante depuis que Perelman a prouvé l'hypothèse de la géométrisation", a déclaré Danfield.

L'information est passée par une communauté de chercheurs de 3 variétés, et le CQ est immédiatement devenu un sujet commun à tous les topologues.

"Je pense que jusqu'à présent, la communauté mathématique n'a pas compris à quel point le travail de Wise est puissant", a déclaré Aigol. «Je pense que mon résultat expliquera aux gens les progrès incroyables qu'il a réalisés.»

Maintenant, selon Wise, les mathématiciens commencent à réaliser que "chaque fois que vous placez quelque chose, vous pouvez révéler toutes sortes de secrets de la structure".

Fin d'une époque

La preuve d'Aigol de la théorie de Wise était une preuve de «4 pour le prix de 1»: elle prouva non seulement le VGH, mais aussi les trois autres des 23 questions de Thurston, qui jusque-là restaient ouvertes. Dans le temps menant à la preuve, Eigol et d'autres mathématiciens ont montré que ces trois questions - l'hypothèse du faisceau virtuel et deux autres questions techniques concernant les variétés 3 hyperboliques - découlaient également de l'hypothèse de Wise.

Dans le cas de l'hypothèse du faisceau virtuel, nous rappelons que le but était de montrer que chaque collecteur hyperbolique compact 3 a un revêtement fini qui est fibré en cercle, c'est-à-dire construit en collant les parties opposées d'une surface épaissie. Du VGH, nous savons qu'un collecteur a un revêtement Hakenov fini - c'est-à-dire que le revêtement a une surface incompressible intégrée. Si vous ouvrez le collecteur Haken le long de cette surface, vous obtiendrez quelque chose qui ressemble à une surface épaissie aux extrémités, mais comme Dieu sait ce qu'il y a dans les "tripes".

Yang Aigol lors d'un récent voyage à Daejeon, en Corée du Sud.

En 2008, selon Kalegari, il y a eu une «percée surprenante» quand Eigol a montré que les 3 variétés hyperboliques satisfaisant à des conditions techniques spéciales sont garanties d'être pratiquement stratifiées. L'année suivante, Wise a montré sur cette base que toutes les variétés de Haken sont pratiquement stratifiées. Autrement dit, il existe un moyen d'agrandir le collecteur de Haken pour obtenir une couverture finie qui révèle une topologie complexe et conduit à un collecteur feuilleté simple. Par conséquent, si le collecteur est pratiquement Hakenov, il doit être virtuellement stratifié.

"Je pense que tout le monde croyait que le VGH serait vrai, mais l'hypothèse du bundle virtuel nous semblait moins accessible", a déclaré Kalegari. "Pour moi, le fait que l'hypothèse de stratification virtuelle découle de la VGH est l'un des aspects les plus choquants de toute cette histoire."

Avec la preuve de l'hypothèse du bundle virtuel, "vous pouvez être tenté et décider que les variétés à 3 sont trop simples parce que les variétés stratifiées en cercle sont simples", a déclaré Minsky. "Mais je pense que cela nous enseigne que les variétés qui sont stratifiées en cercle ne sont pas du tout simples et plus rusées que ce à quoi nous nous attendions."

Dans le même temps, le théorème du faisceau virtuel signifie qu'il existe une recette simple et informative pour créer tous les 3 collecteurs hyperboliques compacts: commencez par une surface épaissie, collez ensemble ses bordures intérieure et extérieure avec des rotations à votre goût, et pliez le collecteur sur lui-même un nombre fini de fois.

«Si vous me demandiez un manifold hyperbolique 3, je vous demanderais de quel type vous avez besoin - quel type de paquet et de revêtement final? - dit Kalegari. "Maintenant, nous savons que dans ce processus, nous ne manquons pas un seul 3-collecteur."

Bien que les mathématiciens aient besoin de temps pour tester minutieusement le travail d'Eigol, beaucoup d'entre eux sont optimistes quant à la réussite du test.

«Jan Aigol n'est pas une personne négligente», explique Minsky.

Maintenant que, apparemment, la dernière question de la liste de Thurston a été résolue, les chercheurs commencent à se demander à quoi ressemblera la région topologique des 3 variétés dans un nouveau monde courageux après Thurston.

Les mathématiciens conviennent qu'ils auront beaucoup de travail à trouver des choses utiles que le CQ peut offrir pour les formes cubables. Et pour les 3 variétés elles-mêmes, selon Aigol, la fin de l'ère est venue - et le début de la suivante.

«Dans la plupart des domaines des mathématiques, aucun plan ne pourrait tracer la voie à suivre pour les 20 à 30 prochaines années, comme ce fut le cas avec nous», dit-il. Maintenant, suggère-t-il, la topologie des 3 variétés et la géométrie peuvent devenir similaires à d'autres domaines des mathématiques dans lesquels les scientifiques se touchent et progressent même sans le luxe d'une grande image hypothétique de ce qui se passe.

«Les nouvelles générations de mathématiciens poseront les questions importantes suivantes», explique Aigol.

On se met en forme: de la géométrie hyperbolique aux complexes cubiques et vice versa