En novembre 2012, Randal Monroe a publié une bande dessinée xkcd avec un calendrier dans lequel la taille des numéros de chaque mois était proportionnelle à la fréquence à laquelle ce numéro est mentionné dans les livres sous son propre nom (par exemple, «14 octobre») dans la base de données Google Ngrams depuis 2000. La plupart des grandes dates sont assez évidentes: 4 Juillet , Décembre 25 , le premier jour de chaque mois, le dernier jour de presque tous les mois, et Septembre 11 , laissant tout le monde derrière. Peu de jours paraissent beaucoup plus petits que les autres. Par exemple, le 29 février- un petit point. Mais si vous regardez attentivement, vous pouvez voir que le 11e jour de chaque mois est relativement petit. Une note est allée à la bande dessinée: «Dans tous les mois sauf septembre, le 11 est mentionné beaucoup moins souvent que le reste des dates. C'était jusqu'au 11 septembre [2001], et je ne sais pas pourquoi il en est ainsi. " J'ai fouillé dans les données, et je pense avoir compris pourquoi.

Au début, je me suis assuré que le 11 était différent des autres. Un mois peut aller jusqu'à 31 jours, et certains de ces jours seront certainement les plus petits de tous. Peut-être que le 11e numéro du calendrier n'est pas le plus petit, juste notre œil s'y accroche. J'ai donc comparé les données réelles et pas seulement étudié les bandes dessinées. La base de données Ngrams renvoie le nombre total de fois où une phrase est mentionnée pendant un an, normalisé par le nombre de livres publiés cette année-là.

J'ai choisi le montant de chaque jour de l'année (1er janvier, 2 janvier) et tracé les médianespar mois pour chaque jour du mois (1er janvier, 1er février, etc.) pour chaque année. Cela montre à quelle fréquence les 11e et 30 autres jours sont mentionnés dans l'année sélectionnée. La médiane vous permet de lisser les salves de jours comme le 4 juillet. La médiane ne paraîtra inhabituelle que si le numéro de série est très différent dans au moins 6 mois sur 12.

J'ai construit des médianes pour chaque numéro de série de 2000 à 2008. Voici un histogramme pour 31 médianes. Le premier chiffre se démarque de tous et 15 sont à peine visibles parmi les autres. Mais le résultat du 11e jour est le moins important (avec une valeur P <0,05), ce qui à première vue est difficile à expliquer.

Et cette lacune existe depuis longtemps. Le graphique suivant montre tous les numéros de série pour chacune des années de 1800 à 2008. Les données sont lissées sur 11 ans pour éliminer le bruit. Même au tout début, le 11e est bien inférieur au groupe principal. Son léger défaut persiste pendant plusieurs décennies, puis dans les années 1860 le 11ème dévie soudainement de sa position de dernier dans la série médiane. L'écart entre le 11e et les numéros de série ordinaires augmente fortement et, par conséquent, la valeur de la fréquence de ses références devient environ la moitié inférieure, ce qui se poursuit dans la première moitié du 20e siècle. Au second semestre, l'écart se réduit, mais ne disparaît pas jusqu'au bout.

Les lecteurs attentifs remarqueront une autre bizarrerie. Il y a 4 lignes de plus qui sont inférieures à ce qu'elles devraient être. De haut en bas, ce sont les 2e, 3e, 22e et 23e numéros. De 1800 à 1890, ils sont même inférieurs au 11. Mais depuis 1900, leur écart se rétrécit, tandis que l'écart depuis le 11 commence à s'élargir et disparaît complètement dans les années 1930. C'est aussi un sujet assez intéressant, que nous examinerons un peu plus tard.

Curiosités typographiques

En commençant l'étude, j'espérais trouver un tabou secret sur les événements du 11 ou une déviation typographique des règles de la presse. Hélas, la raison s'est avérée beaucoup plus terre à terre: le nombre 1 est très similaire à la majuscule I (i) ou minuscule l (L) dans la plupart des polices utilisées pour imprimer les livres. Et aussi 11 peut être confondu avec n. Les algorithmes de Google se trompent, reconnaissant 11 sur la page, et interprètent le numéro de série comme une sorte de mot.

Nous pouvons rechercher directement des expressions dénuées de sens comme ll mars ou juillet II ou mai II. 11 peut être confondu avec neuf combinaisons de I, l et i. Cinq d'entre eux se trouvent en effet dans la base de données, au moins pendant un mois: II-nd, Il-nd, ii-nd, li-nd et ll-th. De plus, il y avait des options avec un seul mauvais caractère, 1lth, 1ith et l1th. J'ai appelé ces erreurs xxth. Livres Googleeffectue des requêtes vers une base de données plus récente que Ngrams, mais des exemples de telles erreurs peuvent toujours être trouvés. Par exemple , Google reconnaît ce qui suit comme janvier II:

comme le 11 février :

mais mars li :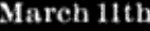

il y a beaucoup de tels exemples dans la base de données. Vous pouvez trouver d'autres numéros de série interprétés de manière erronée, mais le 11 est beaucoup plus courant que les autres.

J'ai ajouté le 2 janvier, le 11 janvier, etc. à mes calculs, et j'ai fait de même pour les autres mois. Le graphique suivant montre que le 11e reçoit un gros coup de pouce de cet ajout. Jusqu'aux années 1860, la différence entre le 11e et le groupe principal disparaît. Après les années 1860, un tiers ou un quart de cette différence a disparu.

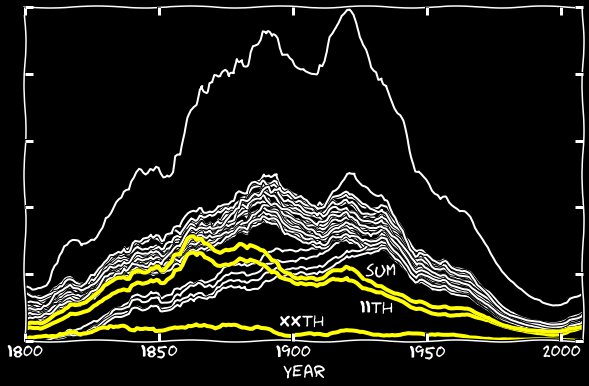Et où est passé le reste du 11? Depuis les années 1860, l'algorithme de Google commence à commettre une étrange erreur - au lieu du 11, il reconnaît les nèmes. Voici un exemple de page remplie des nièmes numéros de janvier:

Certaines années, le nombre de reconnaissances incorrectes dépasse le nombre de reconnaissances correctes. J'ai ajouté le nième jour de janvier au 11 janvier et j'ai fait de même avec les autres mois. Le graphique suivant montre les nièmes nombres et leur somme avec 11s. Jusqu'aux années 1860, leur contribution était négligeable, mais cette erreur commence à être responsable de presque tous les 11e manquants.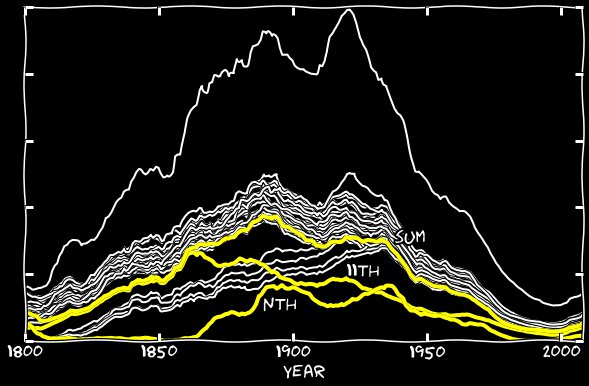

Horaire combiné

En ajoutant des xxième et nième erreurs au 11e graphique, j'ai comblé l'écart sur toute la longueur du graphique, et le 11e a commencé à ressembler à toutes les autres dates. Il s'avère que la reconnaissance incorrecte du 11 sous la forme du n, II, ll, etc., est responsable d'un petit nombre de 11 numéros entre autres jours du mois.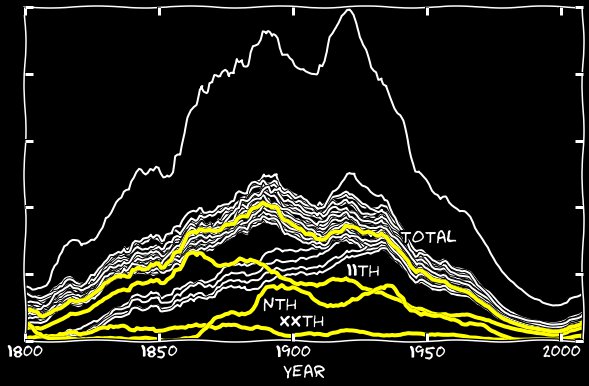

Machines à imprimer

Bien qu'il soit clair pourquoi le 11e a été plus souvent reconnu incorrectement que d'autres, pourquoi le nombre d'erreurs est-il si inégal? Que s'est-il passé dans les années 1860, à cause duquel le taux d'erreur a tellement bondi? Je soupçonne que cela est dû à l'invention dans les années 1860 d'un appareil tel qu'une machine à écrire. Les premières machines à écrire n'avaient pas de clé distincte pour le numéro 1 . Il a été proposé d'utiliser à la place la lettre l (L) en minuscules. Et lorsque l'algorithme reconnaît le 11 octobre, il le fait plus correctement que nous ne le pensions. Les livres Google n'ont pas beaucoup de documents dactylographiés, mais cet appareil populaire a eu un grand impact sur le développement des polices. 1 et l ne différaient pas sur des machines à écrire de plus en plus courantes, et même la police typographique commençait à répondre aux attentes de cette similitude. Comparez ces caractères dans une police1850 : La

différence entre l sans empattement en haut et 1 avec un empattement évident est visible. Comparez-les dans la police 1920 : les

caractères sont identiques à l'exception du crénage. Et aujourd'hui, la plupart des polices représentent 1 et l sous la forme de grands caractères avec deux empattements en dessous et un dirigé vers la gauche, au-dessus. Seul l'angle d'encoche 1 est légèrement supérieur à celui de l. La qualité d'impression des livres depuis 1970 a contribué à réduire le nombre de reconnaissances incorrectes, mais elles n'ont pas complètement disparu, de sorte que les problèmes restants sont apparus sur la bande dessinée de xkcd.

La question de la popularité de l'erreur reste ouverte, où 11 est remplacé par le nième. C'est une erreur assez étrange. Le nième se retrouve souvent dans les mathématiques et les publications scientifiques, ce qui peut affecter sa popularité. Dans la plupart des polices, la partie supérieure de n est très fine et peut ne pas être visible dans les textes sur lesquels l'algorithme a été formé. Mais il y a une grande différence dans la croissance de 1 et n, en particulier à l'ère des machines à écrire, où de nombreuses erreurs se produisent. Mais l'expression n-janvier est un non-sens, donc les chances d'une telle reconnaissance auraient dû être réduites. Peut-être que certains textes modernes contenaient des erreurs et que le 11e était marqué comme nième, ce qui a servi de source d'erreurs? La seule façon de le savoir est d'ouvrir le code source de l'algorithme de Google, qui reconnaît le texte. Nous laisserons cet exercice au lecteur.

Perdu 2, 3, 22 et 23

Nous avons compris les onzième nombres, mais pendant l'étude de leur comportement, je suis tombé sur un autre mystère - un nombre incompréhensiblement bas de 2, 3, 22 et 23 nombres, mais seulement jusqu'aux années 1930, après ce qui porte leur nombre égalisé.

Sur le graphique ci-dessous sont tous les nombres, et il s'avère que dans les années 1800, les dates indiquées ne sont pas du tout utilisées. Les premières références à nos dates sont apparues dans les années 1810, leur nombre augmente au même rythme que les autres dates, mais conserve en même temps un écart avec elles - leur nombre est environ deux fois moins élevé. Soudain, dans les années 1890, l'écart se rétrécit, et cela se produit jusqu'aux années 1930, quand ils fusionnent finalement dans le groupe principal.

Style pré-révolutionnaire

Alors, les numéros 2 et 3 du 19e siècle étaient-ils mécontents? L'algorithme de Google a-t-il à peine reconnu les deux et les triples dans les anciennes polices? Non, il s'avère que plus tôt au lieu du record anglais actuel «2nd, 3rd, 22nd, 23rd», il était habituel d'écrire «2d, 3d, 22d, 23d». J'ai construit une médiane pour le 2 janvier, le 2 février et d'autres mois, et j'ai fait de même avec les dates restantes. Le graphique ci-dessous montre la fréquence d'occurrence de ces dates dans l'ancien style d'enregistrement - elles commencent avec la fréquence d'autres dates, mais disparaissent progressivement dans les années 1890 et se dissolvent complètement dans les années 1930.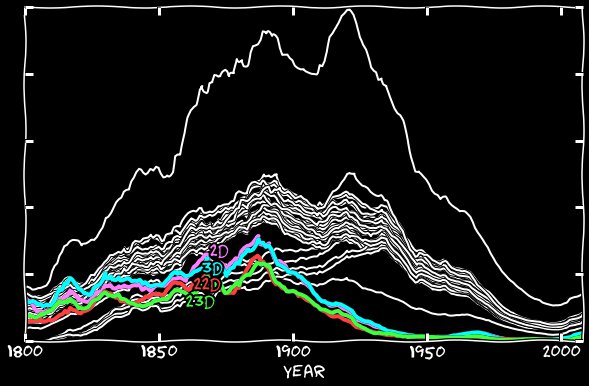

Parfois, vous pouvez trouver l'utilisation moderne de l'ancienne forme d'enregistrement, si elle est utilisée dans un titre avec une longue histoire, comme 3d Marine Division. Mais l'utilisation résiduelle d'un tel document est principalement due à l'existence de réimpressions de vieux livres et de publications de vieux journaux.

Horaire combiné

Si nous ajoutons l'ancien style au nouveau, nous obtenons le graphique suivant. Il s'ensuit que les dates correctement calculées ne sont presque pas différentes de toutes les autres.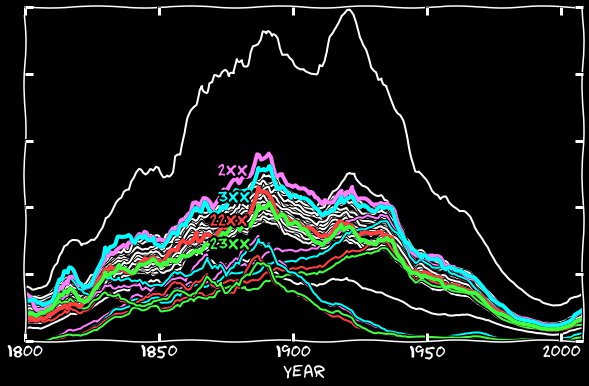

Pourquoi maintenant il s'avère que les références aux nombres 2 et 3 dépassent parfois les autres en fréquence, cela me reste incompréhensible. Je pense qu'en raison de la mention trop fréquente du 1er du mois, les 2e et 3e de la journée devraient également être mentionnés un peu plus souvent. Mais si vous regardez les événements du 2 janvier ou du 2 janvier dans Google Livres, vous pouvez trouver pas mal de ces passages:

Apparemment, Google Livres ignore les virgules. Ainsi, bien que les dates du mois de 1 à 4 n'aient rien de spécial, de tels exemples ici peuvent affecter les statistiques.

Raisonnement

Pourquoi les écrivains utilisaient-ils auparavant de telles abréviations à une seule lettre? Peut-être à cause du latin, où la lettre o servait d'indicateur du numéro de série. Les langues romanes telles que l'espagnol, l'italien et le portugais utilisent toujours o ou a. Nous utiliserions toujours d sinon pour 1er, 4e, etc., pour lesquels la dernière consonne n'est pas exprimée en anglais avec une lettre. Il s'est avéré que suivre la langue anglaise l'emportait sur le désir d'imiter le latin.

Manquant le onzième du mois et autres dates