Les informaticiens ont développé un algorithme de tarte équitable pour n'importe quel nombre de personnes

Deux jeunes scientifiques, experts dans le domaine de l'informatique, ont trouvé comment partager honnêtement un gâteau entre un nombre illimité de personnes, résolvant le problème que les mathématiciens luttent depuis des décennies. Leurs travaux ont surpris de nombreux chercheurs qui considéraient une telle séparation impossible en principe.

Partager une tarte est une métaphore pour un large éventail de tâches de la vie réelle, y compris la division d'un certain objet continu, qu'il s'agisse d'un gâteau ou d'un morceau de terre, entre des personnes qui valorisent ses propriétés différemment. L'un aime un enrobage au chocolat, l'autre veut des fleurs crème. Depuis les temps bibliques, un algorithme est connu pour diviser un tel objet entre deux personnes, de sorte que personne n'envierait l'autre: une personne divise le gâteau en deux parties égales pour lui, et l'autre choisit l'une d'entre elles. Dans la Genèse, Abraham (alors connu sous le nom d'Abram) et Lot ont utilisé cette méthode pour diviser le pays, quand Abraham est venu avec une séparation, et Lot a choisi entre le Jourdain et Canaan.

1960- « » . , 1995 [Steven Brams] - [Alan Taylor] -. «» , – «», , , .

- , « , -, », [Ariel Procaccia], informaticien à l'Université Carnegie Mellon, l'un des créateurs de Spliddit , un outil en ligne gratuit pour un partage équitable des tâches, des tâches ménagères aux frais de location partagés.

Au cours des 50 dernières années, de nombreux mathématiciens et informaticiens, dont Procaccia, se sont convaincus qu'il n'existe pas d'algorithme équitable limité pour diviser un gâteau en n parties.

«C'est cette tâche qui m'a conduit dans le domaine des divisions équitables», explique Walter Stromkvist[Walter Stromquist], professeur de mathématiques au Brin Mavre College en Pennsylvanie, qui a obtenu de bons résultats dans le problème du partage de gâteaux en 1980. "Toute ma vie, j'ai pensé que je retournerais à cette tâche pendant mon temps libre et prouver qu'une telle extension du résultat est en principe impossible" .

Mais, en avril, deux spécialistes de l'informatique ont réfuté ces attentes en publiant un algorithme de partage équitable du gâteau avec la durée de fonctionnement en fonction du nombre de participants au partage, et non de leurs préférences personnelles. Un scientifique, Simon Mackenzie , 27 ans , Ph.D., de Carnegie Mellon, a présenté son travail le 10 octobre lors de la 57e conférence annuelle de l'IEEE sur les bases de l'informatique.

L'algorithme est extrêmement complexe. Une partition de gâteau entre n participants peut nécessiter jusqu'à n^{n n n n n} étapes, avec approximativement le même nombre de coupes. Même pour un petit nombre de participants, ce nombre dépasse le nombre d'atomes dans l'univers. Mais les chercheurs ont déjà des idées pour simplifier et accélérer l'algorithme, selon un deuxième membre de l'équipe, Haris Aziz , un spécialiste en informatique de 35 ans de l'Université de Nouvelle-Galles du Sud, qui travaille dans le groupe de recherche australien Data61.

Les experts qui étudient la théorie de la division équitable , selon Procaccia, considèrent cela "certainement le meilleur résultat depuis des décennies".

Morceaux de gâteau

L'algorithme Aziz et Mackenzie est basé sur une procédure élégante inventée indépendamment par les mathématiciens John Selfridge et John Conway dans les années 1960, qui vous permet de diviser équitablement un gâteau en trois.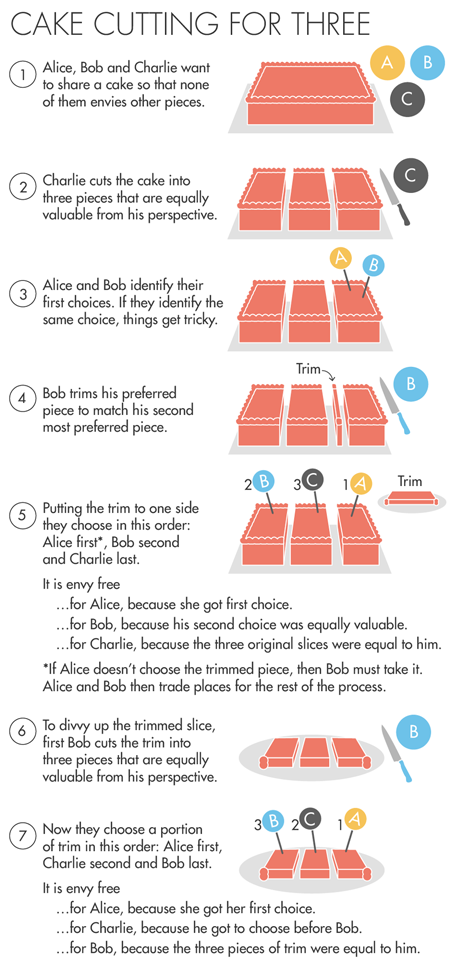



Si Alice, Bob et Charlie (A, B, C) veulent diviser le gâteau, l'algorithme commence avec Charlie divisant le gâteau en trois morceaux qui lui ressemblent. Alice et Bob choisissent les pièces qu'ils aiment. S'ils choisissent des pièces différentes - le tour est joué, chacun obtient ce qu'il veut.

Si Alice et Bob choisissent un morceau, alors Bob coupe une petite partie de ce morceau pour que le morceau devienne équivalent, de son point de vue, à un autre morceau de gâteau - celui que Bob choisirait en deuxième lieu. Le résidu coupé est reporté. Maintenant, Alice doit choisir la meilleure pièce pour elle-même parmi les trois autres, puis sélectionne Bob - à condition qu'il prenne la pièce coupée par lui, si Alice ne la sélectionne pas. Charlie obtient le troisième morceau.

En conséquence, personne n'envie personne. Alice a choisi le premier. Bob a reçu l'une des deux pièces de valeur égale pour lui. Charlie a obtenu l'une des trois pièces originales qu'il a lui-même découpées.

Il ne reste qu'une petite coupure. Mais il peut être divisé sans démarrer d'abord l'algorithme et sans tomber dans un cycle sans fin de circoncisions et de choix, car Charlie est en tout cas satisfait de sa pièce - et même si celui qui a obtenu la pièce coupée aurait reçu tout le reste en annexe, par exemple pour Charlie ne serait pas malhonnête, car le morceau coupé et le reste donneront un morceau de gâteau équivalent à son morceau - après tout, il a coupé ces morceaux dès le début. Aziz et Mackenzie décrivent la position de Charlie comme «dominante».

Maintenant, si, par exemple, Alice a obtenu la pièce coupée, puis Bob coupe la garniture en trois parties, équivalente de son point de vue, Alice sélectionne l'une de ces pièces pour elle-même, puis sélectionne Charlie, puis Bob. Tout le monde est heureux: Alice a choisi en premier, Charlie obtient un morceau mieux que Bob (et il ne se soucie pas de la quantité d'Alice), et du point de vue de Bob, les trois pièces sont équivalentes.

Brahms et Taylor ont utilisé la propriété de «dominance» (mais avec un nom différent) pour développer leur algorithme de 1995, mais ils n'ont pas terminé leur idée jusqu'à ce qu'un algorithme limité apparaisse. Au cours des 20 prochaines années, personne n'a obtenu les meilleurs résultats. «Et pas à cause du manque de tentatives», explique Procaccia.

Diviseurs de gâteau non professionnels

Lorsque Aziz et Mackenzie (A&M) ont décidé d'assumer cette tâche il y a quelques années, ils étaient nouveaux dans la tâche de partage de gâteaux. "Nous n'avions pas autant d'expérience que les personnes qui y ont travaillé intensivement", a expliqué Aziz. "Bien que ce soit généralement un inconvénient, dans notre cas, c'était un avantage, car nous pensions différemment."

A&M a commencé par étudier la tâche de diviser en trois participants à partir de zéro, et à la suite de l'analyse est venu à un algorithme équitable limité pour quatre participants , publié par eux l'année dernière.

Ils n'ont pas été en mesure de montrer immédiatement comment étendre leur algorithme à un nombre de participants supérieur à quatre, mais ils ont accepté cette tâche avec enthousiasme. «Après avoir envoyé le travail concernant quatre participants, nous voulions vraiment continuer rapidement le travail jusqu'à ce que quelqu'un de plus expérimenté et intelligent le généralise indépendamment au cas de n participants», explique Aziz. Et après environ un an, leur recherche a réussi.

Comme l'algorithme Selfridge-Conway, le protocole AiM propose constamment différents participants pour couper le gâteau en n parties égales, et d'autres pour couper et choisir des morceaux de gâteau. Mais il y a d'autres étapes dans l'algorithme, par exemple, l'échange périodique de morceaux de gâteaux d'une manière spéciale, afin d'augmenter le nombre de relations dominantes entre les participants.

Ces relations permettent à A&M de réduire la complexité de la tâche. Si, par exemple, trois participants dominent le reste, ils peuvent déjà être envoyés pour manger leurs propres morceaux de gâteau - ils seront heureux peu importe qui recevra les restes. Après cela, il reste moins de participants, et après un nombre limité de telles étapes, tout le monde est satisfait et le gâteau entier est divisé.

«En repensant à la complexité de l'algorithme, il n'est pas surprenant qu'il ait fallu si longtemps pour le développer», explique Procaccia. Mais les A&M croient déjà qu'ils peuvent simplifier l'algorithme afin qu'il ne nécessite pas d'échange de pièces et se déroule en seulement n ^{n n} étapes. Selon Aziz, ils travaillent déjà sur ces résultats.

Brahms prévient que même un algorithme plus simple n'aura pas d'application pratique - après tout, les morceaux de gâteau reçus par les participants comprendront de nombreuses petites miettes de différentes parties du gâteau. Cette approche n'est pas particulièrement utile si, par exemple, vous divisez le terrain.

Mais pour les mathématiciens et les informaticiens qui étudient le problème, le nouveau résultat «réinitialise tout le sujet», explique Stromquist.

Maintenant que les chercheurs savent que le gâteau peut être divisé en un nombre limité d'étapes, la prochaine étape, selon Procaccia, est de comprendre le grand écart entre la limite supérieure du nombre d'étapes par la méthode AiM et la limite inférieure du nombre d'étapes nécessaires pour cela. Procaccia a déjà prouvé plus tôt que l'algorithme de séparation équitable du gâteau ne peut pas passer en moins de n² étapes - mais le nombre d'étapes est minime par rapport à n ^{n n n n n} et même n ^{n n} .

Aziz dit que les chercheurs doivent maintenant trouver comment réduire cet écart. «Je pense que des progrès peuvent être réalisés dans les deux sens.»