La beauté des nombres. Constantes mathématiques dans la nature

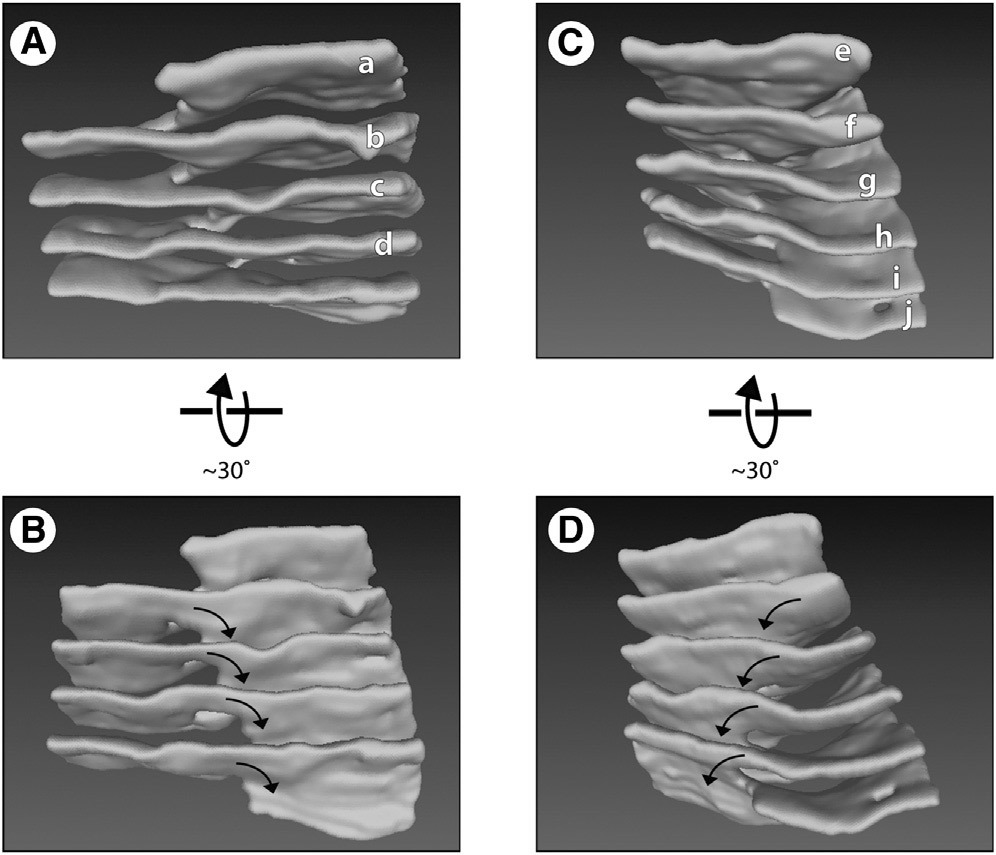Un modèle 3D du réticulum endoplasmique d'une cellule eucaryote avec des rampes Terasaki qui relient les feuilles plates de la membrane

En 2013, un groupe de biologistes moléculaires des États-Unis a étudié une forme très intéressante du réticulum endoplasmique - l'organoïde à l'intérieur de la cellule eucaryote. La membrane de cet organoïde est constituée de feuilles planes reliées par des "rampes" en spirale, comme si elles étaient calculées dans un programme de modélisation 3D. Ce sont les soi-disant rampes Terasaki. Trois ans plus tard, le travail des biologistes est remarqué par les astrophysiciens. Ils ont été étonnés: après tout, précisément de telles structures sont présentes à l'intérieur des étoiles à neutrons. La soi-disant "pâte nucléaire" est constituée de feuilles parallèles reliées par des formes en spirale.

L'incroyable similitude structurelle des cellules vivantes et des étoiles à neutrons - d'où vient-elle? De toute évidence, il n'y a pas de lien direct entre les cellules vivantes et les étoiles à neutrons. Juste une coïncidence?


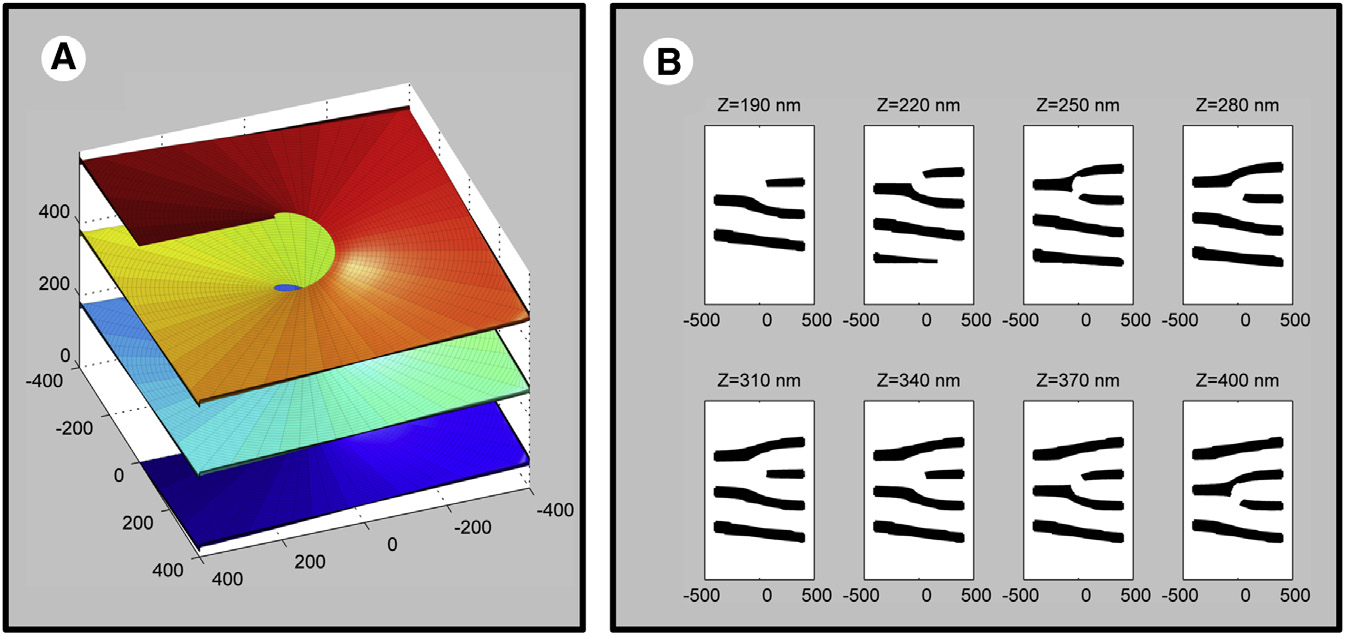Modèle de connexions en spirale entre des feuilles de membrane plates dans une cellule eucaryote

On suppose que les lois de la nature agissent sur tous les objets du micro et du macrocosme de telle sorte que certaines des formes et des configurations les plus optimales apparaissent comme si elles-mêmes. En d'autres termes, les objets du monde physique obéissent aux lois mathématiques cachées qui sous-tendent l'univers entier.

Regardons quelques autres exemples qui soutiennent cette théorie. Ce sont des exemples où des objets matériels essentiellement différents présentent des propriétés similaires.

Par exemple, les trous noirs acoustiques, observés pour la première fois en 2011, présentent les mêmes propriétés que les vrais trous noirs devraient avoir en théorie. Dans le premier trou noir acoustique expérimentalLe condensat de Bose-Einstein de 100 000 atomes de rubidium n'a pas été tordu à une vitesse supersonique de telle manière que certaines parties du condensat ont traversé la barrière acoustique, contrairement aux voisins. La limite de ces parties de condensat simulait un horizon d'événement de trou noir, où la vitesse d'écoulement est exactement égale à la vitesse du son. À des températures proches du zéro absolu, le son commence à se comporter comme des particules quantiques - phonons(une quasi-particule fictive représente un quantum du mouvement vibratoire des atomes de cristal). Il s'est avéré qu'un trou noir «sonore» absorbe les particules de la même manière qu'un vrai trou noir absorbe les photons. Ainsi, le flux de fluide agit sur le son de la même manière qu'un véritable trou noir agit sur la lumière. En principe, un trou noir sonore avec des phonons peut être considéré comme un modèle particulier de courbure vraie dans l'espace-temps.

Si vous regardez plus largement les similitudes structurelles dans divers phénomènes physiques, vous pouvez voir un ordre incroyable dans le chaos naturel. Tous les divers phénomènes naturels sont, en fait, décrits par de simples règles de base. Règles mathématiques.

Prenez les fractales. Ce sont des formes géométriques auto-similaires qui peuvent être divisées en parties de sorte que chaque partie soit au moins approximativement une copie réduite de l'ensemble. Un exemple est la célèbre fougère Barnsley.



La fougère de Barnsley est construite en utilisant quatre transformations affines de la forme:



Cette feuille particulière est générée avec les coefficients suivants: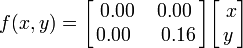









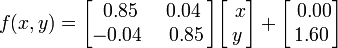
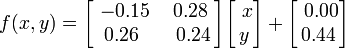Dans notre environnement, de telles formules mathématiques se trouvent partout - dans les nuages, les arbres, les chaînes de montagnes, les cristaux de glace, les flammes vacillantes, sur la côte de la mer. Ce sont des exemples de fractales dont la structure est décrite par des calculs mathématiques relativement simples.

Galileo Galilei en 1623 a déclaré: «Toute la science est écrite dans ce grand livre - je veux dire l'Univers - qui nous est toujours ouvert, mais qui ne peut pas être compris sans apprendre à comprendre la langue dans laquelle il est écrit. Et il est écrit dans le langage des mathématiques, et ses lettres sont des triangles, des cercles et d'autres figures géométriques, sans lesquelles il est impossible pour une personne de distinguer ses mots; sans eux, il est comme errant dans les ténèbres. »

En fait, les règles mathématiques se manifestent non seulement dans la géométrie et les contours visuels des objets naturels, mais aussi dans d'autres lois. Par exemple, dans la dynamique non linéaire de la population, dont le taux de croissance diminue dynamiquement à l'approche de la limite naturelle de la niche écologique. Ou en physique quantique.

Quant aux constantes mathématiques les plus connues - par exemple, le nombre pi - il est tout à fait naturel qu'elle se retrouve largement dans la nature, car les formes géométriques correspondantes sont les plus rationnelles et adaptées à de nombreux objets naturels. En particulier, le nombre 2π est devenu la constante physique fondamentale. Il montre quel est l'angle de rotation en radians, qui est contenu dans une révolution complète lorsque le corps tourne. En conséquence, cette constante se retrouve partout dans la description de la forme rotationnelle du mouvement et de l'angle de rotation, ainsi que dans l'interprétation mathématique des oscillations et des ondes.

Par exemple, la période de petites vibrations naturelles d'un pendule mathématique de longueur L immobile suspendu dans un champ gravitationnel uniforme avec une accélération gravitationnelle g est



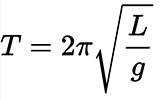Dans des conditions de rotation de la Terre, le plan d'oscillation du pendule tournera lentement dans le sens opposé au sens de rotation de la Terre. La vitesse de rotation du plan d'oscillation du pendule dépend de sa latitude géographique .



Le nombre pi fait partie intégrante de la constante de Dirac - la constante de Planck réduite, la principale constante de la physique quantique, qui relie deux systèmes d'unités - quantique et traditionnel. Il relie l'amplitude du quantum d'énergie de tout système physique oscillatoire linéaire avec sa fréquence.



En conséquence, le nombre pi est inclus dans le postulat fondamental de la mécanique quantique - le principe d'incertitude de Heisenberg.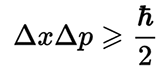



Le nombre pi est utilisé dans la formule constante de structure fine- une autre constante physique fondamentale caractérisant la force de l'interaction électromagnétique, ainsi que dans les formules hydromécaniques, etc.

Dans le monde naturel, vous pouvez trouver d'autres constantes mathématiques. Par exemple, le nombre e , la base du logarithme naturel. Cette constante est incluse dans la formule de la distribution de probabilité normale, qui est donnée par la fonction de densité de probabilité: La



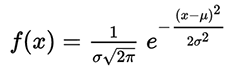distribution normale est soumise à de nombreux phénomènes naturels, y compris de nombreuses caractéristiques des organismes vivants dans une population. Par exemple, la distribution de taille des organismes dans une population: longueur, hauteur, superficie, poids, tension artérielle chez l'homme et bien plus encore.

Une observation attentive du monde qui nous entoure montre que les mathématiques ne sont pas du tout une science abstraite sèche, comme cela peut sembler à première vue. Bien au contraire. Les mathématiques sont le fondement de tout le monde vivant et non vivant qui l'entoure. Comme Galileo Galilei l'a correctement noté, les mathématiques sont le langage que la nature nous parle.

Source: https://habr.com/ru/post/fr398987/