Calculatrice de carton et de balle à quatre bits
Apparition d'une calculatrice en carton à quatre bits en carton. Le demi-additionneur en haut et les trois additionneurs au milieu et en bas de la calculatrice sont clairement visibles.Il était une fois, avant l'invention de l'électronique, les gens fabriquaient des ordinateurs mécaniques à partir de matériaux improvisés. L'exemple le plus célèbre et le plus complexe d'une telle machine est le mécanisme anticythère - un appareil complexe d'au moins 30 vitesses a été utilisé pour calculer le mouvement des corps célestes et a permis de connaître la date de 42 événements astronomiques.De nos jours, les ordinateurs mécaniques (calculatrices) sont plus probablement un objet de divertissement pour les geeks et une occasion d'organiser un spectacle amusant. Par exemple, comme un ordinateur de 10 000 tuiles domino qui additionne des nombres binaires à quatre chiffres arbitraires et produit une somme à deux chiffres à cinq chiffres (théorie mathématique de cette calculatrice et architecture ). De telles performances permettent aux enfants de mieux comprendre comment les opérations de logique binaire dans la programmation fonctionnent et comment les portes logiques sont organisées. Et en général, il est très intéressant de fabriquer un petit ordinateur avec ses propres mains à partir de matériaux improvisés, surtout si vous le faites avec votre enfant.
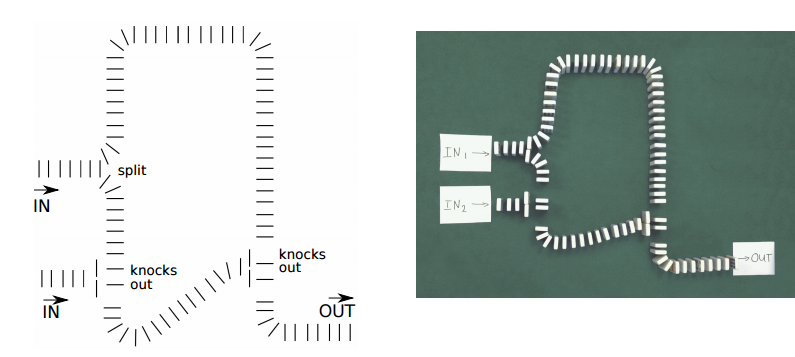L'opération logique ET dans un ordinateur de 10 000 tuiles dominoPour la fabrication d'une calculatrice mécanique, le constructeur Lego est excellent. Vous pouvez trouver de nombreux exemples de ces calculatrices sur YouTube .Calculatrice informatique LEGOInspiré par l'exemple d'un ordinateur composé de dominos et de calculatrices mécaniques du constructeur Lego, le programmeur C ++ sous le surnom lapinozz, avec ses sœurs cadettes, a décidé de construire à la maison quelque chose de similaire pour l'un des projets scientifiques de l'école de la sœur. Il a conçu et implémenté une calculatrice LOGIC quatre bits entièrement fonctionnelle (Logic cardbOard Gates Inpredictable Calculator) . Pour produire cet ordinateur, rien n'est nécessaire sauf le carton et la colle, et il ne fonctionne pas sur l'électricité, mais sur les billes et la gravité terrestre. La calculatrice peut ajouter des nombres de 0 à 15 avec un maximum de 30.Contrairement aux carreaux domino Lego et aux briques Lego, aucun composant d'usine n'a été utilisé dans la fabrication de cette calculatrice. Tous les éléments de la calculatrice sont collés à partir de carton à partir de zéro, ce qui est bien compris sur les photos de l'appareil. En ce sens, cet appareil peut être considéré comme unique.But du projet
Représentation visuelle de la façon d'ajouter des nombres binaires. Apprendre à un élève à traduire de la décimale en binaire et inversement. Étude des opérations de logique binaire et des circuits logiques de base.Apparence de la calculatrice
Comme vous pouvez le voir sur la photo de la calculatrice, dans la partie supérieure il y a une zone pour entrer des données. Après avoir terminé toutes les opérations logiques, les boules montrent le résultat de l'opération ci-dessous.
La saisie des données s'effectue par balles. La balle est - 1, la balle n'est pas - 0. Le bit de droite est le plus petit bit du nombre. Avant de commencer le travail, certaines parties de la calculatrice doivent être ramenées à leur position d'origine. Après avoir spécifié les valeurs initiales, la bande de carton est repoussée, ce qui maintient les boules dans la position initiale - et le processus d'addition commence.Par exemple, il s'agit de la position initiale des billes pour l'opération 7 + 5 (0111 + 0101).
Dispositif de calculatrice
Les opérations logiques d'une calculatrice en carton sont effectuées d'une manière similaire, comme dans l' ordinateur domino susmentionné .Les portes logiques schématiques pour toutes les opérations logiques sont illustrées dans le diagramme.
C'est-à-dire que la porte logique "ET" (ET) signifie que lorsque 0 billes sont reçues à l'entrée, 0 à la sortie est obtenue. Lors de la réception d'une balle à l'entrée, 0 est obtenu à la sortie. A réception de 2 balles à l'entrée, 1 à la sortie est obtenue.1 en entrée, 0 en sortie
2 en entrée, 1 en sortie
La porte logique XOR est un peu plus compliquée. Dans ce cas, si une balle arrive, elle doit passer. Et si deux boules arrivent, alors elles doivent s'annuler, c'est-à-dire que la sortie sera 0. L'auteur montre comment faire, à travers un morceau de carton suspendu verticalement avec un col étroit. Si deux boules arrivent en même temps, alors elles se bloquent - et mettent ainsi en œuvre efficacement l'opération logique XOR.Porte logique XOR
Afin d'optimiser le système et de ne pas bloquer la masse des portes logiques ET et XOR, l'auteur a implémenté un demi-additionneur- un circuit logique combinatoire à deux entrées et deux sorties. Le demi-additionneur vous permet de calculer la somme de A + B, avec pour résultat deux bits S et C, où S est le bit de la somme modulo 2 et C est le bit de retenue. Dans notre construction en carton, cela signifie que si nous avons 1 balle à l'entrée, alors elle va à la sortie C, et s'il y a 2 balles à l'entrée, alors 1 balle va à la sortie S, et la seconde ne va nulle part.Le programmeur a proposé un schéma assez simple et efficace pour un demi-additionneur. Dans celui-ci, 1 balle à l'entrée continue calmement son chemin, tournant la barrière et passant dans le trou C.Mais si deux balles entrent, alors la deuxième balle ne peut plus passer à travers la barrière, retournée par la première balle - et tombe dans le trou, clouant un nouveau chemin S. Ceci est un demi-additionneur.Une balle à l'entrée du demi-additionneur
Deux boules à l'entrée du demi-additionneur
Enfin, l'additionneur est un véritable chef-d'œuvre. Habituellement, il est composé de deux demi-additionneurs et d'une porte logique «OU», mais l'auteur a mis en œuvre une autre conception, qui est en fait une petite modification du demi-additionneur.Une balle à l'entrée - une balle sur le chemin 1
Deux balles à l'entrée - une balle sur le chemin 2
Trois balles à l'entrée - une balle sur le chemin 1 et l'autre le long du chemin 2
L'ensemble de la calculatrice est entièrement composé d'un demi-additionneur et de trois additionneurs.
La calculatrice donne le résultat de calcul correct si les balles tombent à la bonne vitesse, ni trop vite ni trop lentement, et ne rebondissent pas entre elles. La logique elle-même est sans faille, mais en pratique, la calculatrice est parfois boguée.Source: https://habr.com/ru/post/fr399391/
All Articles