Des structures mystérieuses combinent mathématiques et nature

Dans la ville de Cuernavaca au Mexique, un réseau "espion" augmente l'efficacité du parc de bus. Par conséquent, l'horaire de départ des bus correspond toujours au modèle «d'universalité»

En 1999, alors qu'il était assis à un arrêt de bus à Cuernavaca, au Mexique, le physicien tchèque Petr Šeba a remarqué que des gens donnaient des morceaux de papier aux chauffeurs de bus en échange d'argent. Il a constaté que ce n'était pas une manifestation du crime organisé, mais un commerce «fantôme» différent: chaque conducteur a payé un «espion», notant quand le bus précédent avait quitté l'arrêt de bus. S'il est parti récemment, le conducteur de ce bus a ralenti afin que les passagers puissent se rassembler au prochain arrêt. Si ce bus est parti il ​​y a longtemps, le conducteur a accéléré pour que les autres bus ne le dépassent pas. Un tel système maximise les profits des conducteurs. Ce qui a donné une idée à Sheba.

«Nous pensions que nous observions une situation qui rappelle quelque peu les systèmes quantiques chaotiques», a expliqué le co-auteur de Sheba, Milan Krbálek.

Après plusieurs tentatives infructueuses de communiquer avec les «espions», Sheba a demandé à son élève d'expliquer qu'il n'était ni de la taxe ni de la mafia. Il est juste un savant fou qui change la tequila pour leurs données. Et les gens lui ont donné leurs notes. Lorsque les chercheurs ont tracé des milliers d'heures de départ des bus, leurs soupçons ont été confirmés. L'interaction entre les conducteurs a conduit à la répartition des écarts entre les déchets de transport, qui a coïncidé avec la structure de certaines expériences en physique quantique.

"Je pensais que quelque chose comme ça pourrait apparaître, mais j'ai été surpris de voir une telle coïncidence exacte", a déclaré Sheba.

Les particules subatomiques ont peu en commun avec un système de bus décentralisé. Mais au fil des années depuis la découverte d'étranges interactions quantiques, les mêmes structures de données sont apparues dans d'autres situations sans rapport. Les scientifiques pensent que ce phénomène commun, connu sous le nom d '"universalité", est dû à la connexion mathématique des phénomènes, et les aide à simuler des systèmes complexes, de l'Internet au climat de la planète.


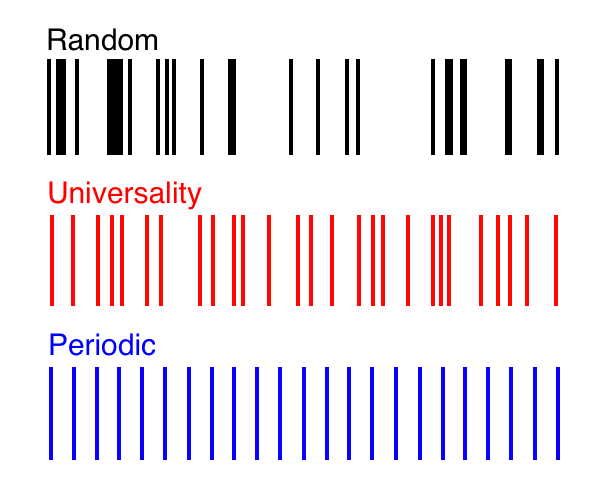Le graphique rouge représente l'équilibre parfait entre le caractère aléatoire et la périodicité, connu sous le nom d'universalité. Il est observé dans les spectres de nombreux systèmes complexes avec corrélation. Dans ce spectre, la fonction de corrélation mathématique donne la probabilité exacte de la présence de deux raies à une distance donnée l'une de l'autre.

Une telle structure a été trouvée pour la première fois dans la nature dans les années 50 dansspectre d'énergie d'un noyau d'uranium , un monstre avec des centaines de pièces mobiles, oscillant et s'étirant d'un nombre infini de façons, et donnant une séquence infinie de niveaux d'énergie. En 1972, Hugh Montgomery, spécialiste de la théorie des nombres, l'a observé aux zéros de la fonction zêta de Riemann , un objet mathématique lié à la distribution des nombres premiers. En 2000, Krbalek et Sheba l'ont trouvée sur un horaire de départ de bus à Cuernavaca . Et récemment, il est apparu dans les mesures spectrales de matériaux composites, tels que la glace de mer et le tissu osseux humain, et dans la dynamique des signaux du modèle Erd -s-Reni , une version simplifiée d'Internet.

Chacun de ces systèmes a un spectre - une séquence de codes à barres représentant des données telles que les niveaux d'énergie, les zêta zéros, les heures de départ des bus ou les vitesses des signaux. Des structures identiques apparaissent dans tout le spectre. La distribution des données semble aléatoire, mais en même temps, les lignes adjacentes se «repoussent», ce qui conduit à une certaine régularité des écarts. L'équilibre exact entre le chaos et l'ordre, déterminé par la formule, apparaît également dans des problèmes purement mathématiques: il détermine la distance entre les valeurs propres d'une matrice remplie de nombres aléatoires.

«Pourquoi tant de systèmes physiques se comportent comme des matrices aléatoires reste un mystère», explique Horng Tzer Yao, mathématicien à l'Université de Harvard. "Mais au cours des trois dernières années, nous avons franchi une étape très importante pour comprendre cela."

Pour étudier le phénomène d'universalité dans des matrices aléatoires, les scientifiques comprennent un peu pourquoi il apparaît partout et comment il peut être utilisé. Dans une pile de nouveaux articles, Yao et d'autres mathématiciens ont décrit de nombreux nouveaux types de matrices aléatoires qui obéissent à plusieurs distributions numériques et règles de symétrie. Par exemple, les nombres des colonnes et des lignes de matrices peuvent être tirés de la courbe de distribution normale des valeurs possibles, ou vous pouvez la remplir avec les valeurs 1 et -1. Les parties supérieure droite et inférieure gauche de la matrice peuvent se refléter ou ne pas s'afficher. Et quelles que soient leurs caractéristiques, les matrices aléatoires présentent les mêmes spectres chaotiques mais réguliers dans la distribution de leurs valeurs propres. Par conséquent, les mathématiciens ont appelé ce phénomène «universalité».

"Cela ressemble à une loi de la nature", a déclaré Wang Wu, mathématicien à l'Université de Yale, qui, avec Terence Tao de l'Université de Californie à Los Angeles, a prouvé l'universalité pour une large classe de matrices aléatoires.

On pense que l'universalité apparaît dans des systèmes très complexes, composés de nombreuses parties qui interagissent étroitement les unes avec les autres pour créer un spectre. Une configuration apparaît dans le spectre d'une matrice aléatoire, par exemple, car tous les éléments de la matrice sont utilisés dans le calcul de ce spectre. Mais selon Wu, les matrices aléatoires ne sont que des «systèmes de jouets», elles sont suffisamment simples à apprendre et suffisamment riches pour modéliser des systèmes réels. La polyvalence est beaucoup plus courante. L'hypothèse de Wigner (du nom d'Eugene Wigner, la phyisis qui a découvert l'universalité dans le spectre des atomes), suggère que tous les systèmes complexes avec corrélation sont universels, du réseau cristallin à Internet.

Plus le système est complexe, plus il se manifeste de manière universelle, explique Laszlo Erdös de l'Université de Munich, l'un des collègues de travail de Yao. "Vous croyez que l'universalité est un comportement typique."

Dans de nombreux systèmes simples, les composants individuels peuvent trop influencer le résultat global, ce qui modifie l'apparence du spectre. Les grands systèmes n'ont pas de dominance à un seul composant. "Il s'avère qu'il y a une pièce où beaucoup de gens décident de faire quelque chose, et l'identité de l'un d'eux n'est pas si importante", explique Wu.


Les mathématiciens utilisent des matrices aléatoires pour étudier et prédire certaines propriétés d'Internet, par exemple, la taille d'un cluster informatique typique

Lorsqu'un système fait preuve d'universalité, cela garantit qu'il est complexe et qu'il y a suffisamment de corrélation à l'intérieur pour être interprété comme une matrice aléatoire. «Cela signifie que vous pouvez utiliser une matrice aléatoire pour la modéliser», explique Wu. «Vous pouvez calculer d'autres paramètres de modèle sur la base de la matrice et les utiliser pour prédire le comportement de ce système.»

Cette technique permet aux scientifiques de comprendre la structure et l'évolution d'Internet. Certaines propriétés de cet immense réseau informatique, telles que la taille typique d'un cluster d'ordinateurs, peuvent être estimées assez précisément grâce aux propriétés mesurées de la matrice aléatoire correspondante. «Les gens sont intéressés par les clusters et leur emplacement, et cela est souvent dû à des objectifs pratiques, tels que la publicité», explique Wu.

Des technologies similaires peuvent conduire à des améliorations des modèles de changement climatique. Les scientifiques ont découvert que la présence d'universalité, similaire au spectre énergétique, dans le matériau indique une forte connectivité de ses parties et, par conséquent, une bonne conductivité des liquides, de l'électricité ou de la chaleur. Et vice versa, le manque de polyvalence peut indiquer la rareté du matériau et ses propriétés isolantes. Dans un nouvel article présenté lors d'une conférence mathématique à San Diego, Ken Golden, mathématicien à l'Université de l'Utah, et son étudiant, Ben Murphy, ont utilisé cette différence pour prédire la conductivité thermique et les flux de fluide dans la glace de mer, à la fois au niveau microscopique et Absinthe arctique, présente dans des territoires s'étendant sur des milliers de kilomètres.

La mesure spectrale de la mosaïque d'absinthe fondue, photographiée depuis un hélicoptère, ou les données de glace de mer obtenues à partir de l'échantillon, montrent l'état de chacun de ces systèmes. «L'écoulement de fluide à travers la glace de mer entraîne des processus très importants qui doivent être compris pour comprendre le système climatique», explique Golden. «Les transitions dans les statistiques de nos propres décisions représentent une nouvelle approche mathématiquement rigoureuse de l'inclusion de la glace de mer dans les modèles climatiques.»

La même astuce peut conduire à un simple test d'ostéoporose. Golden, Murphy et leurs collègues ont découvert que le spectre d'un os dense et sain est polyvalent, contrairement au spectre d'un os poreux.


Les armoises arctiques sont universelles si elles sont suffisamment connectées

«Nous travaillons avec des systèmes dont les« particules »peuvent être de taille millimétrique ou kilométrique, explique Murphy à propos des composants du système. "C'est incroyable que les mêmes calculs les décrivent tous."

La raison pour laquelle les systèmes réels présentent un comportement similaire à une matrice aléatoire est peut-être plus facile à comprendre dans le cas d'un noyau d'atomes lourds. Tous les systèmes quantiques, y compris les atomes, fonctionnent selon les règles des mathématiques, en particulier avec la participation de matrices. «C'est l'essence de la mécanique quantique», explique Freeman Dyson, un ancien physicien mathématique qui a aidé à développer la théorie de la matrice aléatoire dans les années 1960 et 1970 au Princeton Institute for Advanced Engineering. "Chaque système quantique est décrit par une matrice représentant son énergie totale, et les propres solutions de la matrice sont les niveaux d'énergie du système quantique."

Les matrices d'atomes simples, l'hydrogène et l'hélium, peuvent être calculées avec précision, et les solutions propres obtenues coïncident avec une précision surprenante avec les niveaux d'énergie mesurés des atomes. Mais les matrices de systèmes plus complexes, comme le noyau d'uranium, deviennent trop «épineuses» pour les «saisir». Selon Dyson, pour cette raison, ces noyaux peuvent être comparés à une matrice aléatoire. De nombreuses interactions au sein de l'uranium - éléments d'une matrice inconnue - sont si complexes que leur mélange produit du bruit, comme de nombreux sons superposés. En conséquence, la matrice inconnue qui contrôle le noyau se comporte comme une matrice avec des nombres aléatoires et leur spectre est universel.


Ces armoises non connectées n'ont pas d'universalité, leur spectre est aléatoire

Les scientifiques n'ont pas encore développé une compréhension intuitive des raisons pour lesquelles les systèmes complexes le démontrent, et pas une autre séquence aléatoire / périodique. "Nous ne savons cela que par les calculs", explique Wu. Un autre mystère est leur connexion avec la fonction zêta de Riemann, dans laquelle l'universalité se manifeste dans le spectre des zéros. Ces zéros sont étroitement liés à la distribution des nombres premiers - les entiers irréductibles qui composent le reste. Les mathématiciens recherchent depuis longtemps une description de la distribution des nombres premiers sur une droite numérique de 1 à l'infini, et l'universalité leur donne la clé. Certains pensent qu'une fonction zêta de Riemann peut être matricielle suffisamment complexe et cohérente pour posséder l'universalité. La découverte d'une telle matrice aurait une «forte influence» sur la compréhension de la distribution des nombres premiers, comme l'a dit Paul Bourgade, mathématicien à Harvard.

Il est possible que l'explication soit cachée encore plus profondément. "Il se peut que le centre de l'universalité et de la fonction zêta de Wigner ne soit pas la matrice, mais une structure mathématique qui n'a pas encore été découverte", explique Erdös. "Les matrices Wigner et les fonctions zêta peuvent être différentes représentations de cette structure."

Beaucoup de mathématiciens recherchent une réponse sans garantie d'une. «Personne n'imaginait que les bus de Cuernavac seraient un tel exemple. Personne n'imaginait que les zéros de la fonction zêta seraient un autre exemple, dit Dyson. "La beauté de la science est son imprévisibilité, et donc tout ce qui est utile vient de surprises."

Source: https://habr.com/ru/post/fr399535/