Des spécialistes des TI marchent sur des routes non pavées
Après des décennies de stagnation, de nouveaux raccourcis ont été trouvés pour le problème des vendeurs ambulants.
Il n'y a pas si longtemps, une équipe de chercheurs de Stanford et de l'Université McGill a battu le record de 35 ans d'informatique d'une quantité inimaginablement petite - de quatre centièmes de mille milliards de milliards de milliards de milliards de dollars. La percée - un problème de vendeur fait dans le problème des classiques de l'informatique - était trop petite pour une valeur pratique, mais il a insufflé une nouvelle vie à la recherche de solutions approximatives améliorées.La tâche est formée comme suit: pour un ensemble de villes reliées par des routes, il est nécessaire de trouver le chemin le plus court pour visiter chaque ville avec un retour au point de départ. Les solutions au problème ont des applications pratiques, du forage de trous dans des cartes de circuits imprimés à la gestion du calendrier des tâches sur un ordinateur et à l'organisation des propriétés du génome.Le problème du vendeur est facile à formuler et - en théorie - facile à résoudre en vérifiant tous les chemins fermés possibles pour trouver le plus court. Le problème avec l'approche par force brute est que lorsque le nombre de villes augmente, le nombre correspondant de chemins commence très rapidement à dépasser les capacités des ordinateurs les plus rapides. Pour dix villes, il y a plus de 300 000 itinéraires. Pour 15 villes, leur nombre s'élève à 87 milliards.Algorithme Christofides
Au début de l'ère informatique, les mathématiciens espéraient que quelqu'un trouverait une approche pratique du problème - un algorithme qui permettrait de le résoudre dans un délai raisonnable. Mais bien que les programmeurs aient progressé dans des cas spécifiques - en déterminant le chemin le plus court pour 49 villes dans les années 50, pour 2 392 villes dans les années 80 et pour 85 900 villes en 2006 - personne n'a proposé d'algorithme qui résout efficacement le problème dans le cas général. D'après le remarquable travail de 1972, il est possible qu'un tel algorithme n'existe pas du tout. L'informaticien Richard Karp de l'Université de Californie à Berkeley a montré que le problème du vendeur est NP-complet, ce qui signifie qu'il n'y a pas d'algorithme efficace (sauf si quelqu'un prouve que P = NP - mais la plupart des scientifiques pensent que ce n'est pas le cas) .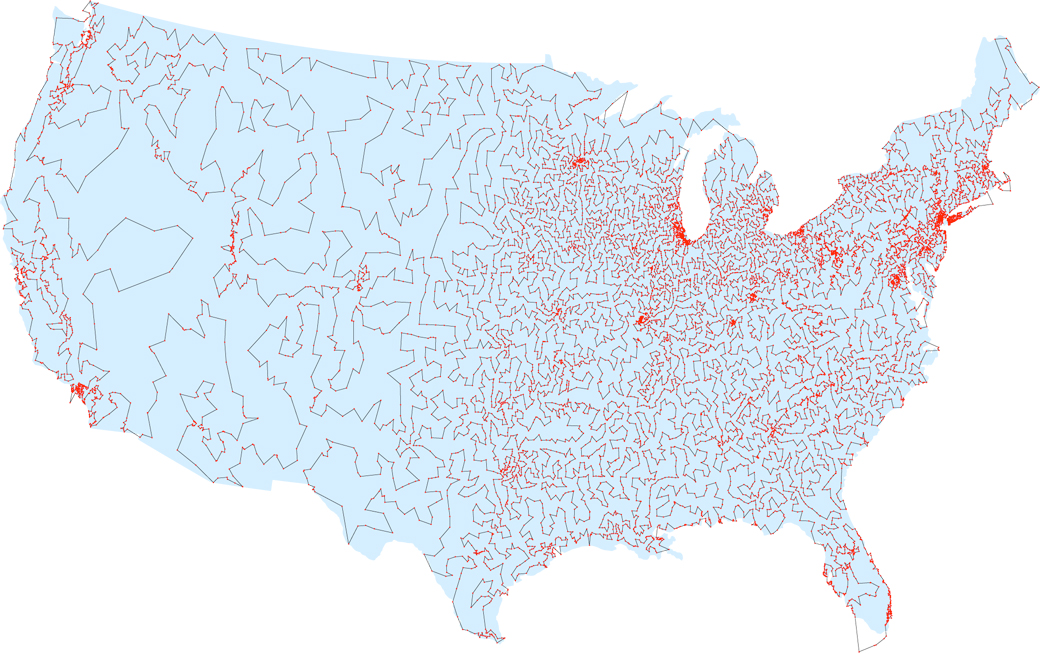
L'itinéraire le plus court à travers les 13509 villes des États-Unis avec une population de plus de 500 habitants (selon les données de 1998)Après la publication de Karp, de nombreux informaticiens ont commencé à développer un algorithme efficace pour trouver des solutions approximatives au problème - des chemins fermés dont la longueur n'est que légèrement plus longue que la plus courte. Et ici, ils ont eu plus de chance - en 1976, Nikos Christofides, professeur à l'Imperial College de Londres, a développé un algorithme qui produit des chemins qui ne dépasseront pas le chemin le plus court de plus de 50%.Après sa création, de nombreux scientifiques ont décidé que cet algorithme, qui est assez simple pour que les étudiants étudient en une heure, deviendra un lien intermédiaire, après quoi une solution vraie plus complexe et plus approximative sera trouvée. Mais des décennies plus tard, de tels algorithmes ne sont jamais apparus."Presque tous les étudiants en informatique ont passé des semaines ou des mois à essayer d'améliorer l'algorithme de Christofides", a déclaré Sanjeev Arora, scientifique à l'Université de Princeton.Enfin, en 2011, l'équipe de Stanford et McGill est allée au-delà de la garantie de 50% pour certains types de tâches de vendeur et a montré que leurs solutions ne dépasseraient pas le chemin le plus court de 49,99999999999999999999999999999999999999999999999999999999999999999999999999999696%.Depuis lors, un certain nombre d'algorithmes approximatifs améliorés sont apparus, grâce à un nouveau regard sur le problème. Bien que ces approximations ne s'appliquent qu'à certains types de tâches de vendeur itinérant, leur approche est assez prometteuse, selon Michael Gomans, spécialiste informatique au Massachusetts Institute of Technology.«Nous n'avons touché que légèrement la surface», dit-il. «Je crois que peut-être dans cinq ans, nous obtiendrons des résultats plus impressionnants.»Arbre le plus court
La Joconde comme chemin entre 100 000 villesL'algorithme Christofides ne commence pas par la recherche du chemin le plus court, mais par la recherche d'un arbre couvrant minimal - un ensemble de branches reliant les villes sans boucles fermées. Contrairement au chemin le plus court, l'arbre couvrant minimum est assez facile à construire - vous devez commencer par rechercher le chemin le plus court entre les deux villes; ce sera la première branche. Pour ajouter ce qui suit, vous devez trouver le chemin le plus court entre la nouvelle ville et l'une des deux précédentes - et ainsi de suite, jusqu'à ce que toutes les villes soient couvertes.L'arbre résultant n'est pas l'une des solutions possibles au problème du voyageur de commerce, car il ne nous donne pas un chemin fermé. Mais il peut être transformé en un tel chemin, en imaginant que les branches sont des murs, puis en marchant le long de l'arbre de sorte que votre doigt touche le mur jusqu'à ce que vous arriviez au début. La promenade qui en résulte traverse chaque ville et revient, mais généralement elle est loin du chemin le plus court, car elle passe plusieurs fois le long des mêmes segments - nous marchons deux fois chaque mur dans un arbre, une fois de chaque côté.Mais le chemin résultant dans le pire des cas n'est pas plus long que le chemin le plus court deux fois. En ajoutant des branches spécialement sélectionnées et en appliquant quelques astuces, Christofides a montré comment couper ce chemin pour qu'il ne dépasse pas le plus court de plus de 50%.Un arbre couvrant minimal est un point de départ naturel pour la construction d'une solution de contournement courte. Mais cette approche a également servi de point de départ pour les chercheurs essayant de faire valoir une garantie Christofides de 50%. Après tout, bien qu'un arbre couvrant minimal semble à première vue efficace, d'autres arbres peuvent être mieux adaptés au processus de conversion d'arbres en solution de contournement - par exemple, vous devez ajouter une seule jambe à un arbre sans ramification, afin qu'il devienne une solution de contournement.Le but était donc de trouver un arbre qui trouve un équilibre entre la longueur et la conversion simple en solution de contournement. Il n'y a pas d'algorithmes efficaces pour rechercher un arbre idéal (si P = NP n'est pas vrai), mais un algorithme approximatif réussi doit trouver seulement assez bon.Parcours fractionné
Le chemin vers un arbre «raisonnablement bon» comprenait une technique populaire, quoique contre-intuitive, qui reconnaissait des solutions fractionnaires pour des tâches spécifiques. Par exemple, une solution de contournement fractionnée peut inclure le déplacement à mi-chemin entre Minneapolis et Détroit, et à mi-chemin entre Cleveland et Détroit. D'un point de vue pratique, un tel chemin n'a pas de sens. Mais il peut être décrit avec précision mathématiquement, et contrairement au problème classique des vendeurs itinérants, une telle version fractionnée peut être résolue efficacement.De nombreux problèmes d'approximation en informatique peuvent être résolus en calculant des solutions pour la version fractionnée du problème, puis en arrondissant intelligemment les partages pour obtenir une solution approximative au problème d'origine. Mais jusqu'à récemment, personne n'avait encore compris comment procéder dans le cas du problème des vendeurs ambulants.En 2009, Amin Saberi de l'Université de Stanford et Arash Asadpour, alors étudiant diplômé, ont développé un schéma d'arrondi général qui utilise des nombres aléatoires pour sélectionner une solution entière qui préserve autant de propriétés de la solution fractionnée que possible. Saberi pensait que ce motif rappelait un "marteau lourd à la recherche d'un clou". Et il soupçonnait que la tâche du vendeur pourrait être le bon clou.Quelques mois plus tard, Saber, Asadpur, Gomans, l'étudiant diplômé de Stanford Shayan Gharan et Aleksander Madry, qui travaillent maintenant à l'École polytechnique fédérale de Lausanne en Suisse, ont montré que la nouvelle technique d'arrondi pouvait fournir un bon algorithme approximatif pour l'une des options tâches du vendeur, le cas "asymétrique". Un an plus tard, Saberi, Garan et Mohit Singh de l'Université McGill ont utilisé la même approche pour développer un nouvel algorithme approximatif pour le problème habituel des vendeurs ambulants.
Le problème de vendeur itinérant sollicité le plus important était le trajet entre 85 900 villes, calculé en 2006. L'emplacement des «villes» correspond à la conception d'une puce informatique spécifique créée dans le laboratoire de Bell, et la solution est le moyen le plus court pour le découper au laser.Ayant reçu une carte des villes et des itinéraires, le nouvel algorithme commence par calculer la solution fractionnaire exacte du problème du voyageur de commerce. Il arrondit ensuite cette solution à un arbre couvrant, qui devrait théoriquement se rapprocher d'un équilibre entre la longueur et la conversion simple en solution de contournement. Enfin, l'algorithme inclut cet arbre - et non l'arborescence minimale - dans le réseau Christofides.Le nouvel algorithme était «une idée que nous pourrions expliquer en quelques heures, mais sa preuve a pris environ un an», explique Saberi.Après une longue analyse, l'équipe de Stanford / McGill a pu améliorer l'algorithme de Christofides d'une petite fraction pour une large sous-classe de tâches de vendeur, «graphique». Quelques mois plus tard, d'autres équipes, inspirées par le succès, ont utilisé d'autres schémas d'arrondi pour obtenir des algorithmes pour le cas graphique avec de meilleures approximations. Le record actuel est de 40%, ce qui est bien mieux que 50% de Christofides.Le cas graphique "comprend bon nombre des mêmes difficultés que celles rencontrées dans le problème général", explique Arora, ajoutant que les schémas fonctionnant dans le cas graphique peuvent être utiles pour le problème général des vendeurs ambulants.Néanmoins, dit Sabre, résoudre le problème général approximatif des vendeurs nécessitera probablement de nouvelles idées. «Une découverte mathématique, c'est comme se déplacer dans une pièce sombre. Vous tendez la main et trouvez une chaise, tendez la main et trouvez une table », dit-il, pour paraphraser le mathématicien Andrew Wiles. «À un moment donné, la main trouve un interrupteur, et tout à coup, tout devient clair. Dans le cas de la tâche du vendeur, même après tant de travaux qui ont trouvé autant de limites du possible, je ne pense pas que nous ayons déjà trouvé cet interrupteur.Source: https://habr.com/ru/post/fr399873/
All Articles