Je ne mentirai pas, j'ai vraiment hâte au film Spider-Man: Homecoming [Spider-Man: Homecoming]. En attendant, le seul débouché pour moi sera de faire la physique de Spider-Man. Et je m'occuperai de ses nouvelles ailes de toile d'araignée vues dans la dernière bande-annonce.Pour les fans, je note que certaines des bandes dessinées originales sur Spider-Man ont vraiment montré comment il les utilise, bien qu'il ne les utilise pas toujours pour voler.Planification physique
Que se passe-t-il après que Spider-Man a sauté d'un bâtiment? Je peux simuler son mouvement en acceptant que trois forces agissent sur lui: la gravité, la résistance de l'air et la portance. Avec votre permission, je décrirai chacun d'eux.• Gravité - une force descendante constante proportionnelle à la masse de l'urgence (au moins à la surface de la Terre).• Résistance. Imaginez que vous tirez un objet à travers une mer géante de balles de ping-pong. Remplacez les balles par de l'air - et ce sera à peu près la même chose. La résistance augmente avec la vitesse.• Force de levage. Encore une fois, imaginez des collisions avec des balles, mais celles après lesquelles les balles rebondissent. En remplaçant les balles par de l'air, vous recevrez un ascenseur en fonction de l'angle d'attaque, de la surface et de la vitesse.Voici un beau diagramme des forces d'une personne qui planifie sur les ailes d'une urgence. Oui, alors que nous le modélisons avec un triangle.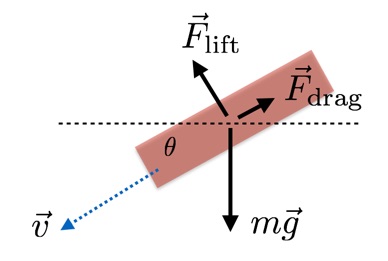 Dans notre modèle simple, la force de levage est perpendiculaire à la vitesse et la résistance est dirigée dans la direction opposée. Pour simuler le mouvement d'une urgence avec des ailes, j'ai besoin d'une formule pour les deux.
Dans notre modèle simple, la force de levage est perpendiculaire à la vitesse et la résistance est dirigée dans la direction opposée. Pour simuler le mouvement d'une urgence avec des ailes, j'ai besoin d'une formule pour les deux.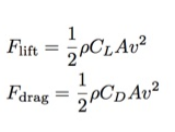 Ce sont des valeurs de forces qui sont importantes pour nous. Ils sont similaires, à l'exception de C L (coefficient de portance) et C D (coefficient de traînée). Dans les deux cas, ρ est la densité de l'air (1,2 kg / m 3 ) et v est la vitesse.Qu'est-ce que A? Il s'agit de la section transversale d'une personne (urgence dans notre cas). En théorie, A pour la résistance et pour la force de levage devrait différer, selon l'angle d'attaque. Mais je ne sais pas toujours exactement ce que je fais - c'est pourquoi j'ai vérifié auprès de différentes sources, et l'article de 2011 « La trajectoire d'un Batman qui tombe"du journal physique Journal of Physics Special Topics. Dans ce document, les auteurs ont utilisé la même zone pour la résistance et la portance, donc je ferai de même.
Ce sont des valeurs de forces qui sont importantes pour nous. Ils sont similaires, à l'exception de C L (coefficient de portance) et C D (coefficient de traînée). Dans les deux cas, ρ est la densité de l'air (1,2 kg / m 3 ) et v est la vitesse.Qu'est-ce que A? Il s'agit de la section transversale d'une personne (urgence dans notre cas). En théorie, A pour la résistance et pour la force de levage devrait différer, selon l'angle d'attaque. Mais je ne sais pas toujours exactement ce que je fais - c'est pourquoi j'ai vérifié auprès de différentes sources, et l'article de 2011 « La trajectoire d'un Batman qui tombe"du journal physique Journal of Physics Special Topics. Dans ce document, les auteurs ont utilisé la même zone pour la résistance et la portance, donc je ferai de même.Modélisation de trajectoire
Si une urgence saute d'un bâtiment, jusqu'où peut-elle aller en cas de chute? Quelle différence les ailes d'araignée lui donneront-elles? Modéliser l'état d'urgence n'est pas si simple, car la résistance et la portance dépendent de la vitesse. Une telle trajectoire ne peut être calculée qu'à l'aide d'un modèle numérique dans lequel le mouvement est divisé en petits pas.Faisons l'approximation. Tout d'abord, nous calculons la surface de l'urgence. Estimation approximative, j'ai obtenu: Ce qui nous donne une superficie d'environ 0,651 m 2 avec des ailes et 0,513 m 2 sans elles. Autres valeurs:• Coefficient de levage = 1,45 (la valeur est tirée du travail sur Batman)• Coefficient de résistance = 0,4 (au même endroit)• Poids = 64 kg• Vitesse initiale = 8 m / s (horizontal)• Et une autre hypothèse: un angle d'attaque constant, avec lequel les coefficients de traînée et de portance ne changent pas.Sans hésitation, je me suis lancé dans le monde des modèles numériques. J'ai laissé des commentaires dans le code afin que vous puissiez le refaire pour l'utiliser comme devoirs.
Ce qui nous donne une superficie d'environ 0,651 m 2 avec des ailes et 0,513 m 2 sans elles. Autres valeurs:• Coefficient de levage = 1,45 (la valeur est tirée du travail sur Batman)• Coefficient de résistance = 0,4 (au même endroit)• Poids = 64 kg• Vitesse initiale = 8 m / s (horizontal)• Et une autre hypothèse: un angle d'attaque constant, avec lequel les coefficients de traînée et de portance ne changent pas.Sans hésitation, je me suis lancé dans le monde des modèles numériques. J'ai laissé des commentaires dans le code afin que vous puissiez le refaire pour l'utiliser comme devoirs.GlowScript 2.1 VPython
A1=0.651
A2=0.513
g=vector(0,-9.8,0)
m=64
CL=1.45
CD=0.4
rho=1.2
v0=8
p=vector(v0,0,0)*m
p2=p
t=0
dt=0.01
h=40
r=vector(0,h,0)
r2=r
f1=series(color=color.red)
f2=series(color=color.blue)
while r.y>0:
v=p/m
v2=p2/m
Fd=-.5*rho*A1*CD*(mag(v)**2)*norm(v)
Fd2=-.5*rho*A2*CD*(mag(v2)**2)*norm(v2)
FL=-.5*rho*A1*CL*(mag(v)**2)*cross(norm(v),vector(0,0,1))
FL2=-.5*rho*A2*CL*(mag(v2)**2)*cross(norm(v2),vector(0,0,1))
F=m*g+Fd+FL
F2=m*g+Fd2+FL2
p=p+F*dt
p2=p2+F2*dt
r=r+p*dt/m
r2=r2+p2*dt/m
t=t+dt
f1.plot(r.x,r.y)
f2.plot(r2.x,r2.y)
print("Glide Ratio 1 = ",-p.x/p.y)
print("Glide Ratio 2 = ", -p2.x/p2.y)
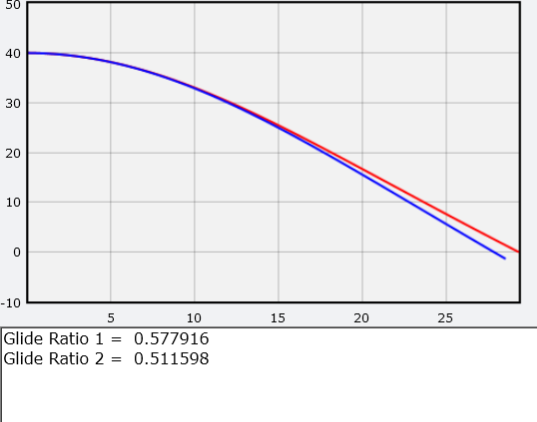 Dans mon modèle, la ligne rouge représente la trajectoire de l'urgence avec des ailes, et la ligne bleue sans ailes. Je tire également la valeur de la qualité aérodynamique. Puisqu'à la fin il se déplace à une vitesse constante, ce rapport sera simplement égal au rapport de la composante x de la quantité de mouvement divisée par la composante y.DevoirsUtilisez ce modèle numérique pour répondre aux questions suivantes . Ne vous inquiétez pas, vous ne casserez rien. Si vous faites quelque chose avec le code, redémarrez simplement et recommencez.• Selon Wikipedia, pour un parachutiste sautant en combinaison ailée, la qualité aérodynamique (le rapport portance / traînée) a une valeur de l'ordre de 2,5: 1 (c'est-à-dire que notre programme en déduirait le nombre 2,5). Pouvez-vous corriger le code afin que le programme produise une telle valeur? Astuce: modifiez la surface et la vitesse initiale.• Que faire si une urgence tombe verticalement? Quelle vitesse maximale gagnera-t-elle avec des ailes et sans elles?• À quelle vitesse l'urgence doit-elle se déplacer horizontalement pour qu'elle vole vers le haut plutôt que vers le bas au début du vol?• Un saut d'urgence peut-il viser vers le bas, afin de gagner en vitesse et de passer quelque temps en vol horizontal?• Pouvez-vous construire un modèle amélioré qui prend en compte l'angle d'attaque? Peut-être le pouvez-vous, mais il me semble que voler à basse vitesse est un sujet assez compliqué.
Dans mon modèle, la ligne rouge représente la trajectoire de l'urgence avec des ailes, et la ligne bleue sans ailes. Je tire également la valeur de la qualité aérodynamique. Puisqu'à la fin il se déplace à une vitesse constante, ce rapport sera simplement égal au rapport de la composante x de la quantité de mouvement divisée par la composante y.DevoirsUtilisez ce modèle numérique pour répondre aux questions suivantes . Ne vous inquiétez pas, vous ne casserez rien. Si vous faites quelque chose avec le code, redémarrez simplement et recommencez.• Selon Wikipedia, pour un parachutiste sautant en combinaison ailée, la qualité aérodynamique (le rapport portance / traînée) a une valeur de l'ordre de 2,5: 1 (c'est-à-dire que notre programme en déduirait le nombre 2,5). Pouvez-vous corriger le code afin que le programme produise une telle valeur? Astuce: modifiez la surface et la vitesse initiale.• Que faire si une urgence tombe verticalement? Quelle vitesse maximale gagnera-t-elle avec des ailes et sans elles?• À quelle vitesse l'urgence doit-elle se déplacer horizontalement pour qu'elle vole vers le haut plutôt que vers le bas au début du vol?• Un saut d'urgence peut-il viser vers le bas, afin de gagner en vitesse et de passer quelque temps en vol horizontal?• Pouvez-vous construire un modèle amélioré qui prend en compte l'angle d'attaque? Peut-être le pouvez-vous, mais il me semble que voler à basse vitesse est un sujet assez compliqué.