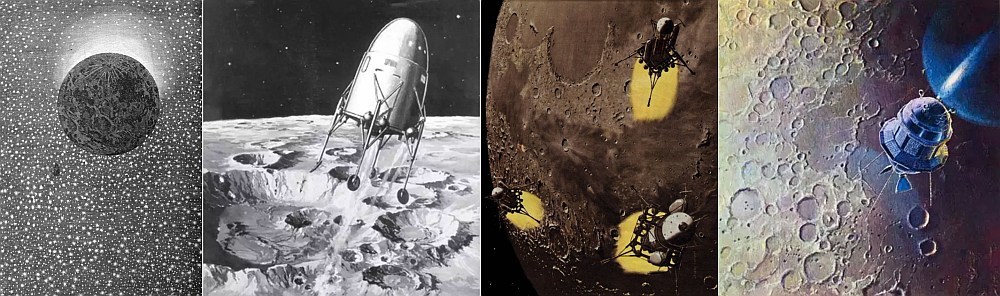
, , 1865 , « 97 20 ». , , , , .
, , , . , . , ! , , . , , «» . , .

, , . , , . , , , . , , . (, ), . , !
Pourtant, par exemple, peu de temps après la sortie du roman «Around the Moon», beaucoup doutaient de la possibilité d'une telle trajectoire d'un survol rapproché de la Lune sous l'influence de seules forces gravitationnelles. Ce n'est qu'au début du XXe siècle, lors de l'évaluation des orbites dans les systèmes d'étoiles binaires, que la possibilité de l'existence de telles orbites a été vraiment montrée. Voici ce que la revue anglaise «Knowledge» écrivait au début du XXe siècle dans l'article «Astronomie de Jules Verne»:«, . , . . , . , , . , , , . . . . , . , , , »., , , – , .
, , . - . , (1815-1871), ( IV). , ,
Leçons nouvelles de Cosmographie (1854). . ,
, , .
Henri Garcet (1815–1871)
, , , , « », . , «» 7 1869 , — .
:
— , , ?
— ? — .
— . , , , . : , , , .
— , — , — , , , , , .
— , , — .- - ?
— .
— ?
…
— , . :
, , , , , .
— ?
— . , , . , . .
— ?
— , « », ., :
où r est le rayon de la Terre, est la distance entre les centres de la Terre et de la Lune, x est la distance du noyau de la Terre. V 0 est la vitesse initiale du noyau. V est la vitesse à une distance de x.Et le vol ressemblait à çaIci, je voudrais noter que cette formule avec les données initiales indiquées est en effet vraie. Et il affiche vraiment avec précision l'effet gravitationnel de la Terre et de la Lune sur l'appareil à tout moment. Il est assez facile de dériver de la loi de conservation de l'énergie.Dérivation de la formule Verne-Garce
mv2 / 2 – γMm/R – γMm/R =const
m M,M – , ,
γ – , R - , R-
. .
mv2 / 2 – γMm/x– γMm/(D-x) =mv02 / 2 – γMm/r – γMm/(d-r)
m,
v2 / 2 –v02 / 2=γM/x+ γM/(D-x)– γM/r – γM/(d-r)
1/2*(v2-v02 )=γM(1/-1/r+M/M*1/(d-x)-M/M*1/(d-r))
1/2*(v2-v02 )=γM/r(r/-1+M/M(r/(d-x)-r/(d-r))
mg=mγM/r2 γM=g*r2
1/2*(v2-v02 )=gr(r/-1+M/M(r/(d-x)-r/(d-r))
? , . 1 /. . , , , , , . , - , . . , .
, . , , , . . , , . , , . . , 1759 .
On sait qu'Edmund Halley, compilant un catalogue de comètes, a remarqué que plusieurs comètes qui sont apparues dans le ciel à des moments différents ont des paramètres très similaires. Après les avoir vérifiés, il a décidé qu'il pourrait s'agir de la même comète. Ensuite, elle sera appelée par son nom. La comète Halley est apparue dans le ciel en 1531, 1607 et 1682. Autrement dit, la période de circulation était de 75 à 76 ans, et le scientifique a prédit la prochaine apparition pour 1758. Et tout serait merveilleux, sinon pour un «mais»: à l'heure estimée, la comète dans le ciel ne s'est jamais présentée.Ensuite, le mathématicien français Cleo a décidé de calculer sa trajectoire aussi précisément que possible. Y compris, en tenant compte des perturbations de sa trajectoire dues à l'attractivité de Jupiter et de Saturne. C'était un travail très fatigant et long, bien qu'il n'ait pas fait ce travail seul: il était assisté de l'astronome J. Lalande et de la mathématicienne Madame Lepot. Il s'est avéré que la différence avec les estimations précédentes de la période de révolution de la comète est de 618 jours, et elle arrivera à son périhélie le 13 avril 1759. Avec une erreur possible pendant un mois. Le bilan s'est avéré très précis: la comète a passé son périhélie le 12 mars. Ce fut à la fois une victoire pour les mathématiciens et une très bonne confirmation des lois de Newton.A propos de ce calcul, Laland a écrit plus tard: " , , , . , , — — 150 ".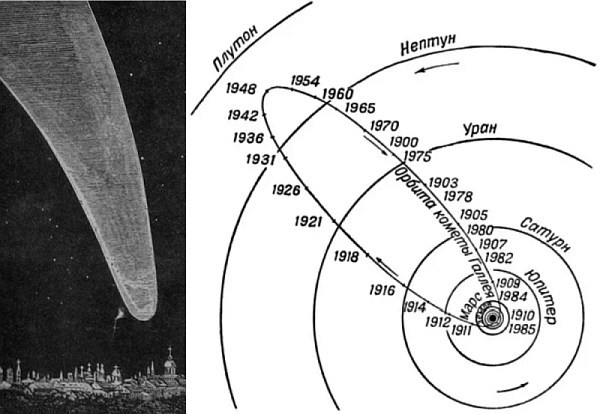
1829 , . –15 1835 . 16 , .
, . , . ! , , . , , , , , , . . . . , .
, , . , , .
, , , . , , . , , , , - .
« . ( )» 1928
: –
,
,
,
. , , , . . , - , ; , , . , , .
18 1952 . , , , .
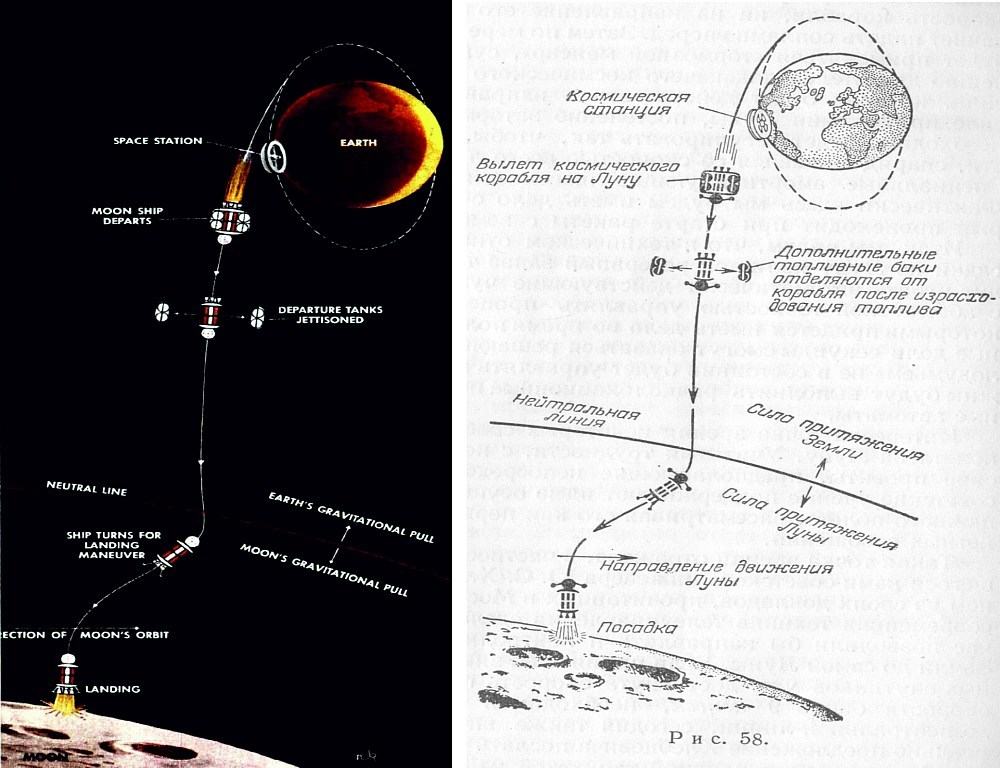
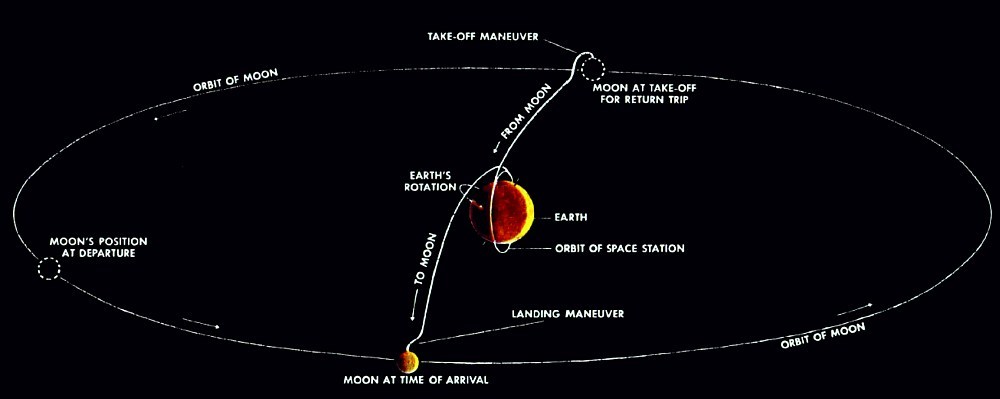
, : , – . , . .
. , - .
.