En novembre, le magazine Quanta a intrigué ses lecteurs avec des questions concernant le dessin de formes à partir d'objets plats identiques (tels que des pièces de monnaie ou des dominos). Cet article fournit à la fois des questions et des réponses détaillées.Question 1
, , . . . , , ? n ?
Physiquement, la tâche nécessite d'équilibrer le couple de la figure des deux côtés du bord de la table. Le couple de chaque côté est le produit de la masse de ce côté et de la distance du centre de masse au bord. Lorsque le centre de masse de la figure entière est au-dessus du bord, le même moment agit des deux côtés et le couple total du système est nul. Pour un objet composé, le couple total pour n'importe quelle face peut être trouvé en ajoutant le couple de tous les composants. Par conséquent, nous pouvons diviser et régner sur la tâche d'origine, en ne considérant que les changements qui se produisent lorsqu'un nouveau bloc est ajouté à une pile existante, quelque chose comme l'induction mathématique (appelons cela l'induction physique).Considérons une pile de n-1 blocs, dont chacun pèse une unité de poids et a une longueur d'une unité de longueur. La pile est équilibrée au bord de la table. Imaginez que la ligne de visée est dirigée le long du bord de la table et que la table est à gauche - c'est-à-dire que les extrémités suspendues des blocs dépassent vers la droite. Étant donné que l'empilement est équilibré au bord, le centre de masse est juste au-dessus du bord et son couple est nul. Imaginez maintenant que nous avons soulevé la pile entière verticalement et placé un autre bloc en dessous de sorte que son bord droit soit aligné avec le bord de la table. En pratique, cela peut être difficile, mais dans une expérience de pensée, c'est simple.Nous avons ajouté une certaine stabilité à la pile en ajoutant le nième bloc à partir du bas, car le centre de masse de la pile entière s'est légèrement décalé vers la gauche. Notons ce décalage x. n blocs pèsent n unités, et ils ont un couple commun x * n autour du bord de la table, dirigé vers la gauche. Rappelons qu'une pile de n-1 blocs a un moment zéro total. Nous n'avons ajouté que le moment du nouveau bloc - avec une masse d'une unité de masse et avec une distance au centre de masse du bord de la table sur une demi-unité de longueur.Il s'avère que x * n = 1/2, ce qui signifie x = 1 / 2n, où x est la distance entre le nouveau centre de masse et le bord de la table.Cela signifie que si vous déplacez la pile entière de n blocs vers la droite de 1/2 de longueur, elle sera parfaitement équilibrée au bord - et c'est le décalage maximal possible. Pour terminer la construction de l'induction, on note que le porte-à-faux maximum du premier bloc à partir du bord de la table est de 1/2 unité de longueur.Par conséquent, pour cinq blocs, nous substituons dans la formule n pour chaque niveau de 1 à cinq pour obtenir le porte-à-faux maximum:x=1/2+1/4+1/6+1/8+1/10=137/120=1,141(6)
On peut voir que si vous commencez par le haut puis ajoutez des blocs vers le bas, chaque décalage correspondra à la moitié de l'inverse du nombre de blocs disponibles. De telles séquences de nombres inverses sont appelées séries harmoniques. Une telle série diverge lentement, et comme n tend vers l'infini, elle tend aussi vers l'infini.La formule de somme générale pour n blocs est obtenue en additionnant tous les membres de la série. Il s'avère que la moitié du nième terme harmonique, qui peut s'écrire:Question 2
Imaginez que vous ayez les mêmes cinq blocs et que vous vouliez mettre une décoration tout en haut, à un point qui est un quart de la longueur du bloc de l'extrémité suspendue. Tous les blocs pèsent une unité de poids et les bijoux pèsent un cinquième du bloc. Quelle est la longueur maximale du porte-à-faux maintenant? Comment cela change-t-il la formule de base?
Tout d'abord, considérez le premier bloc avec la décoration posée dessus, et couché de sorte que son bord droit affleure le bord de la table. Le centre de masse du bloc sans décoration est à une demi-unité de longueur du bord de la table. La décoration le déplacera vers la droite, disons, de x. La masse de la décoration est de 1/5 et sa distance du nouveau centre de masse sera de 1/4. Nous égalisons les moments et obtenons x = 1/5 * (1/4 x), donc, x = 1/24. En raison de la décoration, il est nécessaire de déplacer le premier bloc vers la gauche de 1/24 de la longueur, de sorte que le porte-à-faux maximum est maintenant de 11/24 au lieu de 1/2.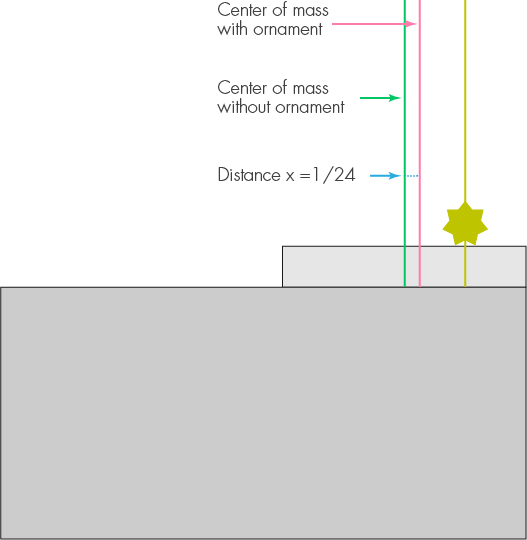
Question 3
, , . . . , . , , . , ?
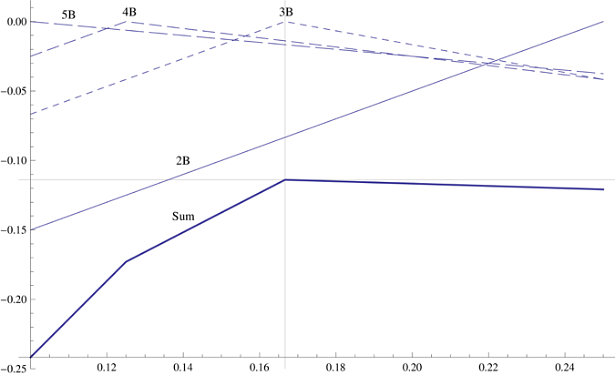
Étant donné que la probabilité d'avoir deux à cinq blocs est la même, vous devez maximiser le montant indiquant le porte-à-faux maximal pour ces quatre cas. Pour une pile de 2 à 5 blocs, il y a une position optimale du premier bloc, donnant le porte-à-faux maximum de la pile entière. Si vous créez le plus grand porte-à-faux sur le graphique pour chacune des quatre tailles possibles de la pile suivante, vous obtenez deux graphiques linéaires et deux graphiques sous la forme d'un V. inversé. Leurs sommets indiquent la position de départ optimale du bloc initial pour des piles de 3-4 blocs. Pour résumer les graphiques, nous obtenons le graphique global de surplomb, qui change radicalement de direction dans chacune des quatre positions optimales. Il s'avère que le meilleur porte-à-faux global est atteint dans la position optimale pour les trois blocs, après quoi le graphique descend. Par conséquent, vous devez placer le bloc d'origine sous l'hypothèseque vous recevrez trois blocs supplémentaires, et le surplomb sera de 1/6 unités de longueur.