Il y a 70 ans, le 16 décembre 1947, dans les laboratoires Bell Labs, John Bardin et Walter Brattain, sous la direction de William Shockley, ont créé le premier transistor bipolaire opérationnel. Le 23 décembre, Brattain a présenté à ses collègues le premier amplificateur à transistor. Par conséquent, ce jour est souvent appelé Transistor Day . Il n'est pas nécessaire de parler de l'importance de cet événement. Le transistor est considéré comme l'une des inventions les plus importantes du XXe siècle, sans lequel les ordinateurs fonctionneraient encore sur les lampes et les relais et occuperaient des bâtiments entiers. Shockley, Bardin et Brattain ont reçu le prix Nobel de physique pour leur travail en 1956. Au fil des ans, le transistor s'est miniaturisé à seulement quelques atomes. Chaque processeur possède des milliards de transistors, de sorte que le transistor peut être appelé le périphérique le plus massif créé par l'humanité.Mais quel genre de travail le transistor fait-il pour nous? Allons dans un voyage mental: nous allons tracer le chemin depuis le bout des doigts de haut niveau jusqu'à notre anniversaire - le transistor.Que prendre comme point de départ? Eh bien, dessinez au moins un bouton habrakat.
Il n'est pas nécessaire de parler de l'importance de cet événement. Le transistor est considéré comme l'une des inventions les plus importantes du XXe siècle, sans lequel les ordinateurs fonctionneraient encore sur les lampes et les relais et occuperaient des bâtiments entiers. Shockley, Bardin et Brattain ont reçu le prix Nobel de physique pour leur travail en 1956. Au fil des ans, le transistor s'est miniaturisé à seulement quelques atomes. Chaque processeur possède des milliards de transistors, de sorte que le transistor peut être appelé le périphérique le plus massif créé par l'humanité.Mais quel genre de travail le transistor fait-il pour nous? Allons dans un voyage mental: nous allons tracer le chemin depuis le bout des doigts de haut niveau jusqu'à notre anniversaire - le transistor.Que prendre comme point de départ? Eh bien, dessinez au moins un bouton habrakat.HTML et CSS
Un bouton se compose de pixels d'arrière-plan, de texte et d'une bordure. Dans le code, défini par la balise <a>, auquel les règles de disposition CSS sont appliquées. Par exemple, une règle CSS est appliquée à une bordure aux coins arrondis:border-radius: 3px;
 Ainsi, la frontière se compose de quatre segments et de quatre arcs («quarts» d'un cercle).
Ainsi, la frontière se compose de quatre segments et de quatre arcs («quarts» d'un cercle).Navigateur
Pour la recherche, j'ai pris mon Firefox préféré. Avant que FF ne commence à dessiner notre bouton, il doit faire beaucoup de travail sur l'analyse et le calcul de la position des éléments:- Télécharger du HTML sur un réseau, analyser, composer une arborescence DOM
- Téléchargez sur le réseau CSS, effectuez une analyse lexicale, analysez
- Lier des règles basées sur la priorité et l'héritage aux éléments de la page
- Pour tous les nœuds DOM visibles, composez un arbre de leurs zones rectangulaires - cadres.
- Pour les cadres, calculez les dimensions et l'emplacement (voir la vidéo )
- Composez des calques à partir de cadres en tenant compte du z-index et du type de contenu (<canvas>, SVG, <video>).
- Créez une liste de dessins dans l'ordre: couleur d'arrière-plan, image d'arrière-plan, bordure, descendants, contour.
Ajouter. matériel de lecture: Nous ne nous attarderons pas sur ces étapes en détail. Après eux vient le dessin réel des éléments nécessaires.Le fichier nsCSSRenderingBorders.cpp est responsable du dessin des bordures . Et la fonction générale du dessin des bordures s'appelle (qui aurait pensé): DrawBorders () . La fonction sélectionne la méthode de rendu optimale pour diverses situations. Nous avons un cas relativement simple: il y a un rayon de bordure, mais les bordures de tous les côtés sont solides et de la même couleur.Notre siif (allBordersSame &&
mCompositeColors[0] == nullptr &&
mBorderStyles[0] == NS_STYLE_BORDER_STYLE_SOLID &&
!mAvoidStroke &&
!mNoBorderRadius)
{
gfxRect outerRect = ThebesRect(mOuterRect);
RoundedRect borderInnerRect(outerRect, mBorderRadii);
borderInnerRect.Deflate(mBorderWidths[eSideTop],
mBorderWidths[eSideBottom],
mBorderWidths[eSideLeft],
mBorderWidths[eSideRight]);
RefPtr<PathBuilder> builder = mDrawTarget->CreatePathBuilder();
AppendRoundedRectToPath(builder, mOuterRect, mBorderRadii, true);
AppendRoundedRectToPath(builder, ToRect(borderInnerRect.rect), borderInnerRect.corners, false);
RefPtr<Path> path = builder->Finish();
mDrawTarget->Fill(path, color);
return;
}
Il existe des options beaucoup plus complexes, telles que l'ancrage dans les coins avec le rayon de bordure de différents types de bordures en pointillés et en pointillés, voir DrawDashedOrDottedCorner () . Il en code complètementMais revenons à notre if. À partir du commentaire, nous apprenons que dans ce cas, la bordure est dessinée à l'aide de deux rectangles - interne et externe, puis le chemin créé (chemin) est rempli de la couleur souhaitée.AppendRoundedRectToPath(builder, mOuterRect, mBorderRadii, true);
AppendRoundedRectToPath(builder, ToRect(borderInnerRect.rect), borderInnerRect.corners, false);
RefPtr<Path> path = builder->Finish();
mDrawTarget->Fill(path, color);
Accédez à AppendRoundedRectToPath () dans gfx / 2d / PathHelpers.cpp.Encore une fois, nous fixons des points d'arrêt Nous apprenons du commentaire sur la fonction que les coins sont dessinés en quatre points de contrôle par des courbes de Bézier . Les courbes de Bézier sont souvent utilisées en infographie, y compris pour dessiner des arcs de cercles et d'ellipses. Comme nous en apprenons davantage dans le commentaire, il existe de nombreuses options pour choisir des points de contrôle pour construire une courbe. Dans ce cas, nous avons besoin que les points 0 et 3 appartiennent aux côtés du rectangle, les points 0, 1 et C se trouvent sur une ligne droite, les points 3, 2 et C sur l'autre. Voir la figure: Il nous reste à calculer le rapport des longueurs des segments 01 / 0C et 32 / 3C. Ici, les auteurs utilisent des calculs approximatifs et obtiennent la constante magique alpha:
Il nous reste à calculer le rapport des longueurs des segments 01 / 0C et 32 / 3C. Ici, les auteurs utilisent des calculs approximatifs et obtiennent la constante magique alpha:const Float alpha = Float(0.55191497064665766025);
Malheureusement, les articles avec l'algorithme de sélection des points de contrôle référencé par le commentaire ne sont pas dans le domaine public. Mais en général, il convient de noter qu'en infographie, les algorithmes utilisent souvent l'approximation pour améliorer les performances. Par exemple, l' algorithme de Brezenham vous permet de dessiner des segments et des cercles non "dans le front" - en résolvant les équations y = f (x), mais avec des opérations entières plus astucieuses. Même chose avec le remplissage, etc.Plus loin dans le cycle, nous allons d'un coin à l'autre, utilisons alpha pour calculer les coordonnées des points de contrôle et, enfin, appelons les fonctions de dessin de la ligne de frontière et de l'arc du coin:aPathBuilder->LineTo(p0);
aPathBuilder->BezierTo(p1, p2, p3);
Ajouter. matériel de lecture Code AppendRoundedRectToPath () completvoid
AppendRoundedRectToPath(PathBuilder* aPathBuilder,
const Rect& aRect,
const RectCornerRadii& aRadii,
bool aDrawClockwise)
{
const Float alpha = Float(0.55191497064665766025);
typedef struct { Float a, b; } twoFloats;
twoFloats cwCornerMults[4] = { { -1, 0 },
{ 0, -1 },
{ +1, 0 },
{ 0, +1 } };
twoFloats ccwCornerMults[4] = { { +1, 0 },
{ 0, -1 },
{ -1, 0 },
{ 0, +1 } };
twoFloats *cornerMults = aDrawClockwise ? cwCornerMults : ccwCornerMults;
Point cornerCoords[] = { aRect.TopLeft(), aRect.TopRight(),
aRect.BottomRight(), aRect.BottomLeft() };
Point pc, p0, p1, p2, p3;
if (aDrawClockwise) {
aPathBuilder->MoveTo(Point(aRect.X() + aRadii[RectCorner::TopLeft].width,
aRect.Y()));
} else {
aPathBuilder->MoveTo(Point(aRect.X() + aRect.Width() - aRadii[RectCorner::TopRight].width,
aRect.Y()));
}
for (int i = 0; i < 4; ++i) {
int c = aDrawClockwise ? ((i+1) % 4) : ((4-i) % 4);
int i2 = (i+2) % 4;
int i3 = (i+3) % 4;
pc = cornerCoords[c];
if (aRadii[c].width > 0.0 && aRadii[c].height > 0.0) {
p0.x = pc.x + cornerMults[i].a * aRadii[c].width;
p0.y = pc.y + cornerMults[i].b * aRadii[c].height;
p3.x = pc.x + cornerMults[i3].a * aRadii[c].width;
p3.y = pc.y + cornerMults[i3].b * aRadii[c].height;
p1.x = p0.x + alpha * cornerMults[i2].a * aRadii[c].width;
p1.y = p0.y + alpha * cornerMults[i2].b * aRadii[c].height;
p2.x = p3.x - alpha * cornerMults[i3].a * aRadii[c].width;
p2.y = p3.y - alpha * cornerMults[i3].b * aRadii[c].height;
aPathBuilder->LineTo(p0);
aPathBuilder->BezierTo(p1, p2, p3);
} else {
aPathBuilder->LineTo(pc);
}
}
aPathBuilder->Close();
}
Mais alors tout dépend du backend des graphiques 2D que Mozilla utilise.Moteur graphique
Gecko utilise la bibliothèque Moz2D indépendante de la plate-forme, qui à son tour peut utiliser l'un des backends: Cairo, Skia, Direct2D, Quartz et NV Path. Par exemple, Direct2D, Cairo, Skia sont disponibles pour Windows. Skia est également le backend Chromium. Vous pouvez changer le backend dans about: config. Les backends, à leur tour, peuvent tout lire sur le CPU, ou ils peuvent utiliser l'accélération matérielle GPU dans une certaine mesure. Par exemple, Skia a son propre backend OpenGL - Ganesh.Le code Direct2D est fermé, nous ferions donc mieux d'activer Skia et de voir ce qu'il fait. La fonction pour dessiner une courbe cubique SkPath :: cubicTo est appelée. Pour construire une courbe, elle est divisée par l'algorithme de Castelljo en un certain nombre de segments droits, qui sont réellement dessinés (voir core / SkGeometry.cpp).Ajouter. matériel de lecture Code machine
Pour être honnête, je n'ai pas réussi à comprendre pleinement les internes de Skia, j'ai donc pris un peu de recul - vers AppendRoundedRectToPath (), où toutes les opérations sont effectuées sur des entiers - ce qui pourrait être plus facile?Après avoir ouvert le code désassemblé, il faut y trouver l'opération d'addition....
142B1863 00 00 add byte ptr [eax],al
142B1865 00 8D 43 FF 0F 84 add byte ptr [ebp-7BF000BDh],cl
142B186B 67 01 00 add dword ptr [bx+si],eax
142B186E 00 99 0F 57 C9 F7 add byte ptr [ecx-836A8F1h],bl
142B1874 F9 stc
142B1875 8B C3 mov eax,ebx
142B1877 8B CA mov ecx,edx
142B1879 99 cdq
142B187A F7 7C 24 28 idiv eax,dword ptr [esp+28h]
...
Ouais! Même une personne aussi éloignée de l'ASM que je peux facilement deviner que l'opération ADD est responsable de l'ajout. Effectuez la première opération:142B1863 00 00 add byte ptr [eax],al0x142B1863 - adresse dans la RAM0x00 - opcode - code d'instruction du processeur. Ce Mozilla compilé sous x86, et en ouvrant la table d'instructions x86 , nous verrons que le code 00 signifie une opération d'ajout 8 bits avec des mnémoniques ADD. Le premier opérande peut être un registre ou une cellule mémoire à accès aléatoire, le second peut être un registre. Le premier opérande est ajouté au second, le résultat est écrit dans le premier. Je vais expliquer, au cas où, que le registre est une mémoire RAM ultrarapide à l'intérieur du processeur, par exemple, pour stocker des résultats de calcul intermédiaires.Le deuxième octet est également 0x00 et est appelé MOD-REG-R / M. Ses bits spécifient les opérandes et la méthode d'adressage. MOD = 00b en combinaison avec R / M = 000b signifie que l' adressage indirect est utiliséREG = 000b signifie que le registre AL est utilisé (les 8 bits inférieurs du registre EAX)[eax] - indique que l'ajout est effectué avec la cellule RAM, dont l'adresse est dans le registre EAX.Comment le processeur traite-t-il la commande ADD?
MOD = 00b en combinaison avec R / M = 000b signifie que l' adressage indirect est utiliséREG = 000b signifie que le registre AL est utilisé (les 8 bits inférieurs du registre EAX)[eax] - indique que l'ajout est effectué avec la cellule RAM, dont l'adresse est dans le registre EAX.Comment le processeur traite-t-il la commande ADD?CPU
Sur la base de la description de la microarchitecture Skylake , j'ai compilé une liste (extrêmement simplifiée) d'étapes:- Les instructions X86 sont extraites d'un cache d'instructions L1 de 32 Ko dans un tampon de précodage de 16 octets
- Les commandes précodées sont organisées dans la file d'instructions (taille 2x25) et pénètrent dans les décodeurs
- x86 1-4 (µOPs). ADD 1 µOP ALU (- ) 2 µOP AGU ( ) (., ). 86 .
- Allocation Queue (IDQ). , Loop Stream Detector — .
- : , . . .
- La micro-opération est confiée au gestionnaire Unified Scheduler, qui décide à quel moment et à quel port envoyer les opérations à exécuter dans l'ordre de réception. Derrière chaque port se trouve un actionneur. Nos micro-opérations iront à ALU et AGU.
 Le cœur de SkyLake. Image de en.wikichip.org .Je le répète, c'est ma description très simplifiée et ne prétend pas être exacte et complète. Pour plus de référence, je recommande de lire le post Journey Through the Computing Processor Processor et l'article Processors from the Intel Core i7 Family
Le cœur de SkyLake. Image de en.wikichip.org .Je le répète, c'est ma description très simplifiée et ne prétend pas être exacte et complète. Pour plus de référence, je recommande de lire le post Journey Through the Computing Processor Processor et l'article Processors from the Intel Core i7 FamilyALU
Il serait maintenant intéressant de savoir ce qui se passe à ALU: comment les chiffres sont-ils additionnés? Malheureusement, les informations sur la mise en œuvre spécifique de la microarchitecture et de l'ALU sont le secret commercial d'Intel, nous revenons donc à la théorie plus tard.Un dispositif pour ajouter deux bits binaires (c'est-à-dire un bit) est appelé additionneur . La sortie est la somme et le bit de retenue. Source: WikipédiaDepuis dans la vie réelle, nous devons ajouter des nombres composés de plusieurs chiffres, l'additionneur doit également accepter le bit de retenue du chiffre précédent comme entrée. Un tel additionneur est appelé plein .
Source: WikipédiaDepuis dans la vie réelle, nous devons ajouter des nombres composés de plusieurs chiffres, l'additionneur doit également accepter le bit de retenue du chiffre précédent comme entrée. Un tel additionneur est appelé plein .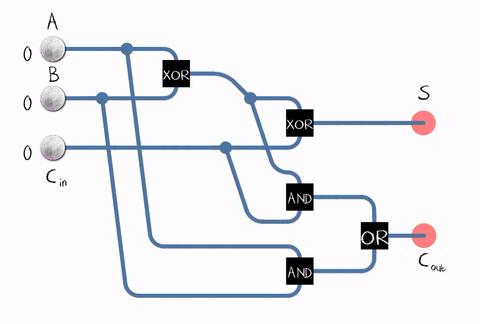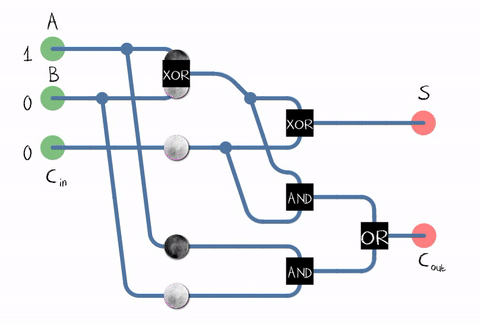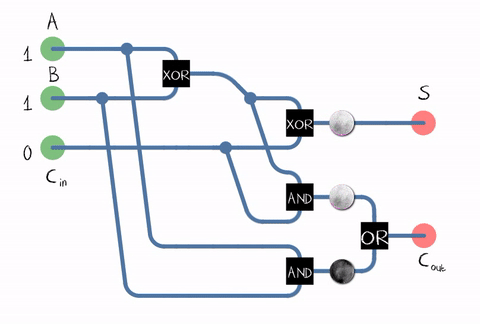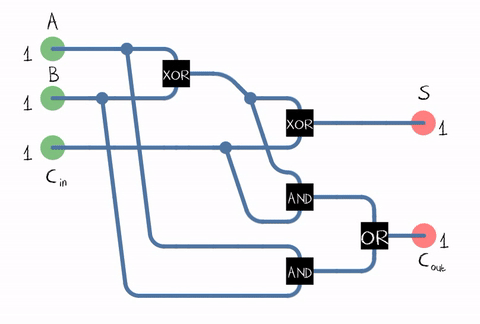 Source: WikipediaComme le montre la figure, l'additionneur est composé d'éléments logiques: XOR, AND, OR. Et chaque élément logiquepeut être implémenté à l' aide de plusieurs transistors. Ou même un relais .
Source: WikipediaComme le montre la figure, l'additionneur est composé d'éléments logiques: XOR, AND, OR. Et chaque élément logiquepeut être implémenté à l' aide de plusieurs transistors. Ou même un relais . Un exemple d'implémentation d'un additionneur complet sur les transistors CMOS . SourceNous sommes donc arrivés au transistor! Bien que, bien sûr, non seulement les ALU fonctionnent sur les transistors, mais aussi sur d'autres unités de processeur, mais la plupart des transistors sont utilisés dans le cache comme ses cellules.En réalité, le circuit additionneur de notre processeur peut être construit différemment et être beaucoup plus compliqué. Par exemple, il y a 45 ans déjà, Intel 8008 était en mesure de calculer tous les bits de retenue à l'avance afin d'effectuer l'addition en parallèle (le soi-disant additionneur avec report parallèle). Peu importe, lisez l'intéressant article de blog sur la rétro-ingénierie ALU Intel 8008 dans le blogKen Shirriff. C'est-à-dire Diverses optimisations sont utilisées: par exemple, la multiplication est également bénéfique à ne pas faire de front.
Un exemple d'implémentation d'un additionneur complet sur les transistors CMOS . SourceNous sommes donc arrivés au transistor! Bien que, bien sûr, non seulement les ALU fonctionnent sur les transistors, mais aussi sur d'autres unités de processeur, mais la plupart des transistors sont utilisés dans le cache comme ses cellules.En réalité, le circuit additionneur de notre processeur peut être construit différemment et être beaucoup plus compliqué. Par exemple, il y a 45 ans déjà, Intel 8008 était en mesure de calculer tous les bits de retenue à l'avance afin d'effectuer l'addition en parallèle (le soi-disant additionneur avec report parallèle). Peu importe, lisez l'intéressant article de blog sur la rétro-ingénierie ALU Intel 8008 dans le blogKen Shirriff. C'est-à-dire Diverses optimisations sont utilisées: par exemple, la multiplication est également bénéfique à ne pas faire de front.Conclusions: qu'avons-nous appris?
- C'est compliqué
- Cela est clairement démontré: pour résoudre le problème de la complexité excessive, les ingénieurs utilisent la division de systèmes complexes en niveaux (couches).
- Les architectures à plusieurs niveaux offrent une portabilité: par exemple, Firefox peut fonctionner sur différents systèmes d'exploitation et sur différents matériels.
- L'interaction entre les niveaux est due à l'ouverture des spécifications des interfaces, des services et des formats de données, par exemple HTML et CSS, C ++, un ensemble de commandes x86, etc.
- Notre héros du jour travaille tout en bas - un transistor .
PS Je suis un amateur (développeur web), et je connais un peu l'architecture C ++, ASM, BT - du cours de l'institut, je pourrais gâcher quelque chose. N'hésitez pas à envoyer des commentaires.