🛂 🛀 📭 Rééchantillonnage. Mur de briques numérique contre la théorie du complot. Conte de Noël pour les amateurs de son clair 🧘🏻 🐘 🕺🏼

Aucun mythe n'a accumulé autant de mythes
que dans le domaine des appareils Hi-Fi et Hi-End pour reproduire le son.
Hit Christmas Story sur l'un d'eux!

Quand la vieille année était déjà passée, le Nouvel An était d'abord accueilli dans un cercle familial étroit, puis avec des parents plus éloignés, lorsque les salades du Nouvel An se terminaient ou devenaient sans valeur et commençaient à libérer une gueule de bois ...

Ceux qui ne voulaient pas ~~ou ne pouvaient pas~~ célébrer le Nouvel An à l'étranger commencent Ressentez l'appel d'un ordinateur personnel.

C'est pour eux que mon histoire de Noël porte sur les bases du rééchantillonnage - une technologie qui a considérablement amélioré la qualité de lecture des CD audio au début du millénaire. C'est alors que les convertisseurs numérique-analogique 18 et même 20 bits ont commencé à être utilisés pour lire des enregistrements 16 bits. À première vue, cela ressemblait à un stratagème marketing de fabricants visant à extraire une partie supplémentaire de l'argent des portefeuilles d'audiophiles crédules, mais cette fois, les partisans de la théorie du complot peuvent fumer de côté. En fait, c'était une tentative réussie d'améliorer la qualité de la reproduction et de réduire le prix de l'équipement professionnel coûteux. L'histoire est ancienne, mais instructive, à bien des égards pertinente à ce jour.

Le DAC numérique-analogique est le cœur de tout système de production audio qui utilise des CD comme source. Il lui est confié la tâche complexe et délicate de décoder une séquence de nombres à 16 bits et de la convertir en un format perçu par l'oreille humaine.

En 1983, le premier lecteur CD culte Magnavox emblématique est apparu avec un double convertisseur 14 bits, mais au début du siècle, de nombreux systèmes de lecture de CD de haute qualité avaient des convertisseurs 18 ou 20 bits. Pourquoi?

Un peu de théorie, presque sans formules

Le concept de conversion numérique-analogique repose sur deux piliers: la fréquence d'échantillonnage d' échantillonnage et la profondeur de bits de quantification .

Pour lire le son au format PCM, nous devons à intervalles réguliers convertir les valeurs numériques en leurs valeurs analogiques de tension ou de courant correspondantes. La fréquence de ces transformations est la fréquence d'échantillonnage. Selon le théorème de Nyquist, il est ainsi possible de reproduire des signaux avec une fréquence ne dépassant pas la moitié de la fréquence d'échantillonnage. Les formats les plus courants qui sont capables de reproduire des signaux avec une fréquence perçue par l'oreille humaine, le ~~chiffre généralement accepté est de 20 kHz~~ , ont des fréquences d'échantillonnage de 44,1 et 48 kHz.

Le premier est encore largement utilisé dans les disques compacts audio (CDDA, Eng. Compact Disc Digital Audio, également appelé Eng. Audio CD et Red Book), et le second est né dans un certain nombre de normes pour les appareils d'enregistrement professionnels.

Imaginons que lors de l'enregistrement, un signal audio frappe un convertisseur analogique-numérique idéal. Il n'a pas de bruit et de distorsion propres et convertit la valeur instantanée du signal qui y arrive en numérique avec une profondeur de bits donnée, par exemple 16 bits, comme c'est la coutume au format CD audio. Dans ce cas, la plage dynamique théoriquement réalisable du signal (le rapport entre les signaux numérisés avec les niveaux le plus élevé et le plus bas) sera de 98,1 dB. Pour calculer cette valeur, une formule approximative est souvent utilisée, selon laquelle chaque bit supplémentaire ajoute 6 décibels à la plage dynamique théoriquement réalisable. Pour un signal 16 bits, nous obtenons: 6

dB / bit * 16 bits = 96 dB .

Un vrai signal musical n'est le plus souvent pas un son pur, mais un mélange d'un grand nombre d'harmoniques changeant rapidement de fréquence et d'amplitude. Pour les harmoniques ayant une amplitude inférieure à un bit de l'ADC, il est impossible de rétablir la corrélation avec le signal d'origine et, à la suite de l'opération de codage-décodage, elles se transforment en bruit blanc. De plus, les bruits sont générés par des signaux évoluant rapidement avec une grande amplitude, ce que nous dirons beaucoup dans la musique pop.

Des approximations idéales à la vie réelle. Les problèmes des premiers lecteurs CD

Depuis le début de l'utilisation de la technologie numérique dans l'enregistrement sonore, il y a eu une course constante pour augmenter leur productivité et réduire les coûts. Les premiers lecteurs de CD avaient un seul DAC parallèle et deux circuits d'entrée, qui lui envoyaient alternativement des signaux du canal droit ou gauche. Les niveaux instantanés de signaux analogiques à la sortie du DAC ont été enregistrés à l'aide de circuits spéciaux pour le temps entre deux lectures et alimentés en alternance à des amplificateurs séparés des canaux droit et gauche. Cela a donné lieu à des distorsions supplémentaires, dont la valeur dépendait de la différence des niveaux sonores instantanés des canaux. Sous la pression des critiques des auidophiles, les fabricants ont été contraints de passer à un schéma avec des DAC séparés pour chaque canal.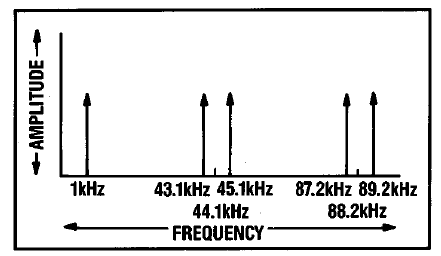

À la sortie du DAC, il y a un signal pas à pas, qui n'est pas trop similaire au signal source lisse, il y a des distorsions qui sont désagréables pour l'oreille. Pour simplifier, imaginons qu'une seule harmonique avec une fréquence de 1 KHz a été appliquée à l'entrée. L'opération de reconstruction du signal numérisé conduit en fait à l'apparition d'une distorsion d'intermodulation entre le signal d'origine et la fréquence d'échantillonnage - dans notre cas, 44,1 KHz. (Le mécanisme de l'apparition de la distorsion d'intermodulation et le programme éducatif sur les harmoniques, si nécessaire, peuvent être trouvés dans mon dernier article ).

Malgré le fait que les harmoniques parasites se trouvent à l'extérieur de l'oreille humaine, elles ont un effet néfaste sur le tractus d'amplification et il vaut mieux s'en débarrasser.

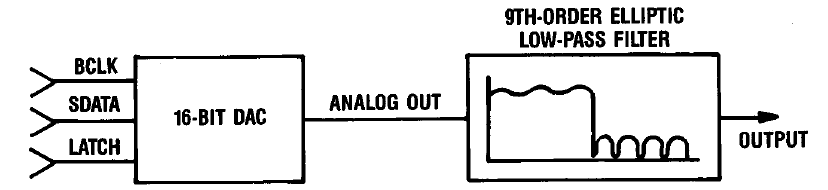Dans les premiers modèles d'équipement de reproduction de contenu numérique, des filtres étaient utilisés pour cela, qui avaient une caractéristique plate jusqu'à une fréquence de 20 kHz, puis une forte atténuation du niveau de 80 dB ou plus. Dans la terminologie anglaise, ces filtres sont appelés mur de briques, en russe ils sont parfois appelés par analogie «mur de briques». Le problème était que les filtres passe-bas analogiques d'ordre élevé sont très sensibles à la précision des valeurs des composants passifs qui les composent. La situation est encore plus compliquée par les évaluations requises, qui sont en ~~dehors de la plage standard~~et des exigences particulières pour la qualité de ces composants, qui sont nécessaires pour obtenir une contribution minimale à la distorsion du signal. En conséquence, le coût de ces filtres s'est avéré prohibitif, mais le plus triste est qu'ils ne pouvaient pas satisfaire les demandes des audiophiles, car ces filtres avaient de grandes distorsions de phase, en particulier aux bords de la plage reproduite. Par conséquent, le son des premières versions des lecteurs de CD, ~~malgré le coût élevé, les~~ audiophiles décrit comme « graveleux ».

Les filtres numériques se précipitent à la rescousse. Suréchantillonnage des doigts

Une étape importante vers l'amélioration de la qualité du son ~~et, surtout, sa disponibilité a~~ été l'introduction de la technologie de suréchantillonnage du signal, à laquelle cet article est consacré.

Afin de clarifier son essence, imaginons le processus de récupération du signal avec la fréquence GOST bien-aimée de 1 KHz. La figure A montre une série d'échantillons des composants du signal qui apparaissent à la sortie du DAC, et à droite, les composants spectraux du deuxième et du troisième ordre contenus dans le signal à la sortie du DAC. Vous pouvez voir que le signal n'est rien d'autre qu'un produit de distorsion d'intermodulation entre la tonalité initiale avec une fréquence de 1 KHz et la numérisation fréquente de 44,1 KHz.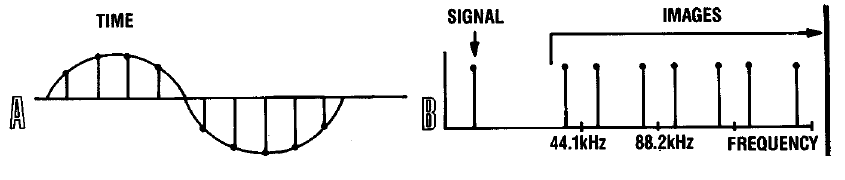

Nous allons augmenter le taux d'échantillonnage du signal quatre fois par une opération élémentaire - en ajoutant trois échantillons supplémentaires entre deux voisins, dont chacun a des valeurs nulles, comme le montre la figure C.En même temps, ajoutez les deux bits les moins significatifs dans chaque échantillon, en les remplissant également de zéros. Nous avons maintenant des valeurs d'échantillon de 18 bits. À la suite de cette opération, le spectre du signal n'a pas réellement changé, mais en fait, un changement fondamental s'est produit. Les harmoniques de second ordre provoqués par la fréquence d'échantillonnage font désormais partie du spectre du signal principal. Les harmoniques dérivées se sont déplacées au-dessus de la fréquence de 44,1 kHz. Ceci est illustré sur la figure D.

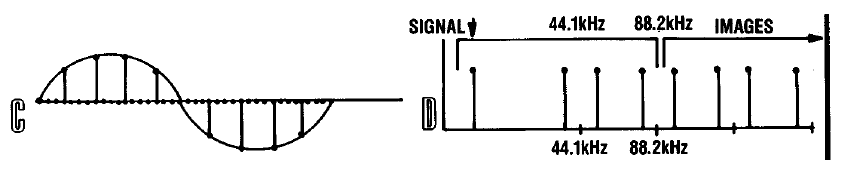Dans la région spectrale du signal principal, le filtrage numérique peut être appliqué avec succès, ce que nous ferons en utilisant un filtre numérique d'ordre élevé avec la réponse en fréquence indiquée sur la figure.Le F . Physiquement, nous obtenons des points intermédiaires supplémentaires entre les échantillons disponibles du signal, qui lissent les transitions entre les deux valeurs en raison de l'apparition de deux bits supplémentaires dans la représentation d'amplitude.

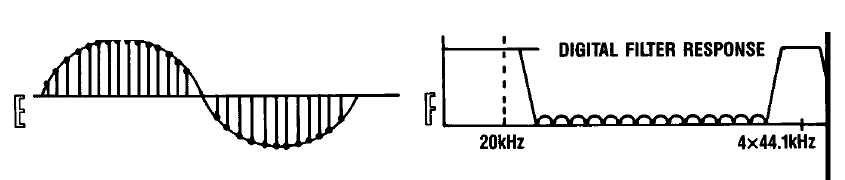Maintenant que le filtre numérique a fait tout le travail dur et sale, nous envoyons le signal résultant avec une fréquence d'échantillonnage de 44,1 * 4 = 176,4 KHz au DAC.

Il reste à ajouter une cerise à notre gâteau - faire passer le signal à travers le filtre analogique le plus simple du troisième ordre, qui résout parfaitement la suppression des harmoniques dans une plage donnée et n'introduit pas de distorsions de phase notables.

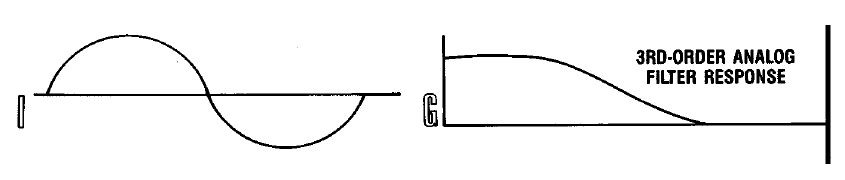Le résultat - le spectre du signal reçu est devenu beaucoup plus proche de l'original, les composants parasites qu'il contient sont considérablement atténués et les distorsions de phase sont minimisées en raison des capacités de filtrage numérique.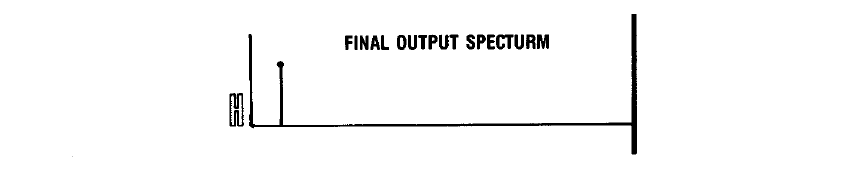

Implémentation matérielle

La figure montre l'implémentation matérielle de la solution décrite ci-dessus. Les opérations de rééchantillonnage et de filtrage numérique sont effectuées par la puce CXD1088Q fabriquée par SONY, l'un des progéniteurs du format CD audio. Un simple circuit logique démarre à son tour la conversion de deux DAC 18 bits AD1860 séparés.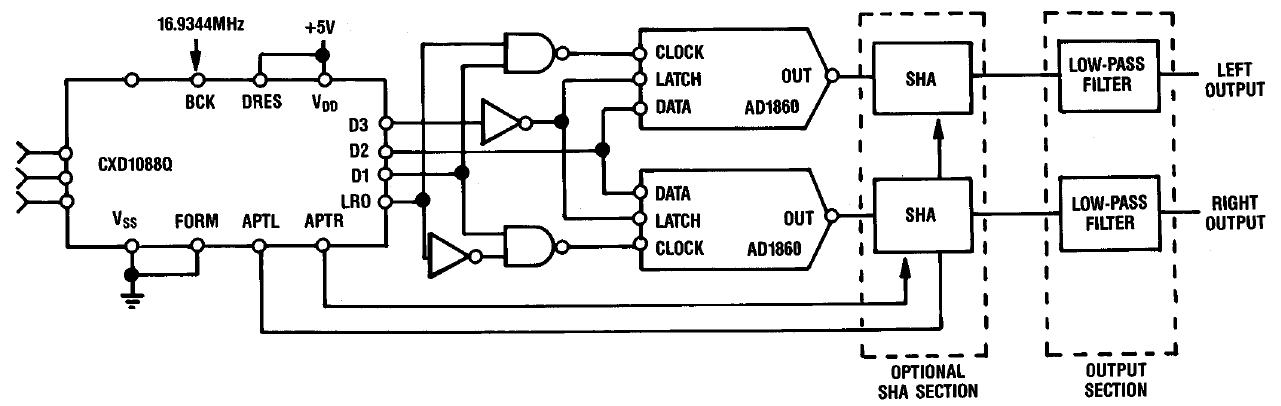

Quels avantages avons-nous retirés de nos tours numériques?

Réduction de la distorsion d'intermodulation
Faible distorsion de phase introduite par le filtre
Excellente suppression des harmoniques supérieures résultant du processus de conversion numérique-analogique, qui peut servir de source de distorsion d'intermodulation dans le chemin d'amplification
L'utilisation de convertisseurs numérique-analogique avec des profondeurs de bits plus élevées permet de réduire la non-linéarité de la conversion et le coefficient de distorsion harmonique car ils ont de meilleurs paramètres
, , .

, …

, . :

CD Hi Fi .

.

, .

, “ ”, ~~et pas seulement des~~ distorsions et élever leur prix au ciel.

Pour une comparaison plus détaillée du fonctionnement des filtres analogiques et numériques et des réponses aux questions typiques, voir l'article suivant

.

Lors de la préparation de la publication, les éléments de l'article CI du CAD: Combien de bits sont nécessaires? écrit par Robert Adams

Rééchantillonnage. Mur de briques numérique contre la théorie du complot. Conte de Noël pour les amateurs de son clair