Comment faire des papiers peints impossibles: une histoire de symétries interdites

Sur la gauche, un motif de papier peint avec une symétrie de rotation du sixième ordre autour de chacune des rosettes brun-vert. Sur la droite, un motif de papier peint avec une symétrie miroir par rapport aux lignes horizontales passant par chaque élément elliptique d'un ornement de vitrail.

À première vue, inventer un papier peint n'est pas plus difficile que d'accomplir les tâches d'un jardin d'enfants. Les concepteurs peuvent choisir n'importe quelle combinaison de couleurs et de formes pour la pièce d'origine, et simplement la multiplier dans deux directions. Selon le motif de la pièce initiale et le choix des directions, des symétries supplémentaires peuvent apparaître - par exemple, une symétrie du sixième ordre dans la première image ou une symétrie miroir dans la seconde. Les deux modèles ont été créés par le mathématicien Frank Farris de l'Université de Californie à Santa Clara.


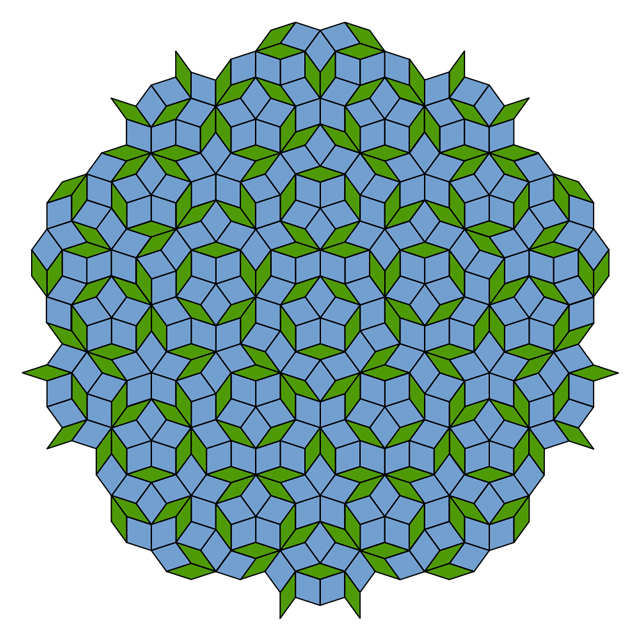Les carreaux de Penrose montrent de nombreux exemples de symétrie locale du cinquième ordre, mais ils n'ont pas de répétitions du motif. Lors du remplissage de grandes surfaces sur le plan, le rapport entre le nombre de carreaux larges et le nombre de carreaux étroits se rapproche du nombre d'or.

Mais, bien qu'il soit possible de créer des papiers peints avec des symétries de rotation des deuxième, troisième, quatrième ou sixième ordres, il est impossible de créer des papiers peints avec une symétrie du cinquième ordre [l'ordre montre combien de fois le motif s'alignera automatiquement pendant une rotation de 360 ​​° - env. trad.]. Cette restriction est connue des mathématiciens depuis près de 200 ans comme une «restriction cristallographique». La géométrie du pentagone interdit les motifs avec une symétrie du cinquième ordre. Il en va de même pour les commandes de sept ou plus.

Cependant, les motifs les plus intéressants, tels que les carreaux de Penrose, montrent une symétrie locale du cinquième ordre à de nombreux endroits et à différentes échelles, uniquement sans motifs répétitifs. En utilisant une méthode différente de l'approche de Penrose, Farris a freiné la géométrie inhabituelle de symétrie du cinquième ordre et a créé un nouvel ensemble d'images passionnantes - des pseudo-papiers peints qui ne semblent pas obéir, à première vue, à la contrainte cristallographique.


Fig. 4 La

4e figure ressemble à un contre-exemple de contrainte cristallographique, possédant une symétrie de rotation du cinquième ordre autour du point A, tandis que le motif peut être déplacé sur un plan dans les directions AB ou AC. En fait, Faris écrit dans son article pour la revue Notices of the American Mathematical Society que cette image n'est qu'un faux intelligent.

«Vous savez que la symétrie que vous observez est impossible», explique Stephen Kennedy du Carleton College au Minnesota.

La symétrie de rotation du cinquième ordre autour du point A semble être remplie. Mais si vous regardez attentivement, vous remarquerez que les roues autour des points B et C sont légèrement différentes de A. Si nous pouvions nous éloigner du motif pour voir plus de répétitions, alors les répétitions visibles du motif seraient de moins en moins comme un motif dans la région du point Et, même si des copies toujours plus convaincantes de A apparaissaient à d'autres endroits, comme sur la Fig. 5. Faris a montré que de telles illusions peuvent également être créées à plus grande échelle, en s'éloignant du modèle et en le répétant un certain nombre de fois - en particulier, le nombre de fois correspondant aux nombres de la série de Fibonacci (1, 1, 2, 3, 5, 8, 13, 21, ... où chaque nombre suivant est la somme des deux précédents), qui joue également un rôle dans la géométrie des carreaux Penrose.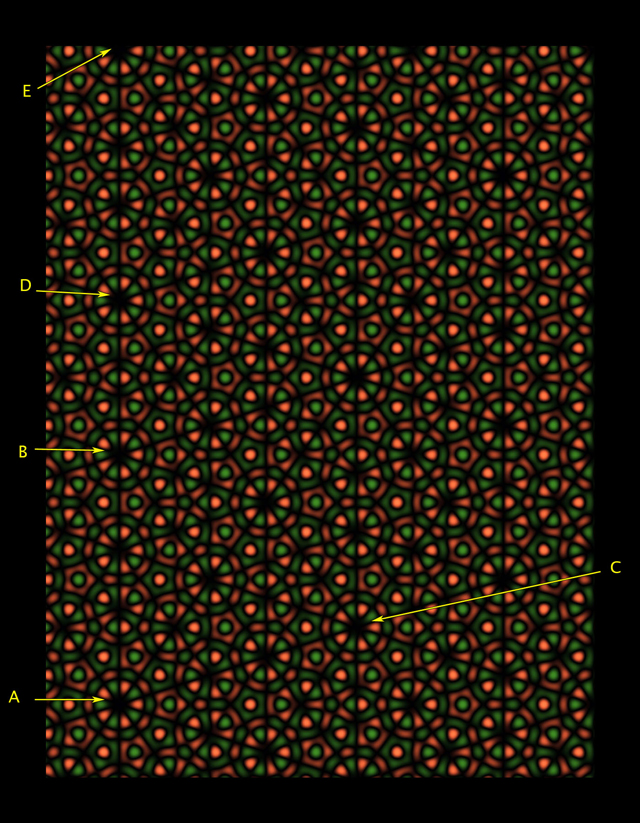


Fig. 5

«Par raison, nous comprenons qu'il s'agit d'une sorte de tromperie», explique Faris. Néanmoins, comme il l'écrit dans l'article, ces images «invitent nos yeux à les étudier et à apprécier des répétitions presque parfaites».

Faris a pensé à ces faux, changeant la technologie avec laquelle il a créé de vrais papiers peints avec une symétrie de rotation du 3ème ordre, comme dans la Fig. 6.

Pour créer une symétrie de troisième ordre, Faris a commencé à travailler dans l'espace tridimensionnel, qui a une rotation particulièrement naturelle, triant trois coordonnées spatiales et des points de rotation dans l'espace à 120 degrés autour de la diagonale. Faris a ensuite créé des motifs de papier peint en trois dimensions, superposant des sinusoïdes spécialement sélectionnés et les combinant avec une palette de couleurs présélectionnée. Les points étaient tachés en fonction de leur position sur les sinusoïdes superposées. Faris a ensuite sorti un papier peint plat, limitant cette couleur à un plan bidimensionnel perpendiculaire à l'axe de rotation de l'espace d'origine.

Cette approche douce et sinusoïdale de la création de motifs de papier peint est différente de la méthode traditionnelle de copier-coller, dit Kennedy. «C'est une toute nouvelle façon de créer des motifs symétriques.»


Fig. 6

La même procédure, réalisée dans un espace à cinq dimensions, semblait conduire à la création d'un motif avec une symétrie du cinquième ordre - si seulement nous ne savions pas que c'était impossible. Fait intéressant, pensa Faris, à quel moment ce système échoue-t-il?

Théoriquement, l'espace à cinq dimensions est possible, bien qu'il soit difficile à imaginer. Il a un analogue naturel de la symétrie de rotation du cinquième ordre, comme dans l'espace tridimensionnel - la symétrie du troisième. Dans l'espace à cinq dimensions, l'un des deux plans peut être sélectionné, chacun étant perpendiculaire à l'axe de rotation et à l'autre plan. Chacun d'eux peut pivoter autour d'un point de 72 ou 144 degrés. Il peut sembler difficile d'imaginer deux plans et une ligne droite perpendiculaires l'un à l'autre, mais en cinq dimensions, ils ont tous suffisamment d'espace.

Faris a compris le problème - si un plan perpendiculaire coupe avec précision l'espace tridimensionnel et contient des papiers peints infinis avec un nombre infini de points avec des coordonnées entières, alors deux plans perpendiculaires dans un espace cinq dimensions sont irrationnels et ne contiennent pas de points avec des coordonnées entières (à l'exception du point de référence) . Étant donné que le motif de papier peint créé à partir des sinusoïdes est répété par des décalages par des nombres entiers, ces plans n'héritent pas de motifs d'espaces d'ordre supérieur.

"C'est ainsi que la mouche apparaît dans la soupe", écrit Faris dans l'article.

Néanmoins, l'illusion de la structure du papier peint apparaît sur ces deux plans, grâce à la participation des soi-disant le nombre d'or, un nombre irrationnel qui décrit les directions de deux plans, et les nombres de Fibonacci.

Grâce à leurs relations, Faris a réussi à montrer que bien qu'il n'y ait pas de points avec des coordonnées entières sur deux plans, chacun d'eux est très proche de la diffusion infinie de points avec des coordonnées entières, dont les coordonnées sont des nombres de Fibonacci. Chaque fois que l'avion s'approche de l'un de ces points de Fibonacci, le motif ressemble presque au point de référence, ce qui crée l'illusion d'une copie exacte.



Faris a également compris comment combiner les couleurs et les motifs des photos de la nature avec les fonctions des vagues pour les inclure dans la conception des motifs, ce qui vous permet d'obtenir un grand nombre de "faux" fonds d'écran. Dans la figure ci-dessus, vous pouvez voir les branches d'arbres qui ont migré depuis la photo.

Source: https://habr.com/ru/post/fr400591/