Tautologies importantes en science. Partie 1. Physique

Savez-vous ce qu'est une tautologie logique? Tu le sais probablement. Et au cas où vous ne le sauriez pas, l'auteur va essayer d'expliquer ce concept maintenant. Nous ne commencerons pas à passer au langage sec et formel des mathématiques, nous ne serons pas des pédants sans âme comme Wikipedia, et nous dirons au figuré: une tautologie est une sorte d'Ouroboros se mordant la queue. Par exemple, "rien n'est quand il n'y a rien", ou, "des objets qui sont assez étroits et assez bas pour passer par cette porte le traverseront facilement" et similaires. De telles déclarations sont toujours vraies et, en gros, elles ne contiennent aucune nouvelle information. Étonnamment, un certain nombre de lois et de principes scientifiques importants contiennent des tautologies cachées, qui, cependant, ne nuisent pas à leur importance et à leur exactitude. Intéressant? Alors allez-y, sous la coupe!

L'empereur Sarlac Grant Scenticus III s'ennuyait. Très ennuyeux. Habituellement, quand il s'ennuyait, il jouait aux pierres (un jeu assez simple mais délicat, similaire en même temps à nos dames, reversi et Go ). Cependant, aujourd'hui, aucun des philosophes qui jouaient habituellement avec lui n'est venu. Il était assis à regarder fixement et regarda l'une des positions.

L'expérimentateur interne de Grant a décidé de compter le nombre de postes possibles. Laissons-le à cet endroit et faisons notre propre comptage.

Selon les règles, il est permis d'avoir jusqu'à 3 pierres sur une cellule. Il y a 6 pierres au total (3 pour chaque joueur). Nous ne prendrons pas en compte le nombre de tous les postes possibles. Il est beaucoup plus intéressant de calculer le nombre de façons dont vous pouvez définir une position. Mais d'abord, regardez le dessin.

Pour simplifier, nous considérons une seule cellule. La position ci-dessus peut être obtenue, par exemple, de trois manières différentes selon les pierres que nous avons disposées sur la planche: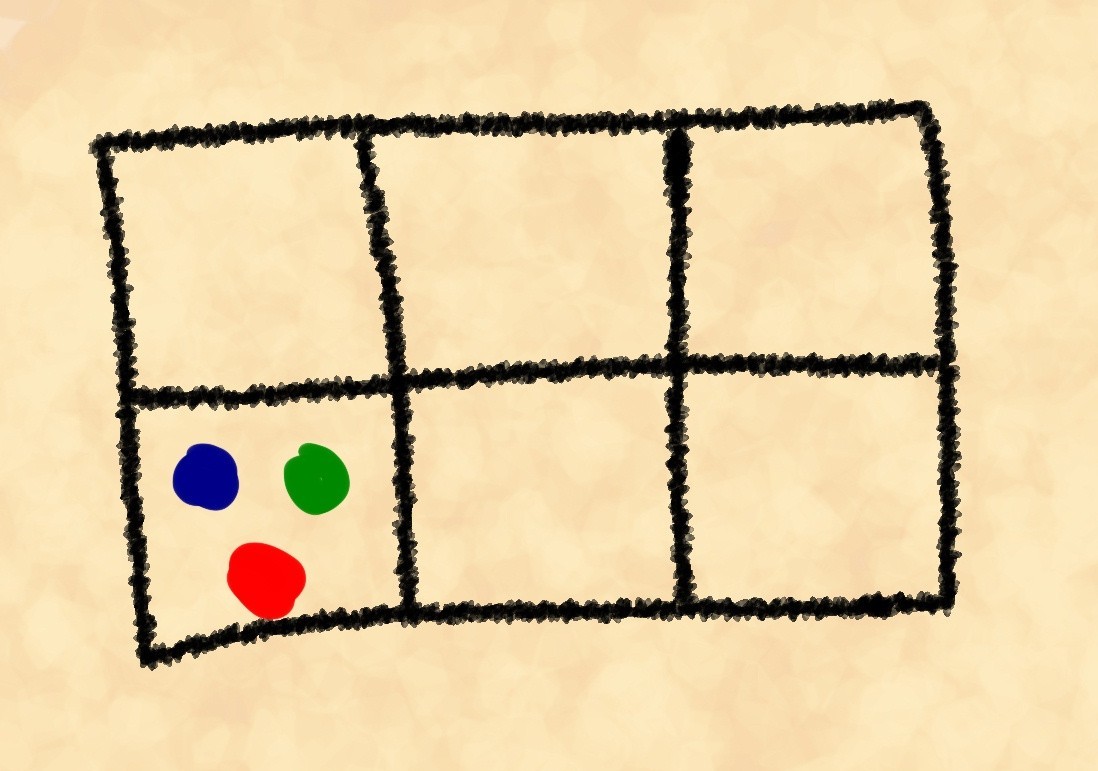

  

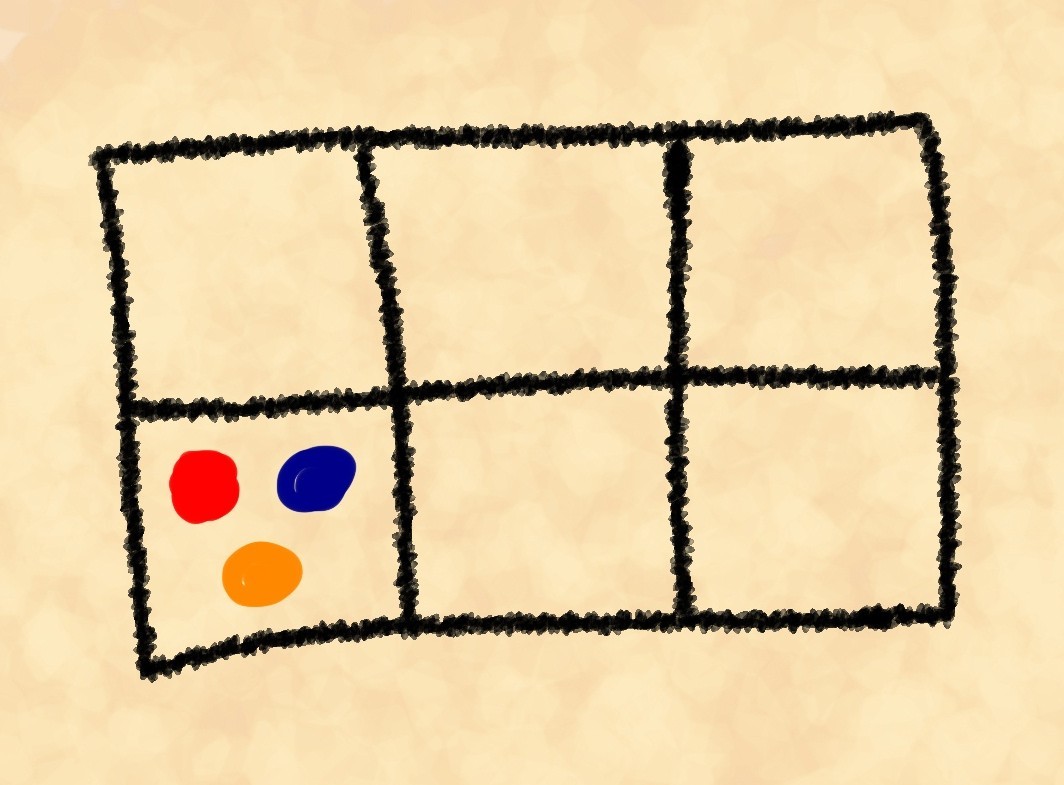Nous avons peint les pierres de manière conditionnelle afin de pouvoir les distinguer les unes des autres. De toute évidence, il existe bien plus de trois méthodes. Mais combien exactement? La première des trois pierres, nous pouvons choisir de six façons. Chacune de ces six options se poursuit avec un choix de la deuxième pierre parmi les cinq restantes et la dernière des quatre restantes. Nous avons$$$6\cdot5\cdot4=120$cependant, en même temps, nous avons permis des répétitions, par exemple, rouge-bleu-jaune, jaune-rouge-bleu et bleu-rouge-jaune sont le même "calcul".

Pour trouver le nombre de répétitions, nous trouvons de combien de façons nous pouvons poser trois pierres de la même couleur sur la planche. La première peut être l'une des trois pierres nécessaires, la seconde doit être l'une des deux restantes, la troisième sera la dernière pierre dont nous avons besoin:$$$3\cdot2\cdot1=6$.

En conséquence, nous avons 120/6 = 20 façons de disposer les pierres de la manière requise. Appelons ce nombre le poids de cette position. Bien sûr, cela n'a rien à voir avec le poids physique, juste ce nom est généralement accepté dans les statistiques.
Compliquons la tâche. Calculons les poids de ces positions:

  

si vous êtes trop paresseux pour comprendre tout ce calcul, sautez le paragraphe suivant.

Première position:

1. Nous avons étalé 2 pierres sur l'une des deux cellules de gauche: $$$2\cdot6\cdot5/2=30$
2. Dans la deuxième cellule, nous disposons deux pierres des 4 restantes: $$$4\cdot3/2=6$
3. Total que nous avons $$$30\cdot6/2=90$façons.

Pour les deuxième et troisième, nous avons respectivement $$$30\cdot4\cdot3/2=180$et $$$4\cdot6\cdot3\cdot5\cdot2\cdot4\cdot3/24=360$. La division dans tous les cas est effectuée afin de se débarrasser des répétitions.

Nous avons donc les poids suivants: 90 pour la première mise en page, 180 pour la seconde et 360 pour la troisième. Avez-vous remarqué que plus la position est rationalisée, moins son poids est important? Sa Majesté Grant l'a remarqué. Et maintenant, il va calculer le poids des positions de jeu réelles.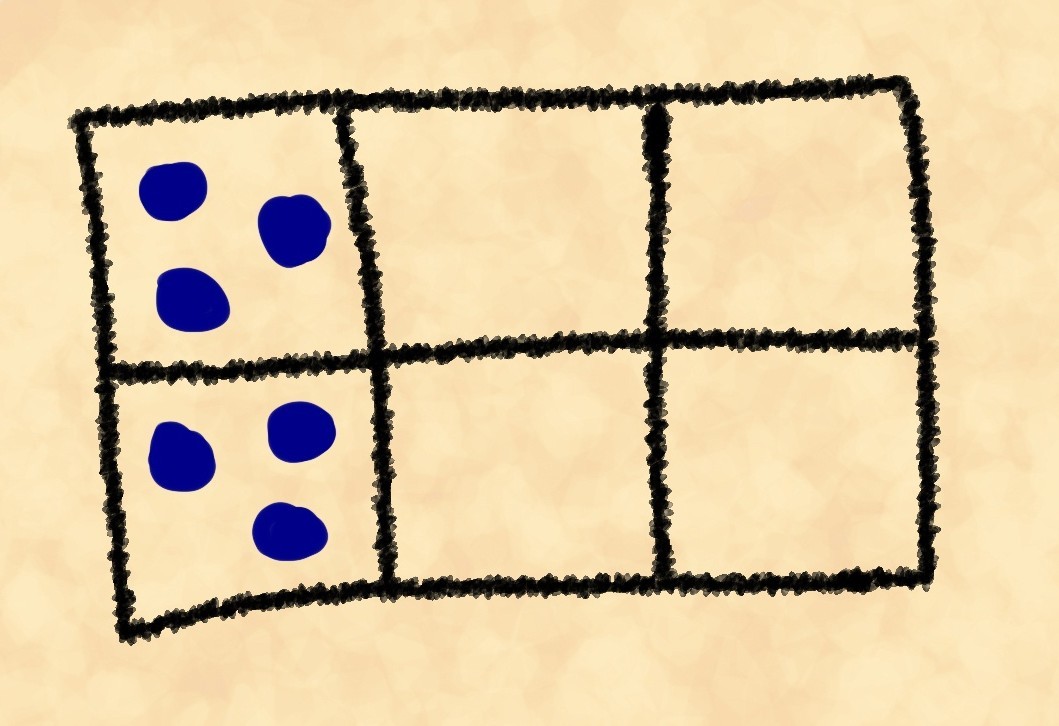

  

Il s'avère, respectivement, 90, 360 et 720. Cependant, ici sa patience s'arrête (comme, probablement, la vôtre). Il pousse la planche bouleversée, éparpillant les pierres au hasard, et remarque le philosophe Klofzus debout à la porte.

«Dites-moi, philosophe», demande-t-il avec une note de mécontentement, «pourquoi, quand je pousse la planche, les pierres volent autour d'elle de manière aléatoire et uniforme, et n'en tiennent pas trois dans une cage du bord?

Klofzius, en réponse à cela, sourit et dit:

"Pendant un certain temps, j'ai regardé vos calculs, suzerain, et vous pourriez probablement déjà répondre à cette question vous-même." Mais je dirai toujours - les pierres peuvent être commandées à partir du bord de la planche de quatre-vingt-dix façons différentes, et sept cent vingt peuvent être dispersées dans toutes les cellules. Pour les pierres, il y a beaucoup plus de façons d'être réparties uniformément sur la planche que collectées sur le bord.

Peut-être que nous quitterons ici Sarlak. Mais faites attention à l'explication de Klofzus: les pierres se dispersent sur le plateau car il y a beaucoup plus de façons de les disperser uniformément que de les disposer de manière ordonnée. Et la différence entre le nombre de méthodes (les poids des dispositions de pierres) est d'autant plus grande que la planche est grande et que le nombre de pierres est important. Pour une planche de 15 cellules (3 par 5) et 15 pierres, le poids d'une disposition entièrement ordonnée (3 pierres dans une cellule le long d'un bord) est d'environ 1,4 million (1401 400 si exactement), et pour un uniforme (une dans chaque cellule) - environ 1,3 quadrillion , c'est-à-dire près d'un million de fois plus. Par conséquent, dans ce cas, il est beaucoup plus facile d'obtenir un désordre que d'obtenir une commande. On se souvient involontairement d'une si merveilleuse déclaration: "Les œufs se brisent à chaque pas, mais personne n'a jamais vu,de sorte que les fragments d'un œuf cassé se rejoignent et deviennent un œuf entier. Et tout cela parce qu'il n'y a qu'une seule façon d'obtenir un œuf entier et une infinité de façons de se casser. »

Pour résumer la régularité que nous avons remarquée:

dans tout processus qui se déroule seul, sans influence extérieure supplémentaire, le résultat qui peut être atteint de la plus grande manière est le plus susceptible d'être réalisé.

Regardez de plus près, c'est une tautologie dans toute sa splendeur. Pour simplifier les choses, j'affirme simplement que «ce qui est plus facile à faire se produit plus souvent». Cependant, c'est aussi l'une des lois physiques les plus importantes. Beaucoup d'entre vous ont probablement déjà compris que nous parlons de la deuxième loi de la thermodynamique. Regardons une de ses formulations «officielles»: l'

entropie d'un système fermé ne peut pas diminuer.

Maintenant, cela ressemble moins à une tautologie, non? Mais quel genre de mot intelligent est l'entropie?

Imaginons que l'air remplisse une pièce. Il se compose d'un grand nombre de molécules. Si nous divisons mentalement la pièce en cellules, nous obtiendrons un analogue tridimensionnel du jeu de pierres sur une très grande planche avec un grand nombre de pierres. Dans ce cas, chaque position du jeu est appelée macrostate du système. Chacune des dispositions de pierres qui mettent en œuvre une position particulière est un micro-état . Nous prenons deux nombres: le nombre de tous les microstats qui réalisent ce macrostat et le nombre de tous les microstats possibles. Si nous divisons le premier en second, nous obtiendrons la probabilité de ce macrostat.

Définition du livre: l'entropie de l'état d'un système est le logarithme de la probabilité de cet état.

Nous le traduisons dans un langage que Grant comprend - l'entropie d'une position est le logarithme du poids d'une position donnée. Essayons de rendre cela encore plus clair: plus il y a de façons d'obtenir une position, plus il y a d'entropie.

Nous voyons maintenant que la formulation de livre du deuxième principe dit ceci: à partir d'une position en soi, seule une transition vers une position qui peut être obtenue dans plus ou avec le même nombre de chemins que le chemin initial peut se produire.

Essayons de le simplifier: si nous secouons le tableau, nous obtiendrons plus tôt une position plus facile à obtenir.

Il semble que nous soyons revenus à la tautologie. Cependant, même s'il s'agit d'une tautologie, le deuxième principe est l'une des lois physiques les plus importantes. De plus, c'est la seule loi de la physique qui nous dit que le temps doit s'écouler dans une certaine direction, ce qui fait la différence entre le passé et le futur.

Enfin, voyons quelques formulations supplémentaires du deuxième début:

• Postulat de Clausius: un processus circulaire est impossible, dont le seul résultat est le transfert de chaleur d'un corps moins chauffé à un corps plus chaud
• Le postulat de Thomson: Un processus circulaire est impossible, dont le seul résultat serait la production de travail en refroidissant le réservoir de chaleur.

Comme vous pouvez le voir, il n'y a plus de tautologie. Et aucun d'eux n'est évident. Cependant, il peut être démontré que ces deux formulations sont complètement équivalentes à la tautologie «il est très probable que quelque chose de plus probable se produira». Parfois, pour apprendre quelque chose de nouveau, nous devons d'abord prendre conscience de quelque chose d'évident.

Dans la partie suivante, nous considérerons une autre «tautologie scientifique» qui, à première vue, viole la deuxième loi de la thermodynamique.

Source: https://habr.com/ru/post/fr400803/