Moon Duchin, professeur agrégé de mathématiques et directeur du programme Science, technologie et société à l'Université Tufts (États-Unis)

Les partis politiques et les commissions électorales aux États-Unis, en Russie et dans d'autres pays «trichent» traditionnellement avec la taille et la forme des circonscriptions, essayant d'isoler la partie protestataire de l'électorat dans des réserves distinctes ou, au contraire, légèrement réparties dans les circonscriptions voisines. En raison de telles manipulations - jerrymandering - les quartiers acquièrent parfois des contours très bizarres. Mais tout est légal. Jusqu'à présent, il n'y a pas de législation normale avec des formules mathématiques décrivant la forme géométrique du quartier. Professeur agrégé de mathématiques à l'Université Tufts a l'intention de corriger cette lacune et propose plusieurs modèles mathématiques.

Le Jerrymandering est souvent utilisé dans les pays avec des élections parlementaires majoritaires et un système de partis fort. Afin que le nombre maximum de «leurs» députés puisse entrer au Parlement, les électeurs du parti d'opposition sont concentrés dans plusieurs circonscriptions, tandis que dans le reste, ils procurent un avantage modeste mais confiant à leur parti. C'est pourquoi les circonscriptions sont créées avec un nombre inégal d'électeurs, ainsi que des circonscriptions de forme territoriale bizarre.

Aux États-Unis, par exemple, le jerrymandering a été utilisé pour neutraliser les électeurs noirs afin que leurs candidats ne se rendent pas au Parlement (il y a eu des cas de discrimination positive lorsque ce sont des candidats noirs qui ont été promus de cette manière). Et en Russie en 2015, avant les élections législatives, une loi a été adoptée sur la coupe «pétale» des districts , dans laquelle de petits secteurs de grandes villes aux électeurs déloyaux rejoignent de grands territoires ruraux avec une population fidèle. En conséquence, le jerrymandering accomplit la même tâche - il bloque le passage de candidats «malveillants» au parlement dans la plupart des districts.

Par exemple, dans la région de Novossibirsk, les autorités ont divisé la population de la ville en quatre parties et attaché chacune d’elles au territoire de la région.


Districts électoraux de la région de Novossibirsk

Aux États-Unis, la situation avec le jerrymandering est encore pire, car dans la plupart des États, la réduction des circonscriptions est du ressort des parlements régionaux (c'est-à-dire en fait entre les mains du parti à majorité parlementaire). Par exemple, la région de Novossibirsk n'est même pas proche dans son degré d'idiotie de la répartition du Maryland à travers huit comtés.


Pièces du deuxième district Maryland


Pièces du troisième district Maryland

De plus, les constitutions des États ne fournissent généralement que des règles de base sur la forme des circonscriptions ou aucune règle. Il est généralement indiqué que le quartier doit être «compact», mais il s'agit clairement d'une déclaration large et subjective.

Pour changer la situation, Moon Dachin a créé une organisation d'experts composée de cinq membres, le Metric Geometry and Gerrymandering Group (MGGG), qui a ouvert une liste de diffusion pour commencer à discuter du problème du jerrymandering dans la communauté scientifique. Elle a décrit les objectifs de l'organisation dans une interview accordée à la revue Chronicle of Higher Education.

Qu'est-ce que la compacité?

Le professeur agrégé Dachin propose d'étudier la possibilité d'utiliser plusieurs concepts pour décrire la forme acceptable du quartier, c'est-à-dire de vérifier objectivement l'exigence de «compacité», qui est inscrite dans les constitutions des États.

Par exemple, vous pouvez considérer un paramètre tel que le score de Polsby-Popper , qui est calculé comme le rapport de l'aire d'un comté sur l'aire d'un cercle dont la longueur est égale au périmètre du comté.


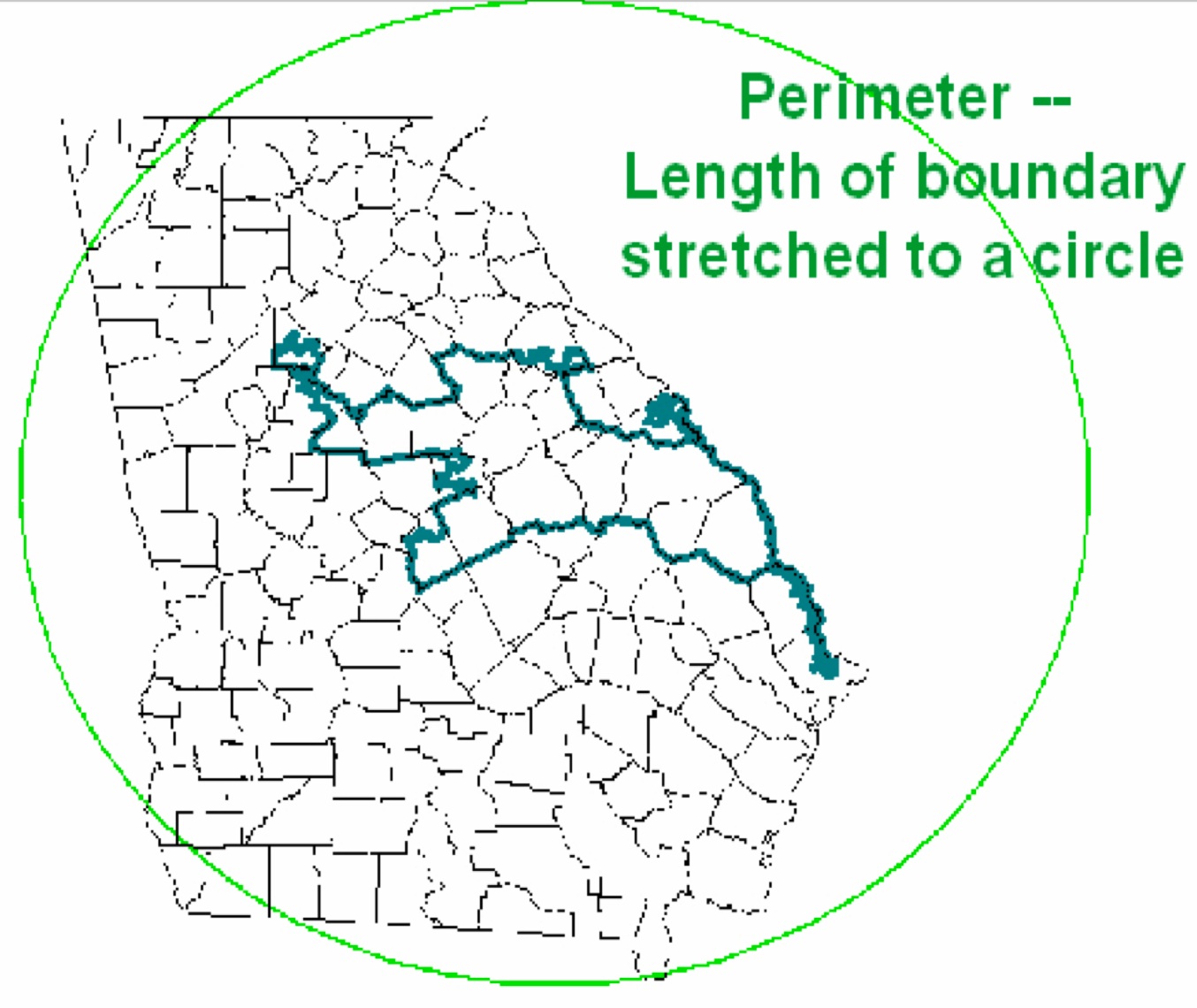Polsby Popper Score

Une autre option est un simple rapport de la superficie du district à la superficie du cercle dans le cercle circonscrit.


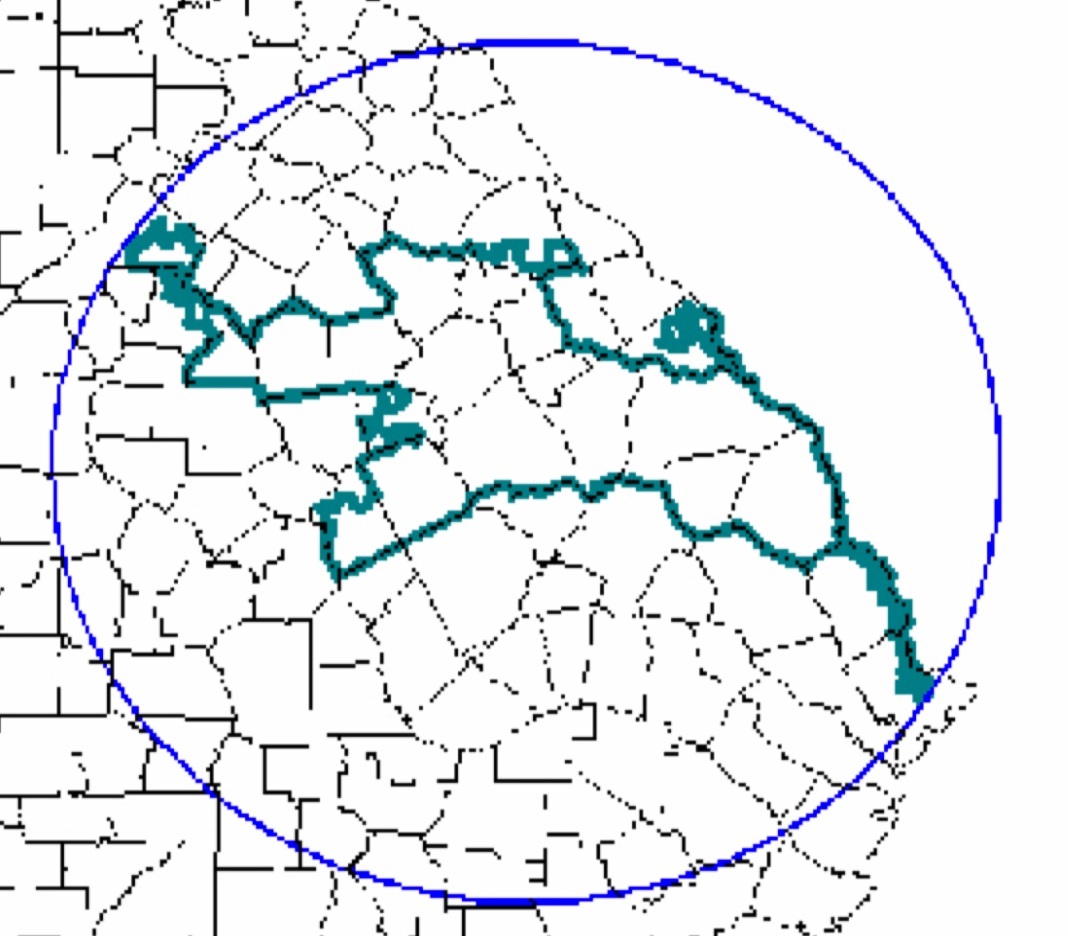Le rapport de l'aire du quartier à l'aire du cercle

Moon Dachin dit qu'il travaille actuellement sur des problèmes de géométrie métrique dans le cadre de la théorie géométrique des groupes . Il s'agit d'un domaine des mathématiques qui étudie les groupes générés de manière finie en utilisant les connexions entre leurs propriétés algébriques et les propriétés topologiques et géométriques des espaces sur lesquels ces groupes agissent, ou des groupes eux-mêmes, considérés comme des objets géométriques. Sur le site Web personnel de Danchin , vous pouvez trouver plusieurs travaux scientifiques dans ce domaine dans lesquels elle décrit un paramètre comme la distance moyenne entre tous les points d'une figure arbitraire (probablement, le paramètre doit encore être normalisé, par exemple, par le diamètre du même cercle circonscrit). Ce paramètre est tout à fait approprié en tant que caractéristique de compacité.

Une autre option pour évaluer la compacité, que les experts mentionnent en plaisantant , est le test interoculaire Grofman, qui a été proposé par le scientifique américain Bernie Grofman. Ce test vous permet de déterminer visuellement le niveau de gerrymandering en mesurant la largeur des yeux d'une personne, qui regarde la carte et évalue l'ampleur de la fraude. Soit dit en passant, le même test a déjà été proposé pour évaluer le porno "hardcore". Le fait est qu'il est difficile de formaliser de telles choses, mais quand vous le voyez, vous comprenez immédiatement (regardez à nouveau les comtés du Maryland).

Le professeur agrégé de l'Université Tufts est convaincu qu'avec l'aide des mathématiques, de nombreux problèmes sociaux peuvent être résolus. Mais la difficulté est que les politiciens ne peuvent souvent pas comprendre de simples concepts mathématiques. Par conséquent, il sera assez difficile de les convaincre d'introduire de telles formules dans les lois et la Constitution du pays. Après tout, ils doivent d'abord être compris. Moon Dachin donne un exemple du concept de manque d'efficacité , qui décrit Jerrymandering avec des exemples simples - un cas unique où un juge américain a compris les mathématiques et a dit qu'il les "aimait". Ce document mathématique a constitué la base de Whitford v. Nichol dans le Wisconsin. C'est ainsi que les concepts mathématiques doivent être expliqués et présentés aux juges, aux politiciens et à la société: aussi clair et convaincant que possible.