Comme nous le savons, tout corps flottant dans un liquide s'arrêtera tôt ou tard en raison des forces de frottement visqueux, si son mouvement n'est soutenu par aucun moteur. Mais il existe des liquides appelés superfluides dans lesquels la friction visqueuse est absente
(*) . L'exemple le plus célèbre d'un superfluide est l'
hélium liquide , refroidi à au moins 2,17 degrés au-dessus de la température zéro absolue.
Le mouvement avec une absence totale de viscosité se manifeste par de nombreux effets impressionnants: l'hélium superfluide s'écoule facilement à travers les fissures et les fissures les plus étroites, est capable de s'écouler sans fin dans un cercle
(**) et de s'échapper du récipient à travers le film liquide le plus mince adhérant à ses parois. Tous ces phénomènes sont des exemples d'effets quantiques à grande échelle.
Dans un
récent article théorique , la question a été posée: est-il possible de nager dans un liquide superfluide? En d'autres termes, un nageur hypothétique, bougeant ses bras et ses jambes, peut-il créer une force de traction qui lui permet d'accélérer ou de ralentir sans utiliser la force de la friction visqueuse?
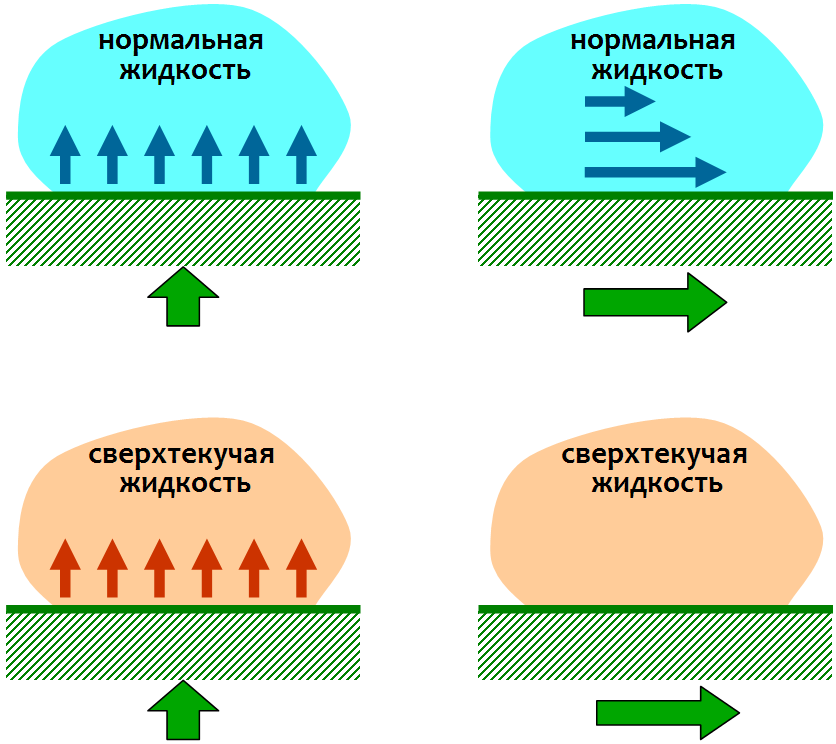
On peut réaliser la non-trivialité de la réponse à cette question en considérant le comportement des liquides normaux et superfluides en interaction avec les corps. Comme le montre la figure, un fluide normal peut être amené à se déplacer, à la fois en le poussant avec la surface d'un corps solide et en le traînant avec lui-même en raison des forces de friction visqueuses. Dans un liquide superfluide, celui-ci ne fonctionnera pas: il n'y a pas de frottement, et il ne peut être poussé, ce qui, comme nous le verrons, rend certaines méthodes de natation impossibles.
Pour analyser les principes généraux des phénomènes physiques, il est d'usage de considérer des modèles simples de «chevaux sphériques dans le vide». L'article en discussion ne fait pas exception: il considère les modèles de nageurs à deux et trois corps, qui sont deux et trois ellipsoïdes reliés par des «articulations». Les nageurs peuvent déplacer leurs ellipsoïdes, plier et déplier leurs articulations. Si le nageur parvient à s'éloigner du fluide environnant, il créera une traction et commencera à bouger.
Un nageur à deux corps ressemble à un mollusque bivalve et peut essayer de nager en changeant périodiquement l'angle entre ses ellipsoïdes comme un papillon battant des ailes. Cependant, les calculs montrent qu'il ne sera pas capable de nager: avec une vague, le nageur se déplace d'avant en arrière, mais en moyenne reste en place (
ici vous pouvez regarder une vidéo de ses mouvements simples).
Ci-dessus: profil de densité du liquide superfluide à différents moments. Les zones bleues à partir desquelles le fluide est expulsé sont des ellipsoïdes d'un nageur à deux corps.
Ci-dessous: coordonnées du nageur en fonction du temps.
Des parallèles peuvent être établis entre ces résultats et
le théorème du pétoncle de Purcell . Cet important théorème de la théorie de la natation dit qu'un mollusque bivalve, ouvrant et fermant lentement sa coquille dans un liquide visqueux, ne flottera nulle part tant que ses mouvements seront réversibles dans le temps. Ce dernier signifie que l'ouverture et la fermeture périodiques des volets de la coque ne changent pas leur apparence lorsque le temps commence dans la direction opposée (vous pouvez imaginer une vidéo qui regarde en arrière de la même manière qu'en lecture normale). Dans notre cas, le liquide n'a pas de viscosité, et ce n'est pas le théorème de Purcell qui fonctionne, mais son analogue pour un liquide superfluide.
Tiré d'un rapport d' Edward Purcell (prix Nobel de physique en 1952).La situation change lorsqu'un nageur à deux corps commence à balancer ses ellipsoïdes avec une plus grande fréquence. Si leur vitesse dépasse la vitesse du son dans un liquide, des ondes sonores et des tourbillons
(***) commencent à être émis. Ces excitations portent en elles une certaine impulsion qui, du fait du recul, fait bouger le nageur. La figure montre que dans ce cas, ses coordonnées fluctuent, mais diminuent globalement avec le temps, ce qui signifie que le nageur se déplace de droite à gauche. Après dix fluctuations (à droite de la ligne pointillée du graphique), le volet s'arrête et le nageur continue de se déplacer par inertie (
vidéo ).
Vous pouvez essayer un autre type de mouvement du nageur, lorsque ses ailes se ferment et s'écartent non seulement dans la bonne direction, mais alternativement dans deux directions. Ces mouvements symétriques sont similaires aux ailes battantes d'un papillon. Les calculs montrent que dans ce cas, de nombreux tourbillons quantifiés sont excités (ils sont visibles sur la figure sous forme de petits cercles), mais, en général, la natation n'est pas très efficace. La raison en est qu'environ le même nombre de tourbillons sont excités, se déplaçant à la fois vers la droite et vers la gauche, et les impulsions emportées par eux s'annulent en grande partie (
vidéo ).
Considérez maintenant un nageur à trois corps. Il a un avantage important sur celui à deux corps: il peut se tortiller, faire des mouvements serpentins qui ne passent pas en eux quand le temps passe. Cela signifie que le théorème de Purcell ne s'applique pas à lui, et il doit nager même avec des mouvements lents. Les calculs montrés sur la figure confirment cette conjecture: lors des mouvements de tortillement, le nageur se déplace avec confiance horizontalement, tout en se déplaçant légèrement verticalement (
vidéo ).
Ci-dessus: profil de densité du liquide superfluide à différents moments. Les zones bleues où le fluide est expulsé sont les ellipsoïdes du nageur à trois corps.
Ci-dessous: coordonnées horizontales (X) et verticales (Y) du nageur en fonction du temps.Quelle application peut être trouvée aux résultats obtenus? Il semblerait que la tâche de nager dans un superfluide ne soit pas particulièrement pertinente dans la pratique, mais il y a un domaine où elle peut être utile. Récemment, des expériences avec la condensation de Bose et la superfluidité des
gaz atomiques ultra -
froids se sont développées activement, avec lesquelles il existe de grands projets pour créer des simulateurs quantiques, des ordinateurs quantiques et une modélisation expérimentale des états exotiques de la matière. Dans de tels systèmes, il est possible de créer des caillots d'un gaz superfluide d'un type immergé dans un gaz superfluide d'un autre type. Si nous pouvons déformer la grappe selon nos besoins (et cela peut être fait à l'aide de faisceaux laser), il sera alors possible de faire nager cette grappe, à partir du gaz environnant. La figure montre les calculs démontrant cette possibilité: lorsque les changements de forme du bouquet ne sont pas réversibles dans le temps, il parvient vraiment à bouger (
vidéo ).
Ainsi, nous voyons qu'il est nécessaire de nager dans un fluide superflu à bon escient: le théorème de Purcell garantit que nous ne pouvons pas nager si nos mouvements de nos bras et de nos jambes coïncident avec nous lorsque nous jouons dans la direction opposée. Pour commencer à bouger, il faudra soit bouger plus vite que le son (ce qui est problématique), soit se tortiller comme un serpent, perturbant la réversibilité des mouvements dans le temps. Ces conclusions sont bien connues des micro-organismes flottant dans un liquide visqueux: pour contourner le théorème de Purcell, ils doivent utiliser des flagelles rotatifs en spirale, qui sont des analogues du nageur à trois corps considéré ici.
Selon l' article :
Hiroki Saito, Can We Swim in Superfluids?: Numerical Demonstration of Self-Propulsion in a Bose - Einstein Condensate, Journal of the Physical Society of Japan 84, 114001 (2015).(*) En fait, ce n'est pas entièrement vrai: tout véritable liquide superfluide peut être représenté comme une combinaison des composants «normaux» et superfluides ( modèle à deux fluides ), et le composant normal ralentira toujours le corps en mouvement. Cependant, cela n'empêche pas le composant superfluide de se déplacer complètement sans frottement.
(**) Dans la pratique, le flux circulaire d'hélium superfluide peut s'atténuer, mais pas à cause de la viscosité, mais à cause du processus mécanique quantique - glissement des tourbillons quantifiés. Aucune atténuation notable n'a été observée dans les expériences pendant 18 heures.
(***) Les tourbillons apparaissant dans un superfluide ne sont pas seulement des tourbillons comme de petites tornades, mais des excitations topologiques quantifiées . Contrairement aux tourbillons ordinaires, ils ne peuvent pas simplement disparaître en raison de l'atténuation progressive de l'écoulement.