Présentation
De nombreux articles populaires sont apparus qui parlent de l'intrication quantique. Les expériences avec l'intrication quantique sont assez spectaculaires, mais ne sont pas récompensées par des prix. Pourquoi des expériences aussi intéressantes pour le profane n'intéressent-elles pas les scientifiques? Des articles populaires parlent des propriétés étonnantes des paires de particules enchevêtrées - l'exposition à l'une entraîne un changement instantané de l'état de la seconde. Et ce qui se cache derrière le terme de «téléportation quantique», dont ils ont déjà commencé à dire que cela se passe à une vitesse supraluminique. Regardons tout cela du point de vue de la mécanique quantique normale.
Ce qui vient de la mécanique quantique
Selon le manuel classique de Landau et Lifshitz, les particules quantiques peuvent être dans deux types d'états - pures et mélangées. Si une particule n'interagit pas avec d'autres particules quantiques, elle est décrite par une fonction d'onde qui ne dépend que de ses coordonnées ou de ses impulsions - cet état est appelé pur. Dans ce cas, la fonction d'onde obéit à l'équation de Schrödinger. Une autre option est possible - la particule interagit avec d'autres particules quantiques. Dans ce cas, la fonction d'onde fait déjà référence à l'ensemble du système de particules en interaction et dépend de toutes leurs variables dynamiques. Si nous ne nous intéressons qu'à une seule particule, alors son état, comme Landau l'a montré il y a 90 ans, peut être décrit par un opérateur de matrice ou de densité. La matrice de densité obéit à une équation similaire à l'équation de Schrödinger
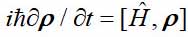
où
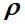
Est la matrice de densité,
H est l'opérateur de Hamilton et les parenthèses désignent le commutateur.
Landau l'a fait sortir. Toute quantité physique liée à une particule donnée peut être exprimée à travers une matrice de densité. Cette condition est appelée mixte. Si nous avons un système de particules en interaction, alors chacune des particules est dans un état mixte. Si les particules se sont dispersées sur de grandes distances et que l'interaction a disparu, leur état restera toujours mélangé. Si chacune de plusieurs particules est à l'état pur, alors la fonction d'onde d'un tel système est le produit des fonctions d'onde de chacune des particules (si les particules sont différentes. Pour des particules, bosons ou fermions identiques, il est nécessaire de faire une combinaison symétrique ou antisymétrique, voir [1], mais plus tard, l'identité des particules, des fermions et des bosons est déjà une théorie quantique relativiste.
Un état intriqué d'une paire de particules est un état dans lequel il existe une corrélation constante entre des quantités physiques liées à différentes particules. Un exemple simple et le plus courant est une certaine quantité physique totale, par exemple le spin total ou le moment angulaire d'une paire. Une paire de particules est à l'état pur, mais chacune des particules est à l'état mixte. Il peut sembler qu'un changement dans l'état d'une particule affectera immédiatement l'état d'une autre particule. Même s'ils se sont dispersés loin et n'interagissent pas, c'est ce qui est exprimé dans les articles populaires. Ce phénomène a déjà été qualifié de téléportation quantique. Certains journalistes analphabètes prétendent même que le changement se produit instantanément, c'est-à-dire qu'il se propage plus vite que la vitesse de la lumière.
Considérez cela du point de vue de la mécanique quantique: premièrement, toute action ou mesure qui modifie le spin ou le moment angulaire d'une seule particule viole immédiatement la loi de conservation de la caractéristique totale. L'opérateur correspondant ne peut pas commuter avec un spin complet ou un moment angulaire complet. Ainsi, l'intrication initiale de l'état d'une paire de particules est violée. Le spin ou le moment de la seconde particule ne peut plus être associé sans ambiguïté à celui de la première. Vous pouvez considérer ce problème de l'autre côté. Après disparition de l'interaction entre les particules, l'évolution de la matrice de densité de chacune des particules est décrite par sa propre équation, dans laquelle les variables dynamiques des autres particules ne sont pas incluses. Par conséquent, l'exposition à une particule ne changera pas la matrice de densité en une autre.
Il existe même le théorème d'Eberhard [2], qui prétend que l'influence mutuelle de deux particules ne peut pas être détectée par des mesures. Soit un système quantique, qui est décrit par une matrice de densité. Et que ce système se compose de deux sous-systèmes A et B. Le théorème d'Eberhard déclare qu'aucune mesure des observables liés uniquement au sous-système A n'affecte le résultat de la mesure des observables qui ne sont liés qu'au sous-système B. Cependant, la preuve du théorème utilise l'hypothèse de réduction des vagues une fonction qui n'a été prouvée ni théoriquement ni expérimentalement. Mais toutes ces considérations sont faites dans le cadre de la mécanique quantique non relativiste et concernent différentes particules non identiques.
Ces considérations ne fonctionnent pas dans la théorie relativiste dans le cas d'une paire de particules identiques. Permettez-moi de vous rappeler une fois de plus que l'identité ou l'indiscernabilité des particules vient de la mécanique quantique relativiste, où le nombre de particules n'est pas préservé. Cependant, pour les particules lentes, nous pouvons utiliser un appareil plus simple de mécanique quantique non relativiste, prenant simplement en compte l'indiscernabilité des particules. La fonction d'onde de la paire doit alors être symétrique (pour les bosons) ou antisymétrique (pour les fermions) par rapport à la permutation des particules. Une telle exigence se pose dans la théorie relativiste, indépendamment des vitesses des particules. C'est cette exigence qui conduit à des corrélations à longue distance d'une paire de particules identiques. En principe, un proton avec un électron peut également être dans un état intriqué. Cependant, s'ils se dispersent par plusieurs dizaines d'angströms, l'interaction avec les champs électromagnétiques et d'autres particules détruira cet état. L'interaction d'échange (comme ce phénomène est appelé) agit à des distances macroscopiques, comme le montrent les expériences. Une paire de particules, même dispersées par des mètres, reste indiscernable. Si vous prenez une mesure, vous ne savez pas exactement à quelle particule appartient la valeur mesurée. Vous prenez des mesures avec une paire de particules en même temps. Par conséquent, toutes les expériences spectaculaires ont été réalisées avec exactement les mêmes particules - électrons et photons. À strictement parler, ce n'est pas tout à fait l'état déroutant qui est considéré dans le cadre de la mécanique quantique non relativiste, mais quelque chose de similaire.
Prenons le cas le plus simple - une paire de particules identiques sans interaction. Si les vitesses sont faibles, nous pouvons utiliser la mécanique quantique non relativiste, en tenant compte de la symétrie de la fonction d'onde par rapport à la permutation des particules. Soit la fonction d'onde de la première particule
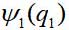
, la deuxième particule -
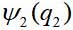
où
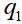
et
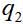
- les variables dynamiques des première et deuxième particules, dans le cas le plus simple - juste les coordonnées. Ensuite, la fonction d'onde de la paire
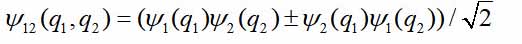
Les signes + et - se réfèrent aux bosons et fermions. Supposons que les particules soient éloignées les unes des autres. Alors

localisés dans les zones éloignées 1 et 2, respectivement, c'est-à-dire qu'en dehors de ces zones, ils sont petits. Essayons de calculer la valeur moyenne d'une variable de la première particule, par exemple la coordonnée. Pour simplifier, nous pouvons imaginer que seules les coordonnées sont incluses dans les fonctions d'onde. Il s'avère que la valeur moyenne des coordonnées de la particule 1 se situe entre les régions 1 et 2, et qu'elle coïncide avec la valeur moyenne de la particule 2. C'est en fait naturel - les particules sont indiscernables, nous ne pouvons pas savoir quelle particule les coordonnées sont mesurées. En général, toutes les valeurs moyennes des particules 1 et 2 seront les mêmes. Cela signifie qu'en déplaçant la région de localisation de la particule 1 (par exemple, la particule est localisée à l'intérieur du défaut du réseau cristallin, et nous déplaçons le cristal entier), nous agissons sur la particule 2, bien que les particules n'interagissent pas dans le sens habituel - à travers un champ électromagnétique, par exemple. Ceci est un exemple simple d'enchevêtrement relativiste.
Aucun transfert instantané d'informations en raison de ces corrélations entre les deux particules ne se produit. L'appareil de la théorie quantique relativiste a été initialement construit pour que les événements dans l'espace-temps sur les côtés opposés du cône de lumière ne puissent pas s'influencer mutuellement. Autrement dit, aucun signal, aucune influence ou perturbation ne peut se propager plus rapidement que la lumière. Les deux particules sont en fait un état d'un champ, par exemple, électron-positon. En agissant sur le champ en un point (sur la particule 1), nous créons une perturbation qui se propage comme des vagues d'eau. En mécanique quantique non relativiste, la vitesse de la lumière est considérée comme infiniment grande, ce qui crée l'illusion d'un changement instantané.
La situation où les particules espacées sur de longues distances restent couplées par paires semble paradoxale en raison des idées classiques sur les particules. Nous devons nous rappeler qu'en réalité, il n'y a pas de particules, mais des champs. Ce que nous représentons comme particules est simplement l'état de ces champs. L'idée classique des particules est totalement inadaptée dans le micromonde. Des questions se posent immédiatement sur la taille, la forme, le matériau et la structure des particules élémentaires. En fait, des situations paradoxales pour la pensée classique surviennent avec une seule particule. Par exemple, dans l'expérience Stern-Gerlach, un atome d'hydrogène vole à travers un champ magnétique inhomogène dirigé perpendiculairement à la vitesse. Le spin du noyau peut être négligé en raison de la petitesse du magnéton nucléaire; que le spin de l'électron soit initialement dirigé le long de la vitesse.
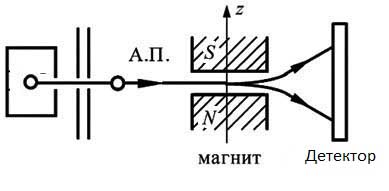
L'évolution de la fonction d'onde atomique est facile à calculer. Le paquet d'onde localisé initial est divisé en deux identiques, volant symétriquement à un angle par rapport à la direction d'origine. C'est-à-dire un atome, une particule lourde, généralement considérée comme classique avec une trajectoire classique, divisée en deux paquets d'ondes qui peuvent se disperser à des distances complètement macroscopiques. En même temps, je note - il résulte du calcul que même une expérience idéale de Stern-Gerlach n'est pas en mesure de mesurer le spin des particules.
Si le détecteur lie un atome d'hydrogène, par exemple, chimiquement, alors les «moitiés» - deux paquets d'ondes diffusées, sont assemblés en un seul. Comment une telle localisation de la particule tachée se produit est une théorie existant séparément dans laquelle je ne comprends pas. Les personnes intéressées peuvent trouver une abondante littérature sur ce sujet.
Conclusion
La question se pose: quel est l'intérêt de nombreuses expériences pour démontrer les corrélations entre particules à grande distance? En plus de confirmer la mécanique quantique, dont aucun physicien normal ne doute depuis longtemps, il s'agit d'une démonstration spectaculaire qui impressionne les fonctionnaires publics et amateurs qui allouent des fonds à la science (par exemple, Gazprombank parraine le développement de lignes de communication quantiques). Pour la physique, ces démonstrations coûteuses ne donnent rien, bien qu'elles permettent le développement de techniques expérimentales.
Littérature1. Landau, L. D., Lifshits, E. M. Mécanique quantique (théorie non relativiste). - 3e édition, révisée et complétée. - M.: Nauka, 1974.- 752 p. - («Physique théorique», Volume III).
2. Eberhard, PH, «Le théorème de Bell et les différents concepts de non-localité», Nuovo Cimento 46B, 392-419 (1978)