«Il y a deux balles identiques à la même température. L'un d'eux repose sur une surface horizontale, l'autre est suspendu à un fil. Les deux balles rapportent la même quantité de chaleur. Les balles seront-elles les mêmes après cela ou non? (Tout type de perte de chaleur peut être négligé.) "

Un tel problème peut parfois être trouvé dans les olympiades de physique et de médias sociaux . La réponse généralement acceptée est intuitive: en raison de la consommation d'énergie pour la dilatation thermique en présence de gravité, une boule reposant sur une surface horizontale sera plus froide que suspendue à un fil. Un article récent a montré que cette réponse est incorrecte. En fait, le résultat sera inverse: la balle couchée sera plus chaude que la balle suspendue. Nous comprendrons pourquoi la méthode traditionnelle de résolution de ce problème conduit à une mauvaise réponse, et pourquoi l'intuition dans ce cas nous déprime.

Solution traditionnelle et son problème

La solution traditionnelle est basée sur le raisonnement suivant. Les deux balles se dilateront pendant le chauffage, de ce fait le centre de masse de la balle reposant sur une surface horizontale augmentera légèrement et le centre de masse de la balle suspendue baissera. En conséquence, la balle couchée chauffe plus faible, car une partie de la chaleur qui lui est transférée sera dépensée lors de sa montée, et la balle suspendue se réchauffera davantage en raison du travail de gravité supplémentaire lorsqu'elle est abaissée.


Raisonnement utilisé dans la solution traditionnelle: en raison de la dilatation thermique, la balle posée sur la table se lève et la balle accrochée au fil est abaissée.

La réponse peut être exprimée par une formule simple pour la différence de température située ( $$ ) et suspendu ( $$ ) balles:

$$

où $$ , $$ et $$ - masse, rayon et capacité thermique des billes, $$ - la quantité de chaleur qui leur est transférée, $$ - accélération de la gravité, $$ Est le coefficient de dilatation thermique linéaire du matériau des billes, que nous considérons comme suffisamment petit. Comme vu $$ - la balle couchée sera plus froide.

Il semblerait que dans cette décision tout soit logique. La «première déglutition», démontrant que quelque chose ne va pas ici, est une tentative mentale de créer un moteur thermique sur la base du ballon.

La machine peut fonctionner comme suit: premièrement, la balle repose sur la table, où nous la chauffons, à cause de laquelle son centre de masse s'élève. Ensuite, nous fixons la balle sur le fil accroché sur le dessus et retirons soigneusement la table afin que la hauteur de la balle ne change pas. Enfin, nous refroidissons la balle à sa température initiale, de sorte que la balle est comprimée et que son centre de masse augmente. En bout de ligne: la partie de la chaleur que nous avons transférée à la balle lorsqu'elle a été chauffée s'est transformée en travail mécanique pour la relever, et ce cycle peut être répété à l'infini.


Le cycle de fonctionnement d'un moteur thermique à bille: après chauffage et refroidissement, la bille s'est élevée, ce qui signifie que nous avons transformé une partie de la chaleur en travail mécanique.

Le problème ici est qu'en augmentant le rayon de la balle, le rendement (efficacité) d'une telle machine peut être rendu arbitrairement proche de 100%. Cela contredit la deuxième loi de la thermodynamique , selon laquelle l'efficacité d'un moteur thermique ne peut pas dépasser l'efficacité du cycle Carnot aux mêmes températures de l'appareil de chauffage et du réfrigérateur.

Quelle est la question?

Pourquoi la solution traditionnelle au problème est-elle mauvaise? Ici, il est nécessaire de tenir compte du fait que la balle posée sur la table dès le début, avant qu'elle ne soit chauffée, sera légèrement aplatie par gravité et que la balle suspendue sera légèrement étirée. Cela affectera négativement l'efficacité du moteur thermique décrit ci-dessus: pendant la suspension, le ballon s'abaissera légèrement, de ce fait l'efficacité diminuera et ne dépassera plus l'efficacité du cycle Carnot.


L'effet de la gravité sur les balles: la balle posée sur la table est aplatie et celle accrochée au fil est tendue.

Comment cela se manifestera-t-il lors de l'examen du problème d'origine? Il s'avère que la compression ou l'étirement d'un matériau modifie sa capacité thermique: dans le cas d'un matériau comprimé, le chauffage à la même température nécessitera moins de chaleur que dans le cas d'un matériau étiré. Par conséquent:

• Lorsque la balle posée sur la table est chauffée, une partie de la chaleur ira à sa montée due à la dilatation thermique; mais, parallèlement à cela, le chauffage du matériau de balle lui-même sera plus facile et nécessitera moins de chaleur.
• Lorsqu'une boule suspendue à un fil est chauffée, le travail de gravité lorsqu'elle est abaissée s'ajoute à la chaleur qui lui est transférée; mais, parallèlement à cela, le chauffage du matériau de balle lui-même prendra plus de temps et nécessitera plus de chaleur.

Dans la solution traditionnelle, seuls les facteurs indiqués par des flèches blanches sont pris en compte. Ignorer les facteurs indiqués par les flèches noires conduit à une réponse erronée.

Comme nous pouvons le voir, dans les deux cas, il y a des facteurs qui fonctionnent à la fois en faveur d'une seule option de réponse (une balle couchée peut se révéler plus froide qu'une balle suspendue) et dans la direction opposée (une balle couchée peut se révéler plus chaude qu'une balle suspendue). Lequel domine?

Il semblerait que l'effet de la modification de la capacité calorifique d'un matériau lors de la compression ou de la traction, même s'il existe, devrait être très faible, et il peut être négligé, comme cela se fait dans la solution traditionnelle du problème. Mais ce n'est pas le cas. Cet effet est du même ordre de petitesse que l'expansion thermique elle-même, car ces deux effets découlent de l'anharmonicité des forces interatomiques. La prise en compte de l'un de ces effets dans la solution traditionnelle combinée à l'ignorance de l'autre est incohérente et conduit à une réponse erronée.

L'article montre qu'avec la bonne solution au problème, la différence de température des billes après leur avoir transféré la même quantité de chaleur est égale à:

$$

où $$ - la température absolue des billes, $$ - le taux de variation du coefficient de dilatation thermique du matériau des billes avec un changement de sa température.

Par rapport au résultat de la solution traditionnelle, la différence de température est:

• Le signe opposé, car pour la plupart des matériaux la valeur $$ est positif, donc tout le côté droit de l'égalité est également positif, et $$ .
• Beaucoup plus petit en valeur absolue, car ici au lieu d'une petite valeur apparaissent des valeurs encore plus petites $$ et $$ .

Ainsi, les deux effets discutés ci-dessus s'annulent presque complètement, mais le second d'entre eux (changement de capacité thermique lors de la compression ou de la traction) est légèrement plus fort que le premier (dilatation thermique).

Anharmonicité des forces interatomiques

Les auteurs de l'article effectuent un examen assez rigoureux du problème, mais, malheureusement, ne fournissent pas d'explication claire sur la façon dont la compensation presque complète des deux effets se produit, j'ai donc dû traiter ce problème moi-même.

La figure montre une dépendance typique de l'énergie potentielle de l'interaction atomique de la distance entre eux. La force agissant sur les atomes est dirigée vers une diminution de l'énergie potentielle; par conséquent, les atomes se repoussent fortement à de petites distances et sont faiblement attirés à de grandes distances. À une certaine distance $$ l'énergie potentielle atteint un minimum. Le désir des atomes à cette distance la plus avantageuse sur le plan énergétique est la raison de leur liaison aux molécules, aux liquides et aux solides.


Voyons maintenant d'où vient l'expansion thermique des matériaux. Avec un mouvement thermique chaotique, la distance entre les atomes n'est plus strictement égale $$ et fluctue près de cette valeur. Le lien entre atomes a la propriété d'un harmonisme: il se comporte comme un ressort asymétrique, plus facile à étirer qu'à comprimer. En conséquence, pendant le mouvement thermique, la liaison est étirée la plupart du temps, plutôt que compressée, de sorte que la distance moyenne $$ entre les atomes devient plus que $$ . Avec l'augmentation de la température, cet effet s'intensifie, les distances entre les atomes augmentent et le matériau se dilate.


La raison de l'expansion thermique des matériaux: pendant le mouvement thermique, la distance moyenne entre les atomes augmente en raison de l'anharmonicité des forces d'interaction interatomiques.

Que se passe-t-il lorsque le matériau est comprimé ou étiré, comme dans le cas de balles aplaties ou étirées? Lorsqu'un matériau est comprimé, une force externe diminue la distance moyenne entre les atomes et, lorsqu'elle est étirée, elle augmente.


Sous compression, la distance d'équilibre entre les atomes diminue, tandis que sous tension, elle augmente.

Nous sommes maintenant prêts à comprendre comment la compression et la tension d'un matériau affectent sa capacité thermique. Imaginez que nous avons pressé le matériau, de sorte que la distance entre les atomes pendant le mouvement thermique oscille maintenant près de la position d'équilibre décalée vers la gauche. Dans ce cas, l'anharmonisme n'a pas disparu, par conséquent, comme auparavant, lorsqu'il est chauffé, la distance moyenne entre les atomes augmentera. Mais en même temps, nous reculerons vers le minimum d'énergie potentielle, ce qui signifie que l'énergie du matériau diminuera encore! Cela explique la diminution de la capacité thermique du matériau lors de la compression: la dilatation thermique entraîne une petite diminution supplémentaire de l'énergie des interactions interatomiques, par conséquent, moins d'énergie est requise pour chauffer le matériau.



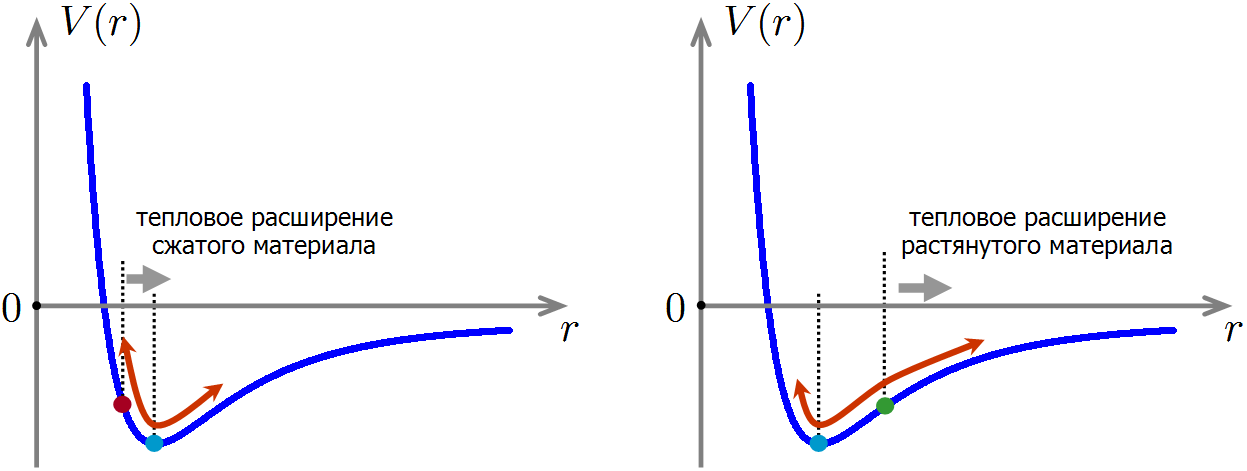
Si le matériau est étiré, la situation est inverse: avec l'expansion thermique, l'énergie d'interaction des atomes croîtra plus rapidement que dans un matériau non étiré. Par conséquent, pour chauffer le matériau étiré à la même température, un peu plus d'énergie est requise que sans étirement, ce qui signifie que la capacité thermique du matériau étiré sera plus élevée.

Ainsi, sur l'exemple du problème des olympiades, qui pendant de nombreuses décennies a été résolu (et, peut-être, continue d'être résolu) par erreur, nous voyons que la physique réelle contredit parfois notre intuition. Par conséquent, il est si important lors de la résolution de problèmes d'utiliser soigneusement l'appareil mathématique, non limité au raisonnement superficiel.

Selon l' article :

Giacomo De Palma, Mattia C. Sormani, Effet contre-intuitif de la gravité sur la capacité thermique d'une sphère solide: réexamen d'un problème bien connu, American Journal of Physics 83, 723 (2015).
Préimpression publique de l'article: arxiv.org/pdf/1502.01337