Préface à la première partie
La modélisation des turbines à vapeur est une tâche quotidienne pour des centaines de personnes dans notre pays. Au lieu du mot modèle, il est courant de dire une caractéristique de dépense . Les caractéristiques de consommation des turbines à vapeur sont utilisées pour résoudre des problèmes tels que le calcul de la consommation spécifique de combustible équivalent pour l'électricité et la chaleur produites par les centrales thermiques; optimisation du CHP; planification et maintenance des modes de centrales thermiques.
J'ai développé une nouvelle caractéristique d'écoulement d'une turbine à vapeur - une caractéristique d'écoulement linéarisée d'une turbine à vapeur. La caractéristique d'écoulement développée est pratique et efficace pour résoudre ces problèmes. Cependant, pour le moment, il n'est décrit que dans deux articles scientifiques:
- Optimisation du fonctionnement des centrales thermiques dans les conditions du marché de gros de l'énergie électrique et de la capacité de la Russie ;
- Méthodes de calcul pour déterminer la consommation spécifique de combustible équivalent des centrales thermiques pour l'énergie électrique et thermique fournie en mode de production combinée .
Et maintenant dans mon blog je voudrais:
1. Les données source
Les données initiales pour construire une caractéristique d'écoulement linéarisée peuvent être
- valeurs réelles de puissance Q 0 , N, Q p , Q t mesurées pendant le fonctionnement de la turbine à vapeur,
- nomogrammes q t bruts issus de la documentation normative et technique.
Bien entendu, les valeurs instantanées réelles de Q
0 , N, Q
p , Q
t sont des données source idéales. La collecte de ces données prend du temps.
Dans les cas où les valeurs réelles de Q 0 , N, Q p , Q t ne sont pas disponibles, vous pouvez traiter les nomogrammes q t brut. Ils ont à leur tour été obtenus sur la base de mesures. En savoir plus sur les tests de turbines dans VM Gornstein et d'autres méthodes d'optimisation des modes des systèmes énergétiques .
2. L'algorithme de construction d'un flux linéarisé
L'algorithme de construction se compose de trois étapes.
- Traduction des nomogrammes ou des résultats de mesure dans une vue tabulaire.
- Linéarisation de la caractéristique d'écoulement d'une turbine à vapeur.
- Détermination des limites de la plage de contrôle de la turbine à vapeur.
Lorsque vous travaillez avec des nomogrammes q t brut, la première étape est rapide. Ce travail s'appelle la numérisation . La numérisation de 9 nomogrammes pour l'exemple actuel m'a pris environ 40 minutes.
Les deuxième et troisième étapes nécessitent l'utilisation de packages mathématiques. J'adore et j'utilise MATLAB depuis de nombreuses années. Mon exemple de construction d'une caractéristique d'écoulement linéarisée y est fait. Un exemple peut être téléchargé à partir du lien , exécuter et déterminer indépendamment la méthode de construction d'une caractéristique de flux linéarisée.
La caractéristique d'écoulement de la turbine en question a été construite pour les valeurs fixes suivantes des paramètres de mode:
- fonctionnement en une seule étape
- pression de vapeur moyenne pression = 13 kgf / cm2,
- pression de vapeur basse pression = 1 kgf / cm2.
Contenu de l' archive Chuchueva-PT-80-linear-caractéristique-curve.rar .
1) Nomogrammes de consommation spécifique qt brut pour la production d'électricité (les points rouges marqués sont numérisés - transférés dans le tableau):
- PT80_qt_Qm_eq_0_digit.png,
- PT80_qt_Qm_eq_100_digit.png,
- PT80_qt_Qm_eq_120_digit.png,
- PT80_qt_Qm_eq_140_digit.png,
- PT80_qt_Qm_eq_150_digit.png,
- PT80_qt_Qm_eq_20_digit.png,
- PT80_qt_Qm_eq_40_digit.png,
- PT80_qt_Qm_eq_60_digit.png,
- PT80_qt_Qm_eq_80_digit.png.
2) Le résultat de la numérisation (chaque fichier csv correspond à un fichier png):
- PT-80_Qm_eq_0.csv,
- PT-80_Qm_eq_100.csv,
- PT-80_Qm_eq_120.csv,
- PT-80_Qm_eq_140.csv,
- PT-80_Qm_eq_150.csv,
- PT-80_Qm_eq_20.csv,
- PT-80_Qm_eq_40.csv,
- PT-80_Qm_eq_60.csv,
- PT-80_Qm_eq_80.csv.
3) Script MATLAB avec calculs et graphisme:
- PT_80_linear_characteristic_curve.m
4) Le résultat de la numérisation des nomogrammes et le résultat de la construction d'une caractéristique d'écoulement linéarisée sous forme de tableau:
- PT_80_linear_characteristic_curve.xlsx.
Étape 1. Traduction des nomogrammes ou des résultats de mesure dans une vue tabulaire
1. Traitement des données source
Les données initiales de notre exemple sont des nomogrammes q t bruts.
Pour numériser de nombreux nomogrammes, vous avez besoin d'un outil spécial. J'ai utilisé à plusieurs reprises une application Web à ces fins. L'application est simple, pratique, mais n'a pas suffisamment de flexibilité pour automatiser le processus. Une partie du travail doit être effectuée manuellement.
À cette étape, il est important de numériser les points extrêmes des nomogrammes qui définissent les limites de la plage de réglage de la turbine à vapeur .
Le travail consistait à marquer les points de la caractéristique de décharge dans chaque fichier png à l'aide de l' application , à télécharger le csv résultant et à collecter toutes les données dans un tableau. Le résultat de la numérisation se trouve dans le fichier PT-80-linear-caractéristique-courbe.xlsx, feuille «PT-80», tableau «Données d'entrée».
2. Apporter des unités de mesure en unités de puissance
Ensuite, sur la feuille "PT-80" nous calculons les valeurs de Q 0 selon la formule
$$ afficher $$ \ commencer {équation} Q_0 = \ frac {q_T \ cdot N} {1000} + Q_P + Q_T \ qquad (1) \ end {équation} $$ afficher $$
et nous apportons toutes les valeurs initiales à MW. Les calculs sont mis en œuvre à l'aide de MS Excel.
Le tableau résultant «Données d'entrée (puissance unitaire)» est le résultat de la première étape de l'algorithme.
Étape 2. Linéarisation de la caractéristique d'écoulement de la turbine à vapeur
1. Tester MATLAB
À cette étape, vous devez installer et ouvrir la version MATLAB non inférieure à 7.3 (il s'agit d'une ancienne version, la version 8.0 actuelle). Dans MATLAB, ouvrez le fichier PT_80_linear_characteristic_curve.m, exécutez-le et assurez-vous qu'il fonctionne. Tout fonctionne correctement, si sur les résultats de l'exécution du script sur la ligne de commande, vous voyez le message suivant:
PT_80_linear_characteristic_curve.xlsx 1 : a(N) = 2.317, a(Q) = 0.621, a(Q) = 0.255, a0 = 33.874 = 0.006, (0.57
Si vous avez des erreurs, essayez par vous-même de les corriger.
2. Calculs
Tous les calculs sont implémentés dans le fichier PT_80_linear_characteristic_curve.m. Examinons-le en plusieurs parties.
1) Nous indiquons le nom du fichier source, la feuille, la plage de cellules contenant le tableau «Données source (unité de capacité)» obtenu à l'étape précédente.
XLSFileName = 'PT_80_linear_characteristic_curve.xlsx'; XLSSheetName = 'PT-80'; XLSRange = 'F3:I334';
2) Nous lisons les données source dans MATLAB.
sourceData = xlsread(XLSFileName, XLSSheetName, XLSRange); N = sourceData(:,1); Qm = sourceData(:,2); Ql = sourceData(:,3); Q0 = sourceData(:,4); fprintf(' %s %1.0f \n', XLSFileName, toc);
Nous utilisons la variable Qm pour le débit moyen de vapeur Q p , l'indice m du milieu est moyen; de même, nous utilisons la variable Ql pour le débit de vapeur basse pression Q n , l'indice l de bas est faible.
3) Définissez les coefficients α i .
Rappelez la formule générale pour les caractéristiques d'écoulement
$$ afficher $$ \ commencer {équation} Q_0 = f (N, Q_, Q_) \ qquad (2) \ fin {équation} $$ afficher $$
et spécifiez des variables indépendantes (x_digit) et dépendantes (y_digit).
x_digit = [N Qm Ql ones(size(N,1),1)];
Si vous ne comprenez pas pourquoi la matrice x_digit a un seul vecteur (dernière colonne), alors lisez les matériaux de régression linéaire. Sur le sujet de l'analyse de régression, je recommande le livre Draper N., Smith H. Applied regression analysis . New York: Wiley, sous presse, 1981. 693 p. (disponible en russe).
Équation d'écoulement linéarisé caractéristique d'une turbine à vapeur
$$ afficher $$ \ commencer {équation} Q_0 = \ alpha_N \ cdot N + \ alpha_ \ cdot Q_ + \ alpha_ \ cdot Q_ + \ alpha_0 \ qquad (3) \ end {equation} $$ afficher $$
est un modèle de régression linéaire multiple. Les coefficients α i seront déterminés en utilisant le «grand avantage de la civilisation» - la méthode des moindres carrés. Par ailleurs, je note que la méthode des moindres carrés a été développée par Gauss en 1795.
Dans MATLAB, cela se fait sur une seule ligne.
A = regress(y_digit, x_digit); fprintf(': a(N) = %4.3f, a(Q) = %4.3f, a(Q) = %4.3f, a0 = %4.3f\n',... A);
La variable A contient les coefficients souhaités (voir le message sur la ligne de commande MATLAB).
Ainsi, la caractéristique d'écoulement linéarisé obtenue de la turbine à vapeur PT-80 a la forme
$$ afficher $$ \ commencer {équation} Q_0 = 2,317 \ cdot N + 0,621 \ cdot Q_ + 0,255 \ cdot Q_ + 33,874 \ qquad (4) \ end {equation} $$ afficher $$
4) Nous estimons l'erreur de linéarisation de la caractéristique d'écoulement obtenue.
y_model = x_digit * A; err = abs(y_model - y_digit) ./ y_digit; fprintf(' = %1.3f, (%4.2f%%)\n\n', mean(err), mean(err)*100);
L'erreur de linéarisation est de 0,57% (voir le message sur la ligne de commande MATLAB).
Pour évaluer la commodité de l'utilisation de la caractéristique d'écoulement linéarisé d'une turbine à vapeur, nous résolvons le problème du calcul du débit de vapeur à haute pression Q 0 à des valeurs de charge connues N, Q p , Q t .
Soit N = 82,3 MW, Q p = 55,5 MW, Q t = 62,4 MW, puis
$$ afficher $$ \ commencer {équation} Q_0 = 2,317 \ cdot 82,3 + 0,621 \ cdot 55,5 + 0,255 \ cdot 62,4 + 33,874 = 274,9 \ qquad (5) \ end {équation} $$ afficher $$
Permettez-moi de vous rappeler que l'erreur de calcul moyenne est de 0,57%.
Revenons à la question: pourquoi le débit linéarisé caractéristique d'une turbine à vapeur est-il fondamentalement plus pratique que les nomogrammes de consommation spécifique q t brute pour la production d'électricité? Pour comprendre la différence fondamentale dans la pratique, résolvez deux problèmes.
- Calculez Q 0 avec la précision indiquée en utilisant les nomogrammes et vos yeux.
- Automatisez le processus de calcul de Q 0 à l' aide de nomogrammes.
Evidemment, dans la première tâche, la détermination de q valeurs brutes à l'œil est lourde d'erreurs grossières.
La deuxième tâche est lourde à automatiser. Comme les valeurs q q sont grossièrement non linéaires , pour une telle automatisation, le nombre de points numérisés est dix fois plus grand que dans l'exemple actuel. La numérisation seule ne suffit pas, il est également nécessaire de mettre en œuvre un algorithme d' interpolation (recherche de valeurs entre points) de valeurs brutes non linéaires.
Étape 3. Déterminer les limites de la plage de réglage de la turbine à vapeur
1. Calculs
Pour calculer la plage de réglage, nous utiliserons un autre «bien de la civilisation» - la méthode de la coque convexe, la coque convexe.
Dans MATLAB, cela se fait comme suit.
indexCH = convhull(N, Qm, Ql, 'simplify', true); index = unique(indexCH); regRange = [N(index) Qm(index) Ql(index)]; regRangeQ0 = [regRange ones(size(regRange,1),1)] * A; fprintf(' = %d\n\n', size(index,1));
La méthode convhull () détermine les points limites de la plage de réglage donnée par les valeurs des variables N, Qm, Ql. La variable indexCH contient les sommets des triangles construits en utilisant la triangulation de Delaunay. La variable regRange contient les points limites de la plage de réglage; variable regRangeQ0 - débits de vapeur à haute pression pour les points limites de la plage de contrôle.
Le résultat du calcul se trouve dans le fichier PT_80_linear_characteristic_curve.xlsx, feuille «Résultat PT-80», tableau «Limites de la plage de réglage».
Caractéristique d'écoulement linéarisé construite. Il s'agit d'une formule (4) et de 37 points qui définissent les limites (coque) de la plage de réglage dans le tableau correspondant.
2. Vérification
Lors de l'automatisation des processus de calcul, Q 0, il est nécessaire de vérifier si un point avec les valeurs de N, Q p , Q t est à l'intérieur ou à l'extérieur de la plage de réglage (le mode n'est pas techniquement réalisable). Dans MATLAB, cela peut être fait comme suit.
Nous fixons les valeurs de N, Q p , Q t que nous voulons vérifier.
n = 75; qm = 120; ql = 50;
Nous vérifions.
in1 = inpolygon(n, qm, regRange(:,1),regRange(:,2)); in2 = inpolygon(qm, ql, regRange(:,2),regRange(:,3)); in = in1 && in2; if in fprintf(' N = %3.2f , Q = %3.2f , Q = %3.2f \n', n, qm, ql); else fprintf(' N = %3.2f , Q = %3.2f , Q = %3.2f ( )\n', n, qm, ql); end
La vérification s'effectue en deux étapes:
- la variable in1 indique si les valeurs de N, Q p sont tombées dans la projection de la coque sur l'axe N, Q p ;
- de même, la variable in2 montre si Q p , Q t sont à l'intérieur de la projection de la coque sur l'axe de Q p , Q t .
Si les deux variables sont égales à 1 (vrai), le point souhaité se trouve à l'intérieur de la coque, ce qui définit la plage de réglage de la turbine à vapeur.
Illustration de la caractéristique d'écoulement linéarisé obtenue d'une turbine à vapeur
Les «avantages les plus généreux de la civilisation» que nous avons obtenus en termes d'illustration des résultats des calculs.
Nous devons d'abord dire que l'espace dans lequel nous construisons les graphiques, c'est-à-dire l'espace avec les axes x - N, y - Q t , z - Q 0 , w - Q p , est appelé l' espace de régime (voir Optimisation du fonctionnement des centrales thermiques dans les conditions marché de gros de l'électricité et de la capacité de la Russie
) Chaque point de cet espace définit un certain mode de fonctionnement d'une turbine à vapeur. Le mode peut être
- techniquement faisable, si le point est à l'intérieur de la coque qui définit la plage de réglage,
- techniquement impossible si le point est en dehors de cette coquille.
Si nous parlons du mode de fonctionnement par condensation d'une turbine à vapeur (Q p = 0, Q t = 0), alors la caractéristique d'écoulement linéarisé est un segment en ligne droite . Si nous parlons d'une turbine de type T, la caractéristique d'écoulement linéarisée est un polygone plat dans un espace de régime tridimensionnel avec les axes x - N, y - Q t , z - Q 0 , ce qui est facile à visualiser. Pour une turbine de type PT, la visualisation est la plus difficile, car la caractéristique de flux linéarisé d'une telle turbine est un polygone plat dans un espace à quatre dimensions (pour des explications et des exemples, voir Optimisation du fonctionnement des centrales thermiques sur le marché de gros de l'électricité et de l'électricité de la Russie, section Linéarisation de la caractéristique de flux de la turbine ).
1. Illustration des caractéristiques d'écoulement linéarisées obtenues d'une turbine à vapeur
Construisons les valeurs du tableau «Données d'entrée (unité de puissance)» dans l'espace du régime.
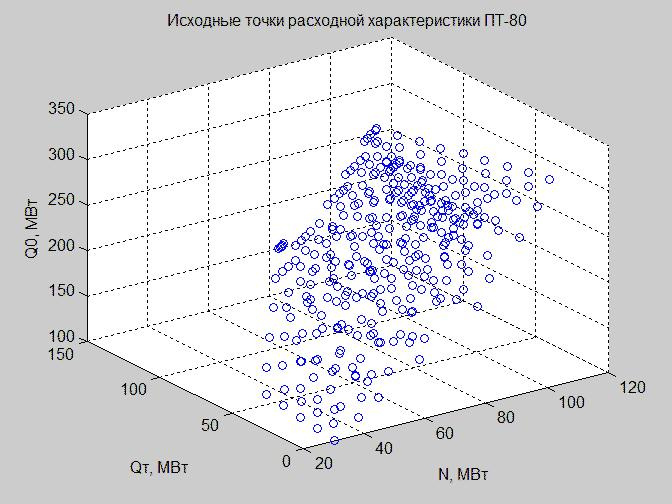
Fig. 3. Les points de départ des caractéristiques d'écoulement dans l'espace du régime avec les axes x - N, y - Q t , z - Q 0
Comme nous ne pouvons pas construire de dépendance dans un espace à quatre dimensions, nous n'avons pas encore atteint un tel niveau de civilisation, nous opérons sur les valeurs de Q n comme suit: les exclure (Fig.3), fixons (Fig.4) (voir le code pour construire des graphiques dans MATLAB).
Nous fixons la valeur de Q p = 40 MW et construisons les points de départ et la caractéristique d'écoulement linéarisé.
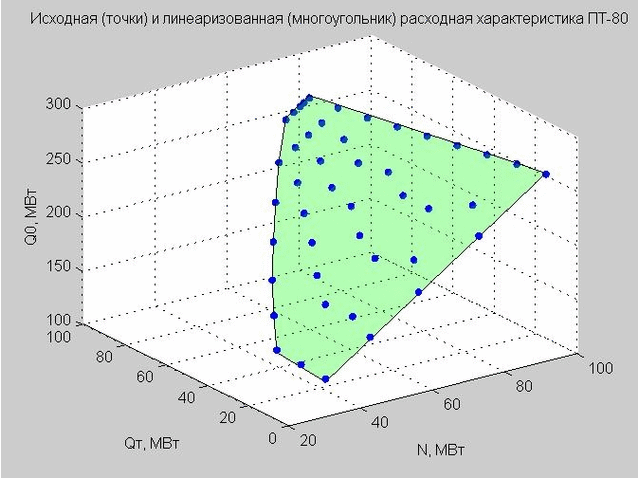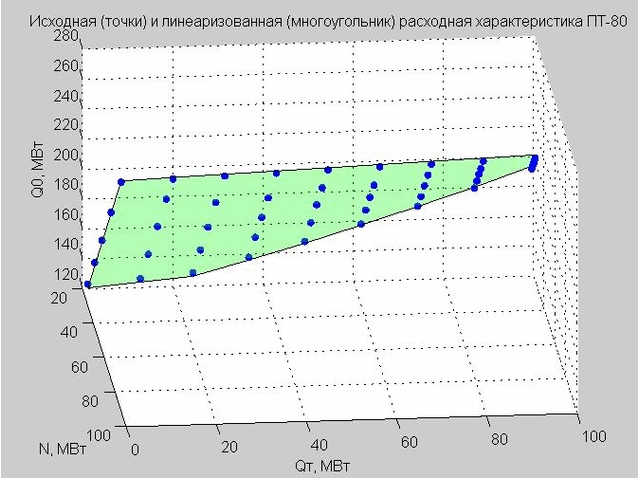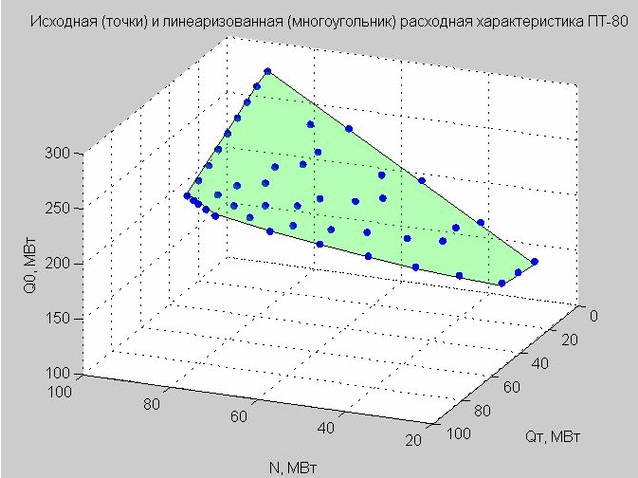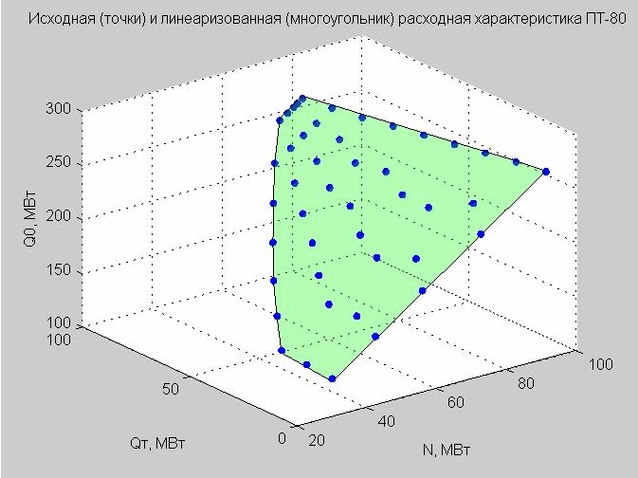
Fig. 4. Points de départ de la caractéristique de décharge (points bleus), caractéristique de décharge linéarisée (polygone plat vert)
Revenons à la formule de la caractéristique de débit linéarisé (4) que nous avons obtenue. Si nous fixons Q p = 40 MW MW, alors la formule aura la forme
$$ afficher $$ \ commencer {équation} Q_0 = 2,317 \ cdot N + 0,255 \ cdot Q_T + 58,714 \ qquad (6) \ end {equation} $$ afficher $$
Ce modèle définit un polygone plat dans un espace tridimensionnel avec les axes x - N, y - Q t , z - Q 0, par analogie avec une turbine de type T (on le voit sur la figure 4).
Il y a de nombreuses années, lors de l'élaboration de q nomogrammes bruts, une erreur fondamentale a été commise au stade de l'analyse des données initiales. Au lieu d'appliquer la méthode des moindres carrés et de construire une caractéristique d'écoulement linéarisé d'une turbine à vapeur pour une raison inconnue, ils ont fait un calcul primitif:
$$ afficher $$ \ commencer {équation} Q_0 (N) = Q_ = Q_0 - Q_ - Q_ \ qquad (7) \ fin {équation} $$ afficher $$
Soustrait du débit de vapeur à haute pression Q 0 le débit des vapeurs Q t , Q p et attribuait la différence résultante Q 0 (N) = Q e à la production d'électricité. La valeur obtenue Q 0 (N) = Q e a été divisée par N et convertie en kcal / kW · h, après avoir reçu une consommation spécifique q t brute. Ce calcul n'est pas conforme aux lois de la thermodynamique.
Chers lecteurs, vous connaissez peut-être la raison inconnue? Partagez-le!
2. Illustration de la plage de réglage de la turbine à vapeur
Voyons la coque de la plage de réglage dans l'espace du régime. Les points de départ de sa construction sont présentés sur la Fig. 5. Ce sont les mêmes points que nous voyons dans la fig. 3, cependant, le paramètre Q 0 est désormais exclu.

Fig. 5. Les points de départ des caractéristiques d'écoulement dans l'espace du régime avec les axes x - N, y - Q p , z - Q t
De nombreux points de la fig. 5 est convexe. En utilisant la fonction convexhull (), nous avons défini les points qui définissent la coque externe de cet ensemble.
La triangulation de Delaunay (un ensemble de triangles connectés) nous permet de construire la coque de la plage de réglage. Les sommets des triangles sont les valeurs limites de la plage de réglage de la turbine à vapeur PT-80 considérée.
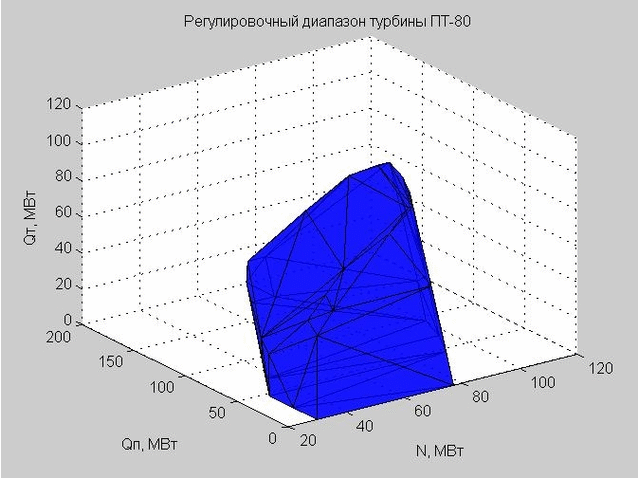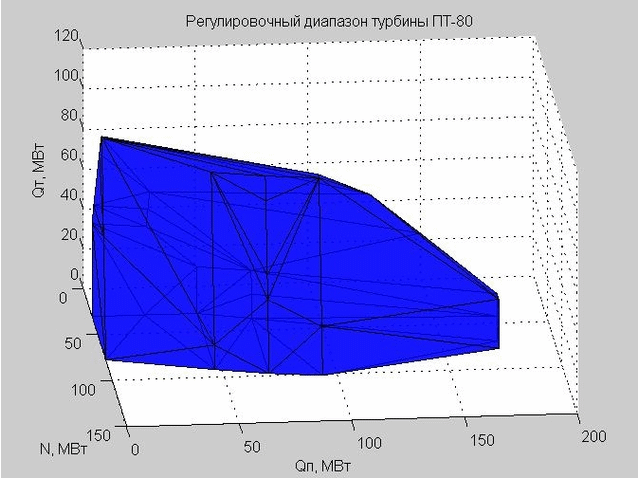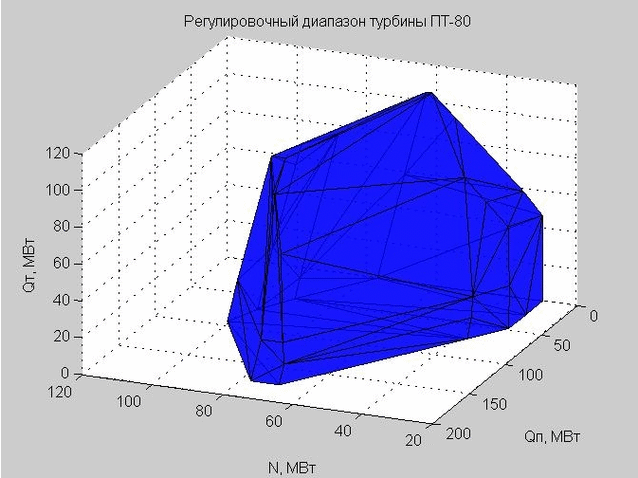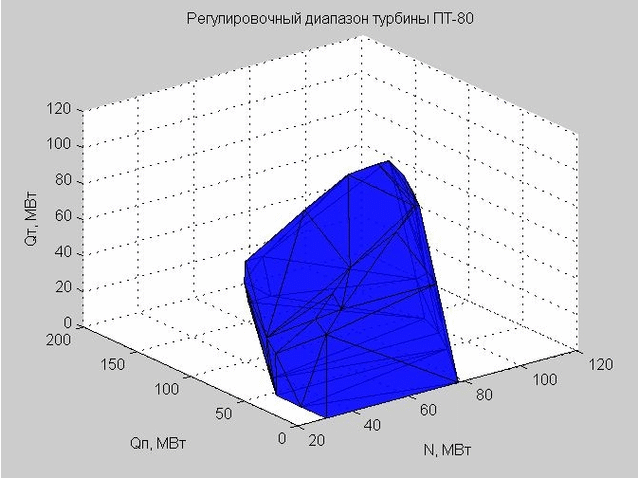
Fig. 6. La coque de la plage de réglage, représentée par de nombreux triangles
Lorsque nous avons vérifié un certain point pour entrer dans la plage de réglage, nous avons vérifié si ce point se trouve à l'intérieur ou à l'extérieur de la coque résultante.
Tous les graphiques présentés ci-dessus sont construits à l'aide des outils MATLAB (voir PT_80_linear_characteristic_curve.m).
Tâches prometteuses liées à l'analyse du fonctionnement d'une turbine à vapeur à l'aide d'une caractéristique d'écoulement linéarisée
Si vous faites un diplôme ou une thèse, je peux vous proposer plusieurs tâches dont vous pouvez facilement prouver la nouveauté scientifique au monde entier. De plus, vous ferez un travail excellent et utile.
Tâche 1
Montrez comment le polygone plat change lorsque la pression de vapeur basse pression Q t change.
Tâche 2
Montrez comment le polygone plat change lorsque la pression dans le condenseur change.
Tâche 3
Vérifier si les coefficients de la caractéristique d'écoulement linéarisé peuvent être représentés en fonction de paramètres supplémentaires du régime, à savoir:
$$ afficher $$ \ commencer {équation} \ alpha_N = f (p_ {0}, ...); \\ \ alpha_P = f (p_ {P}, ...); \\ \ alpha_T = f (p_ {T}, ...); \\ \ alpha_0 = f (p_ {2}, ...). \ end {équation} $$ afficher $$
Ici p 0 - pression de vapeur haute pression, p p - pression de vapeur moyenne pression, p t - pression de vapeur basse pression, p 2 - pression de vapeur d'échappement dans le condenseur, toutes les unités sont en kgf / cm2.
Justifiez le résultat.
Les références
Chuchueva I.A., Inkina N.E. Optimisation de la cogénération dans les conditions du marché de gros de l'énergie électrique et de la capacité de la Russie // Science et éducation: édition scientifique du MSTU. N.E. Bauman. 2015. N ° 8. S. 195-238.
Chuchueva I.A. Méthodes de calcul pour déterminer la consommation spécifique de combustible équivalent des centrales thermiques pour l'énergie électrique et thermique fournie en mode de production combinée // Science et éducation: publication scientifique du MSTU. N.E. Bauman. 2016. N ° 2. P. 135-165.
Débit linéarisé caractéristique d'une turbine à vapeur.