L'une des conséquences les plus intuitives de la théorie de la relativité d'Einstein est qu'il n'y a ni espace absolu ni temps absolu. Si vous demandez où et quand vous êtes, vous répondrez. Mais si vous et moi nous dispersons sur une longue distance, et je vous demande où et quand, comme vous le pensez, je suis, alors nos réponses ne coïncideront pas nécessairement. Il s'avère que dans la théorie générale de la relativité, il n'existe pas de méthode universelle pour déterminer l'espace et le temps (et les distances) autre que l'endroit où vous vous trouvez. En conséquence, nous avons de nombreuses façons de définir de telles choses, et c'est avec cela que la question du lecteur est liée:
J'aimerais voir votre explication du temps conforme et de la distance associée - ce que c'est, quand et comment ils sont utilisés par rapport au temps et à la distance habituels.
En utilisant des concepts tels que «temps» et «distance» dans un discours ordinaire, nous faisons de nombreuses hypothèses auxquelles nous pensons rarement.

Si vous pensez que vous pouvez me dire que là où je suis, il est 10 h 05 du matin et je suis à 700 mètres de vous, vous ne comprenez peut-être pas sur quelle base vous avez confiance en vos estimations. Vous supposez que nos montres tournent à la même vitesse, qu'elles proviennent du même endroit où nous nous sommes mis d'accord sur la valeur du temps, et que lorsque nous remontons l'horloge, elles seront également cohérentes les unes avec les autres. C'est simple, non?
Mais cela n'est possible que si deux conditions importantes sont remplies:
1. Rien ne bouge par rapport à tout le reste. Si deux objets acquièrent de la vitesse l'un par rapport à l'autre, ils connaissent un cours du temps différent (et un sentiment de distance). Les particules instables se déplaçant à des vitesses proches de la vitesse de la lumière semblent vivre plus longtemps en raison de l'étirement du temps, et les astronautes à bord de l'ISS, se déplaçant rapidement autour de la Terre, vieillissent un peu différemment des personnes immobiles sur Terre.
2. L'espace est absolument plat, ce qui n'arrive jamais. La relativité générale fonctionne dans l'Univers et, selon lui, l'existence de la matière et de l'énergie signifie que l'espace est courbé et que l'horloge se déplace à différentes vitesses en fonction de la profondeur d'immersion dans le champ gravitationnel. L'horloge au sommet de l'Empire State Building est chaque année à quelques microsecondes de l'horloge à son pied.
Les mêmes restrictions s'appliquent aux distances: le mouvement et la courbure de l'espace empêchent les observateurs de différents endroits d'adopter une norme de distance universelle. Mais pour de très grandes distances, quelque chose d'autre commence à jouer un rôle: le fait de l'expansion du tissu même de l'espace de l'Univers à l'échelle cosmique. Nous ne pouvons plus parler des distances entre les galaxies comme quelque chose qui peut être mesuré par une règle convenue, car l'espace entre les galaxies augmente avec le temps. Et cela conduit à des problèmes lorsque nous commençons à parler, par exemple, des galaxies les plus éloignées de l'univers.

Le détenteur actuel du record d'espace pour les distances est situé à un décalage vers le rouge de 11,1, ce qui signifie que pendant l'existence de l'Univers, à 13,8 milliards d'années du Big Bang, sa lumière nous est parvenue, ayant parcouru 13,4 milliards d'années. Mais à quelle distance est cette galaxie de nous? Vous pourriez, en fonction du temps passé sur le chemin, décider qu'il est à 13,4 milliards d'années-lumière - mais ce n'est guère le cas. Lorsque la lumière qui nous est parvenue a été émise par cette galaxie, elle n'était plus qu'à deux milliards d'années-lumière de nous. Grâce à l'expansion de l'Univers, nous, en utilisant le standard de mesure généralement accepté, pouvons dire que nous sommes maintenant à 32 milliards d'années-lumière de nous. La norme de distance universelle est difficile à définir dans un univers en expansion, dans lequel les distances changent avec le temps.

Ainsi, l'un des concepts que nous introduisons pour répondre à la question d'un lecteur est le concept de différents types de distances. Il nous interroge sur l'un d'entre eux - sur la
distance qui l'
accompagne . C'est l'un de mes concepts préférés: il implique que les distances dans l'univers changent en raison de l'expansion de Hubble, il exclut donc l'extension des calculs. Il est très pratique pour simuler la formation de structures de l'Univers telles que les étoiles, les galaxies, les amas et les fils. La gravité, bien sûr, y contribue, mais l'Univers s'est développé tout ce temps. En sachant comment ajuster les distances pour l'expansion, nous pouvons voir comment les structures à grande échelle de l'Univers évoluent. L'observation visuelle de cela est beaucoup plus intéressante que l'observation de l'expansion de l'Univers et d'essayer de discerner dans tout cela le processus de formation de la structure.
L'espace et le temps étant inextricablement liés au concept d'espace-temps qui les unit, nous avons besoin d'un nouveau concept de temps, correspondant à chacun des nouveaux concepts de distances que nous inventons. Le temps conforme sera le partenaire temporaire de la distance qui l'accompagne. Si nous pouvions par magie geler instantanément l'expansion entière de l'Univers à tous les endroits, alors le temps conforme correspond à combien de temps un rayon lumineux prend le temps de voyager d'un certain endroit jusqu'à vous.
Pour la galaxie la plus éloignée de l'Univers, le temps conforme sera de 32 milliards d'années. Pour la distance perçue du Big Bang, ce sera 46 milliards d'années. Et cela malgré le fait que 400 millions d'années se soient écoulées depuis le Big Bang jusqu'à l'émission de lumière par la première galaxie. Au début, l'expansion de l'Univers était si rapide - et le résultat se fait encore sentir aujourd'hui - que la différence de 14 milliards d'années de temps conforme correspond à la différence de 400 millions d'années de temps «juste» (que nous appelons simplement «temps»).
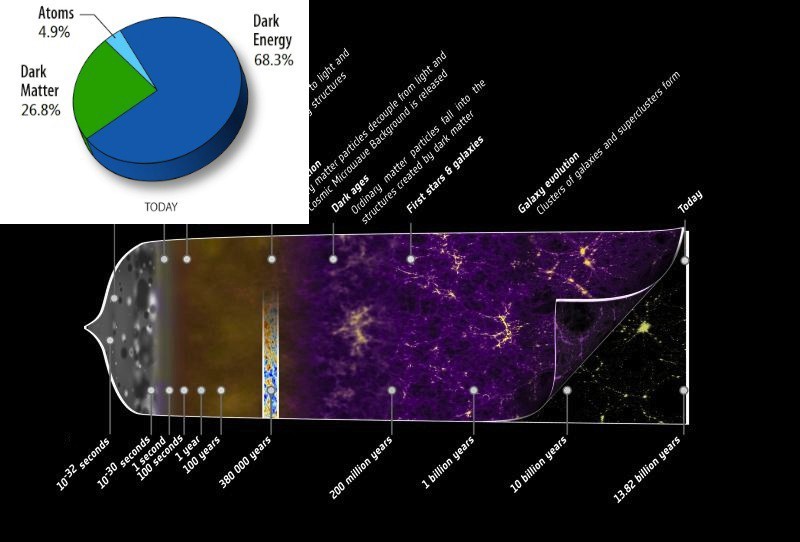
Si nous parlons d'événements qui se déroulent sur Terre, où rien ne bouge à des vitesses proches de la lumière et ne change trop dans le champ gravitationnel, alors les différents types de «distances» et de «temps» coïncideront. Mais si nous parlons de l'Univers en expansion à une échelle cosmique, alors la distance correcte et le bon moment peuvent ne pas être aussi utiles et intéressants que la distance qui l'accompagne et le temps conforme. Et la prochaine fois que vous verrez une simulation de l'Univers et que l'univers ne semble pas en expansion, gardez à l'esprit que la simulation a lieu en utilisant les distances associées, bien qu'elle puisse utiliser l'heure correcte.
Et quand vous entendez parler d'un objet très éloigné, situé à une distance de moins de 14 milliards d'années-lumière de nous, gardez à l'esprit que nous parlons très probablement d'une distance qui l'accompagne. Selon nos règles habituelles et correctes, cette distance est susceptible d'être beaucoup plus grande!