Masse, énergie, impulsion et loi de conservation

De nombreuses propriétés obscures du monde sont associées à la nature de la masse et de l'énergie (ainsi qu'à l'élan). Nous avons tous entendu ces mots, et beaucoup d'entre nous ont une vague idée de leur signification. Bien sûr, les significations des mots "masse" et "énergie" en anglais et dans d'autres langues sont nombreuses. Malheureusement, aucun d'entre eux ne coïncide avec ceux que les physiciens ont en tête. Essayez de mettre de côté ces sens des mots et travaillez avec des concepts physiques exacts - sinon vous serez complètement confus.

Il convient de noter qu'il ne faut pas rappeler une autre paire populaire, «substance et énergie» avec l'expression «masse et énergie». Beaucoup de gens mentionnent la dernière phrase comme si la matière et l'énergie étaient les deux faces d'une même médaille. Mais ce n'est pas le cas. La matière et l'énergie entrent dans différentes catégories, comme les pommes et les orangs-outans. Une substance, peu importe comment la définir, est une classe d'objets existant dans l'Univers, et la masse et l'énergie ne sont pas des objets, mais les propriétés que ces objets possèdent. La masse et l'énergie sont intimement liées les unes aux autres et méritent une explication générale.

Pour comprendre la masse et l'énergie, vous devez leur donner un élan et discuter des différences et des relations de ces quantités.

Énergie

Le mot «énergie» a plusieurs significations. Lorsque nous tombons malades, nous disons que nous n'avons plus d'énergie, faisant référence à la force et à la motivation. Quand nous disons que quelqu'un est plein d'énergie, nous voulons dire sa forte activité. Nous nous plaignons de la hausse des prix de l'énergie, en référence au carburant. Nous parlons de l'énergie spirituelle comme quelque chose d'incommensurable, mais important, peut-être une forme de charisme. Et tous ces concepts se chevauchent, nous choisissons donc un mot pour les décrire. Mais en physique, l'énergie est une chose complètement différente. Du point de vue de la physique, l'une de ces définitions sera confondue à tort avec le physique. En physique, il faut respecter un terme physique afin de ne pas obtenir les mauvaises réponses et de ne pas être complètement confus.

Malheureusement, le concept d '«énergie» en physique est très difficile à décrire comme le font les dictionnaires - avec une courte phrase significative. Mais ne pensez pas mal - le tout est l'imperfection du langage naturel, et non pas que le concept d'énergie en physique soit vague. Dans tout système physique donné, il est parfaitement clair quelle est son énergie, à la fois dans le sens de sa mesure expérimentale et dans le sens des calculs (s'il existe des équations décrivant le système).

L'une des raisons pour lesquelles l'énergie est si difficile à décrire est qu'elle peut prendre de nombreuses formes, et toutes ne sont pas faciles à comprendre. Voici trois variétés courantes:

1. L'énergie peut être enfermée dans la masse d'un objet. Ici, j'appelle cette option «énergie de masse» (grâce à l'équation bien connue E = mc ^{2, l'} énergie se lie à la masse. Elle est aussi appelée «énergie de repos», car c'est l'énergie d'un objet au repos, c'est-à-dire sans mouvement).

2. Deuxièmement, l'énergie est associée au mouvement d'un objet. Ici, je l'appelle «énergie de mouvement», et le terme technique pour cela est l'énergie cinétique. Cette option est intuitivement facile à saisir, car les objets en mouvement rapide ont plus d'énergie que ceux en mouvement lent. De plus, un objet lourd a plus d'énergie de mouvement qu'un objet léger se déplaçant à la même vitesse.

3. L'énergie peut être stockée dans la relation des objets (et est généralement appelée "potentiel"). Il est stocké dans une source étirée, dans l'eau derrière le barrage, dans l'interaction gravitationnelle de la Terre et du Soleil, dans les interactions des atomes dans la molécule. Il existe de nombreuses façons de stocker l'énergie. Cela semble vague, mais la langue est à blâmer. Dans tous ces cas, il existe des formules exactes qui décrivent l'énergie stockée dans le système et des moyens bien définis pour la mesurer.

Le troisième type d'énergie est lié à ce que j'appellerai l'énergie d'interaction, et c'est le concept le plus déroutant de tous. Contrairement à l'énergie de masse et à l'énergie de mouvement, qui sont toujours supérieures ou égales à zéro, l'énergie des interactions peut être positive et négative. Jusqu'à présent, je vais quitter ce sujet, mais nous y reviendrons.

L'énergie est une quantité spéciale d'une grande importance pour la physique. La raison de cette importance est qu'elle est "préservée". Qu'est-ce que cela signifie?

Si vous commencez l'observation avec un objet ou avec un ensemble d'objets - nous les appellerons un «système d'objets» - possédant une certaine quantité d'énergie au moment initial (n'oubliez pas de calculer toute l'énergie - masses, mouvements, énergie stockée de tous types, etc.), puis certaines parties du système n'interagiront qu'entre elles et avec rien d'autre, puis à la fin de l'observation, la quantité totale d'énergie possédée par ces objets sera la même qu'au début. L'énergie totale du système est conservée - sa quantité totale ne change pas. Cela peut changer de forme, mais si vous gardez une trace de toutes les variétés, à la fin, ce sera autant qu'au début.

Cette règle fonctionne même si certains objets disparaissent et cèdent la place à d'autres, par exemple, si une particule du système se désintègre en deux autres fusionnant dans le système.

Pourquoi l'énergie est-elle économisée? En raison du principe mathématique, corrélant le fait que les lois de la nature ne changent pas avec le temps, avec l'existence d'une quantité conservée, que nous appelons par définition «énergie».

Nous devons la définition la plus célèbre et la plus générale de ce principe à Emmy Noether , l'un des plus grands physiciens mathématiques du siècle précédent, un contemporain d'Einstein. Certains membres de la communauté physique et mathématique l'ont traitée avec un profond respect , mais à cette époque, dans son Allemagne natale, elle a souffert de discrimination fondée sur le sexe et la nationalité (là-bas, ils ont bloqué les tentatives de lui attribuer le titre de professeur à Göttingen , et de là, elle a dû fuir après les nazis sont arrivés au pouvoir). Après avoir émigré aux États-Unis, après seulement deux ans d'enseignement au Brin-Mar College (qui n'accepte à ce jour que des femmes pour la formation), elle est décédée d'un cancer.

Le célèbre théorème de Noether (en fait, ce sont deux théorèmes étroitement liés) nous dit que s'il y a symétrie dans les lois de la nature - dans notre cas, cela signifie que les lois de la nature sont les mêmes à tout moment - alors cela préserve une certaine quantité - dans notre cas, l'énergie .

De plus, le théorème nous dit exactement quelle est l'ampleur - quelles sont les différentes formes d'énergie pour un système donné d'objets qui doivent être ajoutées afin d'obtenir l'énergie totale. C'est pourquoi les physiciens savent toujours exactement ce qu'est l'énergie, et pourquoi il est plus facile d'obtenir à l'aide d'équations que de définir en mots.

Impulsion

La situation avec l'élan est à peu près la même qu'avec l'énergie. Les lois de la nature sont partout les mêmes. En gros, les expériences donnent les mêmes réponses, que vous les passiez au nord ou au sud d'ici, à l'ouest ou à l'est, au sommet d'un bâtiment ou dans un puits profond. Choisissez n'importe quelle direction dans l'espace. Ensuite, selon Noether, l'élan dans cette direction est conservé. Puisqu'il y a trois dimensions dans l'espace, il est possible de se déplacer dans trois directions indépendantes différentes et il existe trois lois de conservation indépendantes. Vous pouvez choisir trois directions, à condition qu'elles soient différentes. Par exemple, vous pouvez choisir des impulsions dans les directions nord-sud, ouest-est et haut-bas comme trois lois de conservation. Ou vous pouvez en choisir trois autres - dans la direction de et vers le Soleil, le long de l'orbite de la Terre dans les deux directions, et de haut en bas par rapport au plan du système solaire. Votre choix n'a pas d'importance, car l'élan est stocké dans toutes les directions.

La forme d'impulsion la plus simple est due au simple mouvement d'objets, et c'est quelque chose qui peut être imaginé intuitivement: si un objet se déplace dans une certaine direction, alors il a une impulsion dans cette direction, et plus il se déplace rapidement, plus cette impulsion est grande. Et un objet plus lourd a une plus grande dynamique qu'un objet léger s'il se déplace à la même vitesse.

L'une des conséquences intéressantes de cette conservation: si vous avez un système d'objets immobile (c'est-à-dire que le système dans son ensemble ne bouge pas si vous faites la moyenne de tous les mouvements de ses objets constitutifs), alors il restera immobile, à moins qu'il ne lui soit donné un mouvement externe impact. La raison en est que dans un système fixe, la quantité de mouvement totale est nulle, et puisque la quantité de mouvement est maintenue, elle restera nulle pour toujours à moins que quelque chose n'intervienne de l'extérieur du système.

Masse et sa relation avec l'énergie et l'élan

Passons maintenant à la masse

Malheureusement, beaucoup de confusion est associée à la masse - après la publication des travaux d'Einstein sur la théorie de la relativité pendant un certain temps, il y avait deux concepts de masse. Et un seul d'entre eux (celui sur lequel Einstein s'est arrêté, et qui est parfois appelé la "masse invariante" ou "masse au repos pour la distinguer du terme déjà devenu archaïque" masse relativiste "), est encore utilisé en physique des particules. Dans un article séparé, je vais l'expliquer plus en détail.


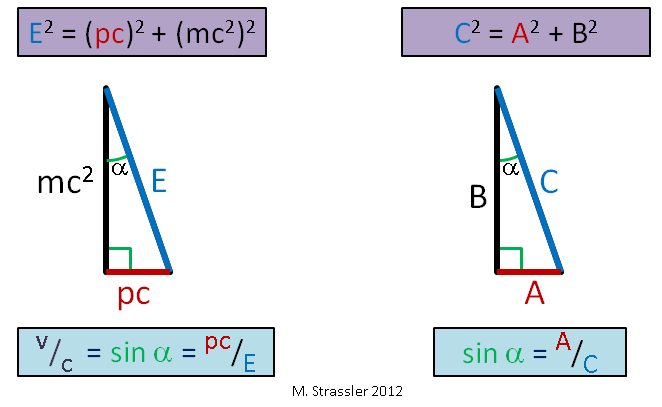Fig. 1

Par masse m, que j'utilise dans les articles, on entend cette masse qui lie directement l'énergie et l'élan. Pour un objet se déplaçant sans l'influence de forces externes (n'interagissant pas de manière significative avec d'autres objets), Einstein a suggéré (et cela a été confirmé par des expériences) que son énergie E, sa quantité de mouvement p et sa masse m satisfont la simple égalité pythagoricienne:

$$ $$E ^ 2 = (p c) ^ 2 + (mc ^ 2) ^ 2 \ qquad (équation n ° 1)$$

Rappelez-vous le vieux Pythagore qui prétendait que pour un triangle rectangle avec les côtés A et B et l'hypoténuse C, l'égalité $$$C ^ 2 = A ^ 2 + B ^ 2$ ? Il s'agit d'une connexion du même type - voir fig. 1. Chez nous, c est une vitesse constante qui, comme nous le verrons, sert de limite de vitesse universelle. Nous verrons également pourquoi on l'appelle la «vitesse de la lumière».

Selon les équations d'Einstein, la vitesse d'un objet divisée par la limite de vitesse c n'est que le rapport de pc à E:

$$ $$v / c = (p c) / E \ qquad (équation # 2)$$

Autrement dit, le rapport de la jambe horizontale à l'hypoténuse. Il est également égal au sinus de l'angle α de la Fig. 1. Alors, ici, citoyens. Et comme les jambes d'un triangle rectangle sont toujours plus courtes que l'hypoténuse (le sinus de n'importe quel angle est toujours inférieur ou égal à 1), la vitesse d'un objet ne peut pas dépasser s, la limite de vitesse universelle. Avec une augmentation de la vitesse d'un objet de masse fixe, p et E deviennent très grands (Fig.2), mais E est toujours supérieur à pc, donc v est toujours inférieur à c!


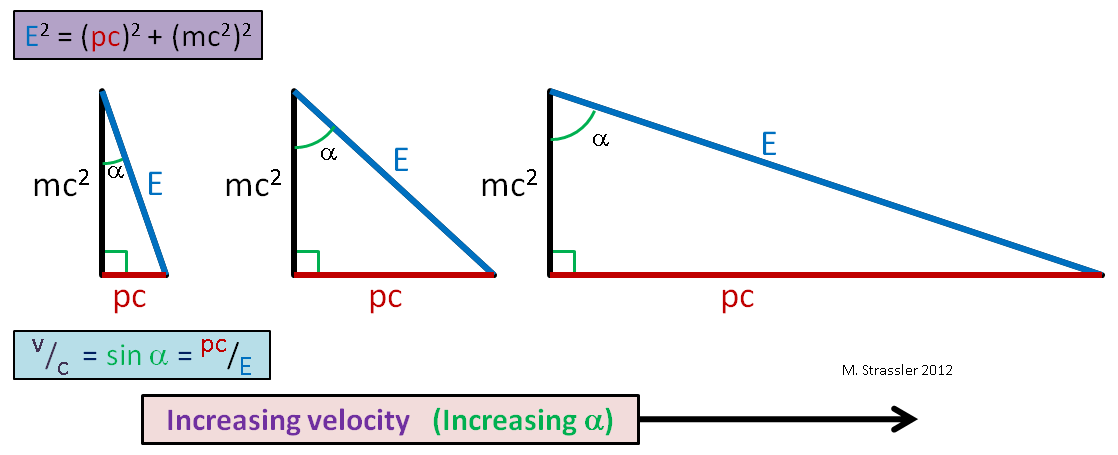Fig. 2

Notez maintenant que si l'objet ne bouge pas, son momentum p est égal à zéro et le rapport dans l'équation 1 se réduit à:

$$ $$E ^ 2 = (mc ^ 2) ^ 2, \ quad ou \ quad E = mc ^ 2$$

La célèbre formule d'Einstein, la relation de la masse à une quantité fixe d'énergie (ce que j'appelle l'énergie de masse), est simplement une déclaration correspondant au fait que lorsqu'un triangle dégénère en une ligne verticale, comme dans la Fig. 3 à gauche, son hypoténuse devient de la même longueur que la jambe verticale. En même temps, cela ne signifie pas que l'énergie est toujours égale à la masse multipliée par carré s. Cela ne fonctionne que pour un objet au repos avec un élan nul.


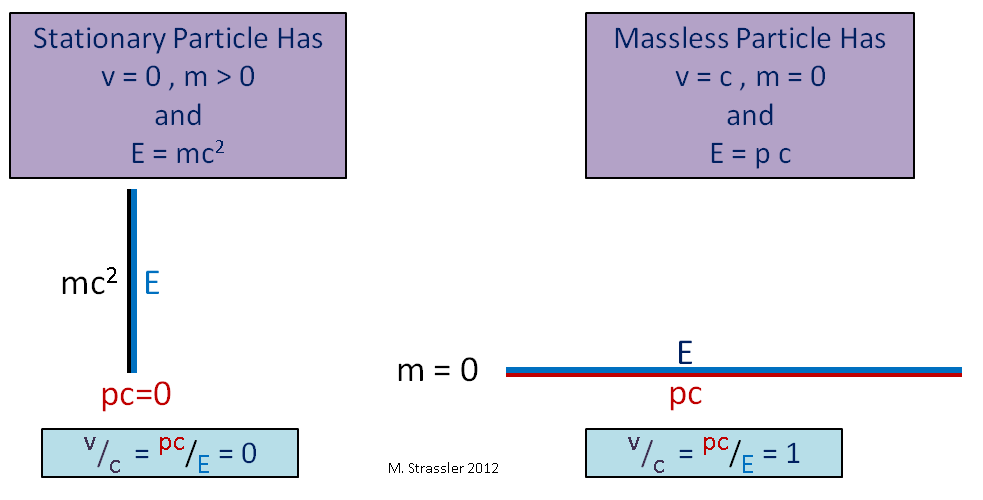Fig. 3

Autre observation intéressante: pour une particule sans masse, la jambe verticale du triangle est nulle, et l'hypoténuse et la jambe horizontale sont les mêmes, comme sur la Fig. 3. Dans ce cas, E est pc, ce qui signifie que v / c = 1 ou v = c. On voit qu'une particule sans masse (par exemple, un photon, une particule de lumière) se déplace inévitablement à une vitesse de c. Par conséquent, la vitesse de la lumière est la même que la limite de vitesse universelle, art.

D'un autre côté, si nous prenons une particule de masse, comme dans la Fig. 4, peu importe l'ampleur de l'élan et de l'énergie, E sera toujours un peu plus que p * c, donc la vitesse sera toujours inférieure à s. Les particules sans masse doivent se déplacer à vitesse maximale. La vitesse des particules massives devrait être inférieure.


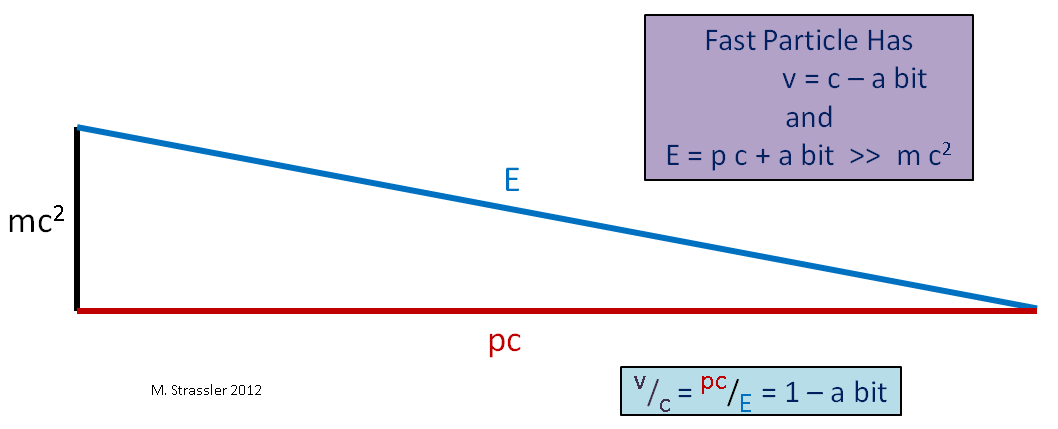Fig. 4. Ici ">>" signifie "bien plus"

Imaginez un autre cas limite, un objet massif se déplaçant lentement (par rapport à la vitesse de la lumière), comme une voiture. Étant donné que sa vitesse v est bien inférieure à c, sa quantité de mouvement p fois c sera bien inférieure à E et, comme le montre la Fig. 5, E sera un peu plus que mc ² . Par conséquent, l'énergie de mouvement d'un objet lent E - mc ^{2 est} bien inférieure à l'énergie de sa masse mc ² , et pour un objet rapide, l'énergie de mouvement peut être rendue arbitrairement grande, comme nous l'avons vu sur la Fig. 4.

Un point subtil: l'élan n'est pas seulement un nombre, mais aussi un vecteur. Il a de l'ampleur et de la direction. Il est orienté vers le mouvement de la particule. Lorsque j'écris p, je n'indique que la valeur. Dans de nombreux cas, il est nécessaire de suivre la direction de l'impulsion, bien que dans l'équation n ° 1, qui relie l'impulsion à l'énergie et à la masse, ce n'est pas nécessaire.


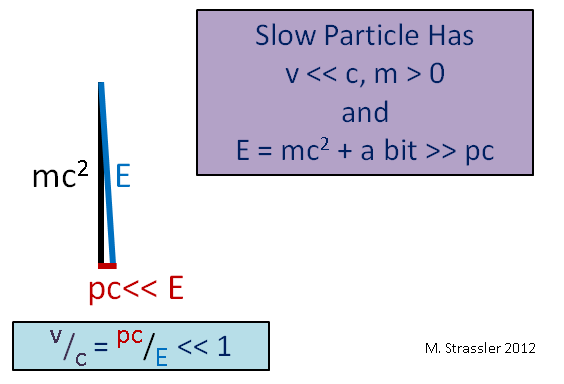Fig. 5

Autre point subtil: j'ai utilisé des triangles et de la trigonométrie simple, car elle est connue de tous depuis l'école. Les experts doivent être plus prudents - vous pouvez correctement comprendre les équations d'Einstein en utilisant des fonctions hyperboliques qui ne sont généralement pas trouvées par les amateurs, mais sont extrêmement importantes pour comprendre la structure de la théorie et rendre les choses plus compréhensibles telles que l'ajout de vitesse, la compression de distance, etc. Les gens qui ne prétendent pas être des experts peuvent ignorer cela.

Mais la vitesse est-elle relative? ..

Si vous lisez attentivement le texte, quelque chose peut déjà vous surprendre. Vous savez que la vitesse d'une particule - ou de tout ce qui se déplace plus lentement que la lumière - dépend du point de vue.

Si vous vous asseyez à la maison et lisez un livre, vous direz que la vitesse du livre est nulle (et elle repose vraiment par rapport à vous), par conséquent, il n'a pas d'élan et d'énergie de mouvement, seulement de l'énergie de masse. Mais si je me tenais sur la lune, je vous rappellerais que la Terre tourne, alors cette rotation vous captive et vous déplace par rapport à moi à une vitesse de centaines de kilomètres par heure. Donc, vous et votre livre auriez l'impulsion de mon point de vue.

Qui a raison?

La variante de la relativité selon Galileo - le premier principe de la relativité - affirme que nous avons tous les deux raison. La variante de la relativité d'Einstein est d'accord avec le point de vue de Galileo selon lequel les deux ont raison, mais apporte des ajustements importants à la façon dont les disciples de Galileo indiqueraient l'énergie, l'élan et la masse du livre, plaçant ces quantités dans la relation pythagoricienne de l'équation n ° 1.

Mais si tout va bien, quel E et quel p dois-je remplacer dans le rapport énergie / impulsion / masse, $$$E ^ 2 = (p c) ^ 2 + (mc ^ 2) ^ 2$ ? Remplacez E et p mesurés par vous en lisant le livre, c'est-à-dire E = mc ² et p = 0? Ou remplacer E et p, que le livre a de mon point de vue, lorsque vous vous déplacez avec la Terre?

La réponse à cette question contient toute l'essence de l'équation d'Einstein n ° 1. Chaque observateur mesurera différentes valeurs de E et p pour le livre, selon la vitesse à laquelle le livre se déplacera par rapport à lui. Mais pour tous les observateurs, l'équation $$$E ^ 2 = (p c) ^ 2 + (mc ^ 2) ^ 2$ sera vrai!

La magie! Mais en fait, le génie est une idée qui est venue en 1905 sur la façon de remplacer l'ensemble d'équations proposé par Newton et ses disciples par un nouvel ensemble étonnant d'équations, qui coïncide toujours avec toutes les expériences précédentes, mais s'est avéré être une représentation plus précise de la réalité. Il est difficile d'imaginer combien il était nécessaire de changer la façon de penser pour y penser jusqu'à ce que vous compreniez à quel point tout pourrait mal tourner pendant la formation de la nouvelle théorie, et combien d'autres équations différentes contenant des contradictions avec les mathématiques ou avec des expériences précédentes, vous pouvez Ce serait d'offrir (et les gens les ont offerts). Par exemple, le travail des physiciens novices me vient constamment, essayant de «corriger» les équations d'Einstein, mais je n'ai jamais vu aucun d'entre eux vérifier la cohérence interne de leurs équations. C'est une tâche très difficile et la raison de l'échec de la plupart des théories.

Mais comment conserver l'énergie et l'élan?

Attendez une minute, dites-vous, lorsque votre tête est prête à exploser et à tout éclabousser autour de vous avec votre cerveau (je me souviens de cette sensation moi-même), mais l'énergie et l'élan doivent être préservés! Alors, comment différents observateurs peuvent-ils être en désaccord avec ce qu'ils sont?

Il y a encore plus de magie qui, soit dit en passant, était antérieure à Einstein. Croyez-moi, l'Univers est un comptable très, très intelligent, et malgré le fait que différents observateurs ne seront pas d'accord sur l'énergie disponible dans un objet ou un système d'objets, ils conviendront tous que cette énergie ne change pas avec le temps. Il en va de même pour l'élan.

Mais la masse est très différente de l'énergie et de l'élan. Premièrement, la masse n'est pas conservée. Dans la nature, il existe de nombreux processus qui modifient la masse totale d'un système: par exemple, une particule de Higgs massive peut se désintégrer en deux photons sans masse. Aucune symétrie n'est associée à la masse, et donc Noether n'a pas de loi de conservation pour nous. Deuxièmement, contrairement à l'énergie et à la quantité de mouvement, dont les valeurs dépendent de l'observateur (en particulier, de sa vitesse par rapport aux objets mesurés), tous les observateurs seront d'accord avec la masse m de l'objet. Et ce n'est pas du tout évident, et cela se produit parce que les équations d'Einstein fonctionnent terriblement astucieusement.

Alors qu'avons-nous

À l'heure actuelle, nous avons plusieurs, à première vue, des connaissances contradictoires. Nous savons que:

• L'énergie et l'élan d'un système physique isolé sont conservés (l'énergie totale et l'élan total d'un système isolé ne changent pas avec le temps) du point de vue de tout observateur.
• Différents observateurs se déplaçant les uns par rapport aux autres évalueront différemment les valeurs de l'énergie et de l'élan du système!
• La somme des masses des objets qui composent le système n'est pas sauvegardée, elle peut changer.
• Mais tous les observateurs seront d'accord avec la masse de l'objet.

Deux autres faits et deux conclusions doivent être ajoutés à cette liste:

La masse du système physique des objets n'est pas égale à la somme des masses des objets qui composent ce système.

Au lieu de cela, la masse du système physique, sur laquelle tous les observateurs sont d'accord, est déterminée par son énergie et son élan, et satisfait sa version de l'équation n ° 1:

$$ $$(E_{system})^2 = (p_{system} c)^2 + (m_{system} c^2)^2 \qquad ( №1')$$

Il s'avère qu'une loi de conservation supplémentaire n'est pas nécessaire, et que bien que la somme des masses des objets qui composent le système ne soit pas conservée, la masse du système est conservée, car elle est liée par l'équation n ° 1 'à l'énergie et à l'élan du système qui sont conservés.

La masse du système d'objets est le seul élément de notre liste qui soit simultanément préservé et non sujet à débat par les observateurs.

Il suffit de se rappeler que la masse du système d'objets n'est pas la somme des masses des objets qui composent le système, mais ce qui est donné par l'équation n ° 1 '.

Alors essayez de l'expliquer, voyez comment cela fonctionne. Un exemple vivant vaut mille mots. Prenons comme exemple de système la chose la plus en vogue, à savoir la particule de Higgs (ayant une masse de 126 GeV / s ² ), et voyez comment les diverses déclarations faites ci-dessus fonctionnent quand il se désintègre en deux photons.

Une particule de Higgs, deux photons et trois observateurs

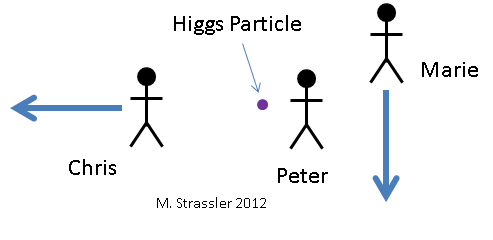Fig. 6. Trois observateurs observent la particule de Higgs. Par rapport à elle, Petya (Peter) ne bouge pas, Masha (Marie) descend et Kostya (Chris) se déplace vers la gauche.

Voyons comment la particule de Higgs se désintègre en deux photons, du point de vue de trois observateurs différents. Ils sont représentés sur la fig. 6 avec la particule de Higgs qu'ils regardent. Bien sûr, ils ne peuvent pas la voir à travers les yeux, car elle existe trop peu de temps et elle est trop petite. Ils doivent utiliser une sorte d'équipement scientifique. Pour Petit, la particule de Higgs ne bouge pas. Masha se déplace vers le bas par rapport à Petit. Kostya se déplace vers la gauche par rapport à Petit. Donc, pour Masha, la particule de Higgs monte et pour Bone - vers la droite. Trois observateurs voient comment une particule se désintègre selon la fig. 7. Petya voit que Higgs se désintègre en deux photons de la même énergie, l'un se déplaçant vers le haut et l'autre vers le bas. Masha voit que Higgs se désintègre en deux photons d'énergies différentes, et qu'une énergie se déplaçant vers le haut a plus d'énergie qu'une énergie se déplaçant vers le bas.Kostya voit Higgs se désintégrer en deux photons se dirigeant de haut en bas. Calculons les énergies et les impulsions attribuées aux Higgs et aux deux photons par les observateurs, et comment chacun d'entre eux arrivera à la conclusion que l'énergie et l'impulsion sont conservées pendant la décroissance.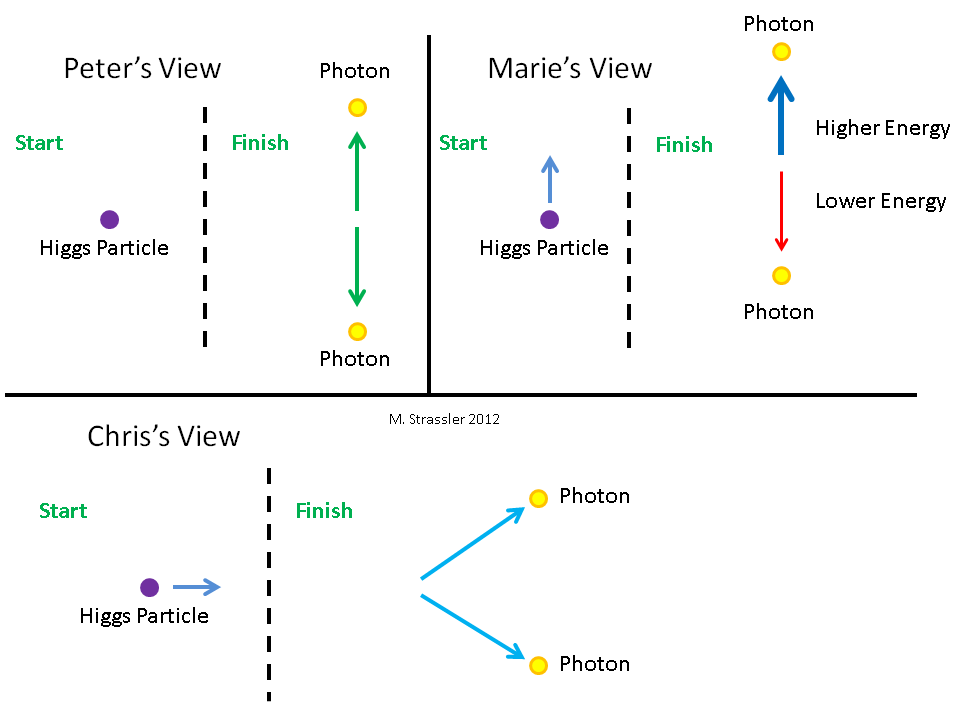

Désintégration des particules de Higgs

Dans un premier temps, nous analysons la particule de Higgs du point de vue de Petit. Petya regarde (à l'aide d'instruments de mesure) la particule de Higgs, et que voit-il? (Je mettrai un tiret sur tout ce que Petya voit, puis nous le comparerons avec les observations de Masha et Kostya). Higgs ne bouge pas, donc son élan$$$\overline{p_0}$est égal à zéro, et selon l'équation n ° 1 lui, avec sa masse m = 126 GeV / c ^{2, l'} énergie sera$$$\overline{E_0} = m c^2 = 126$

Maintenant, selon la conservation de l'énergie et de l'élan, un système composé d'une particule de Higgs conservera toute l'énergie et l'élan après la décroissance. Et il en sera ainsi jusqu'à ce qu'aucune force extérieure n'affecte Higgs. Vous pouvez vous demander si nous devons nous soucier de la gravité, car la gravité sera une influence externe qui peut changer l'élan. Ma réponse est que dans le court laps de temps où Higgs se désintègre, l'effet de la gravité sera si petit que si je vous disais à quel point il est vraiment petit, vous ririez. Oubliez ça.

Ainsi, lorsque Higgs se désintègre, les énergies des particules qui composent ses résidus devraient totaliser 126 GeV, et le momentum des particules (étant donné que le momentum n'est pas seulement une quantité, mais aussi une direction - un vecteur) totalisera zéro.

Deux photons sans masse dans lesquels les désintégrations de Higgs peuvent se diffuser dans n'importe quelle direction, mais pour simplifier l'exemple, imaginez qu'ils se diffusent verticalement - l'un vers le haut et l'autre, rebondissant dessus, vers le bas. (Un peu plus tard, nous verrons pourquoi ils devraient voler dans des directions opposées).

Quelle dynamique les photons ont-ils? C'est simple. Premièrement, l'impulsion totale du système - la somme des impulsions de deux photons - doit être nulle, car Higgs avait une impulsion nulle avant la décroissance (du point de vue de Petit). Maintenant, chacun des photons a une impulsion d'une certaine ampleur et d'une certaine direction. Au total, ils peuvent donner zéro dans un seul sens - s'ils sont de même ampleur et dans la direction opposée. Si l'un monte, l'autre doit descendre et leur taille doit être la même.


Fig. 8: ce que Petya voit

Deuxièmement, l'énergie totale du système est la somme des énergies de deux photons. En effet, il n'y a pas d'énergie d'interaction entre eux (sauf pour une attraction gravitationnelle extrêmement petite, que vous pouvez oublier). Bien sûr, puisqu'ils n'ont pas de masses, alors toute leur énergie est dans l'énergie du mouvement. De plus, dans le cas d'une particule sans masse, l'équation n ° 1 suggère que E = pc, où p est l'élan. Pour cette raison, deux photons avec les mêmes impulsions doivent avoir la même énergie. Et puisque ces deux énergies devraient s'additionner à l'énergie de la particule de Higgs, l'énergie de chaque photon devrait être égale à la moitié de l'énergie de la particule de Higgs.

$$ $$\overline E_1 = \overline E_2 = 1/2 (126 ) = 63$$

Et puisque pour une particule sans masse p = E / c, alors

$$ $$\overline p_1 = 63 /c \uparrow \\ \overline p_2 = 63 /c \downarrow$$

Et il est affiché sur la fig. 8.

L'énergie et l'élan sont conservés, mais pas la masse, car les photons n'ont pas de masse, mais Higgs en avait. Et la masse du système? Quelle est la masse d'un système de deux photons? Non nul. Évidemment ce qu'elle est. De la même manière que pour Higgs lui-même (à partir duquel tout le système était composé à l'origine), un système de deux photons a la même énergie et la même impulsion que Higgs:

$$ $$E_{system} = \overline E_1 + \overline E_2 = 63 + 63 = 126 \\ p_{system} = \overline p_1 \uparrow + \overline p_2 \downarrow = 63 /c \uparrow + 63 /c \downarrow = 0$$

Et depuis pour Petit $$$p_{system} = 0$ ,

$$ $$m_{system} = E_{system} / c^2 = 126 /c^2$$

C'est la masse de Higgs. La masse du système n'a pas changé pendant la décroissance, comme prévu.

L'observateur pour qui Higgs monte

Masha descend par rapport à Peta, donc de son point de vue, Petya et Higgs montent. Supposons que Higgs se déplace à une vitesse de v = 0,8 s, soit 4/5 de la vitesse de la lumière par rapport à lui. Contrairement à Petya, du point de vue de Masha, Higgs a une impulsion non nulle, et les impulsions des photons se révèlent être de magnitude différente, mais toujours multidirectionnelles - en conséquence de quoi la somme de leurs impulsions sera non nulle.


Fig. 9: comment Masha voit la désintégration de la particule de Higgs.

Comment calculer le momentum et l'énergie des Higgs et les deux photons dans lesquels elle se désintègre, du point de vue de Masha? Pour ce faire, nous avons besoin d'un autre ensemble d'équations d'Einstein simples. Supposons que, du point de vue d'un certain observateur, l'objet ait l'élan p et l'énergie E. Ensuite, du point de vue d'un autre observateur se déplaçant à la vitesse v dans la direction de l'objet (ou contre lui), l'élan et l'énergie de l'objet seront exprimés comme suit:

$$ $$p = γ (\overline p+ v \overline E/c^2) \qquad ( №3) \\ E = γ (\overline E + v \overline p) \qquad ( №4)$$

Où γ satisfait une autre équation de Pythagore:

$$ $$1 = v^2/c^2 + 1/γ^2 \qquad ( №5)$$

selon Einstein. Cela nous permet d'effectuer des transformations entre ce que Petya voit et ce que Masha voit (ou tout autre observateur se déplaçant à la vitesse v). Ce que nous trouvons est montré sur la Fig. 9.

Pour comparer les observations de Masha avec celles de Petya, nous avons besoin de v et γ. Je soutiens que si v = 4/5 c, alors γ = 5/3.

Vérifions en utilisant l'équation n ° 5: 1 = (4/5) 2 + (3/5) 2 = 16/25 + 9/25 = 25/25

Petya dit qu'avec Higgs$$$p_0=0, E_0=126$. Et Masha? Elle dit que:

$$ $$p_0 = γ v \overline E_0 = (5/3) (4/5) \overline E_0 = 168 /c \uparrow \\ E_0 = γ \overline E_0 = (5/3) \overline E_0 = 210$$

Petya affirme que deux photons $$$\overline E_1 = \overline E_2 = 63$, et pour chacun d'eux E = p c. Maintenant, nous pouvons calculer ce que Masha voit en utilisant les équations n ° 4 et n ° 4.

$$ $$E_1= γ (1+v) \overline E_1 = 189 , p_1 = E_1/c \uparrow$$

$$ $$E_2= γ (1-v) \overline E_2= 21 , p_2 =E_2/c \downarrow$$

Ça marche! L'énergie est également conservée du point de vue de Mary, car

$$ $$E_0 = 210 \\ E_1 + E_2 = (189 + 21) = 210$$

L'impulsion est également enregistrée:

$$ $$p_0 = 168 /c \uparrow \\ p_1 + p_2 = 189 /c \uparrow + 21 /c \downarrow = (189 – 21) /c \uparrow = 168 /c \uparrow$$

La masse du système coïncide avec la masse de Higgs avant et après désintégration, car avant et après désintégration

$$ $$E_system = 210 \\ p_system = 168 /c \uparrow$$

Ce qui, selon l'équation n ° 1 ', ramène la masse du système à $$$126 /c^2$ comme avec Petit, car

$$ $$210^2 = 168^2 + 126^2$$

L'observateur, du point de vue duquel Higgs se déplace vers la droite

Qu'avons-nous avec Bones? Kostya se déplace vers la gauche par rapport à Petya, par exemple, à une vitesse de v = 4/5 s, de sorte que Higgs (et Petya) se déplacent vers la droite par rapport à Kostya à une vitesse de v = 4/5 s. Les mêmes calculs que nous avons faits pour Masha montrent que l'énergie de Higgs $$$E_0 = 210 GeV et p_0 = 168 GeV$ mais, contrairement à Masha, pour qui Higgs se déplace vers le haut, pour Kostya, l'impulsion de Higgs est dirigée vers la droite. Ceci est illustré sur la fig. 10.


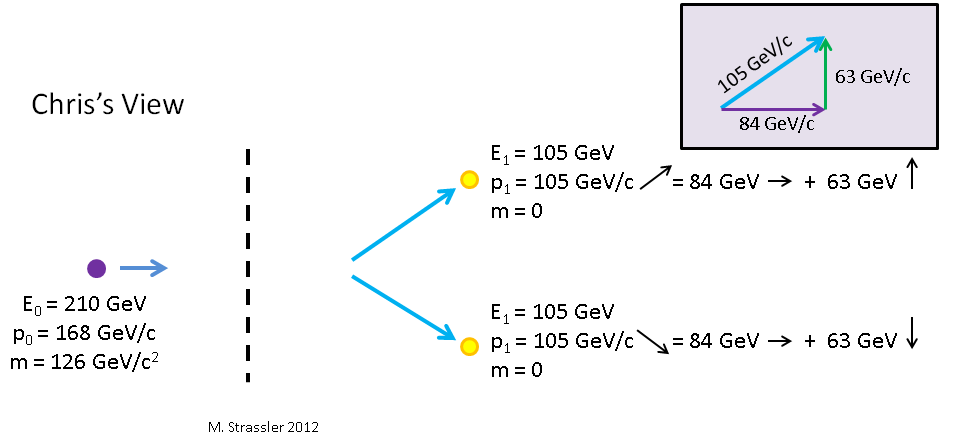
Fig. 10

Higgs se désintègre en deux photons. Si du point de vue de Petya les photons montent et descendent, alors pour Kostya, qui regarde Higgs et Petya se déplacer vers la droite, l'un des photons se déplace vers la droite et l'autre se déplace vers la droite. Quelle impulsion et quelle énergie auront-ils alors?

Par les équations n ° 4 et n ° 5, nous ne le savons pas, car elles sont destinées aux cas où la particule et l'observateur se déplacent dans la même direction. Pour notre cas, les équations seront les suivantes:

$$ $$\ updownarrow p = \ updownarrow \ overline p \\ \ leftrightarrow p = γ ([\ leftrightarrow \ overline p] + v \ overline E / c ^ 2) \\ E = γ (\ overline E + v [\ leftrightarrow \ overline p])$$

Ces équations seront plus simples qu'elles ne le paraissent, car du point de vue de Petit, p n'a pas de composante se déplaçant de gauche à droite, et toute l'impulsion monte ou descend. Kostya observe donc les valeurs suivantes pour Higgs:

$$ $$\ updownarrow p_0 = \ updownarrow \ overline p_0 = 0 \\ \ leftrightarrow p_0 = γ v \ overline {E_0} / c ^ 2 = (5/3) (4/5) 126 GeV / c = 168 GeV / c \ rightarrow \\ E = γ \ overline {E_0} = (5/3) 126 GeV = 210 GeV$$

Et le photon monte

$$ $$\ updownarrow p_0 = \ updownarrow \ overline p_1 = 63 GeV / c \ uparrow \\ \ leftrightarrow p_0 = γ v \ overline {E_1} = (5/3) (4/5) 63 GeV / c = 84 GeV / c \ rightarrow \\ E = γ \ overline {E_0} = (5/3) 63 GeV = 105 GeV$$

Pour le second photon, les formules sont les mêmes, seule sa composante verticale est dirigée vers le bas. Notez que pour les deux photons E = pc, selon le théorème de Pythagore pour la taille p pour chacune des impulsions, selon l'encart de la Fig. 10

$$ $$p_1 ^ 2 = (\ uparrow p_1) ^ 2 + (\ rightarrow p_1) ^ 2 \\ ou \\ (105 GeV / c) ^ 2 = (63 GeV / c) ^ 2 + (84 GeV / c) ^ 2$$

Et encore une fois, Kostya observe d'autres valeurs d'énergie et d'élan, en comparaison avec Petya et Masha. Mais pour Kostya, l'énergie et l'élan sont toujours conservés. Kostya observe également que la masse d'un système à deux photons coïncide avec la masse de Higgs. Pourquoi? La partie verticale totale de la quantité de mouvement du système est nulle, elle est mutuellement détruite. La partie horizontale de l'impulsion du système est de 168 GeV / s. L'énergie totale du système est de 210 GeV. C'est la même chose que Masha a observé, sauf que son élan du système a augmenté, et non vers la droite. Mais la direction de l'impulsion n'affecte pas l'équation n ° 1 '. Seule son ampleur y joue un rôle. Donc, comme Masha, Kostya voit que la masse du système de deux protons est $$ égale à la masse de la particule de Higgs primaire.

Résumé

Nous voyons donc ce que trois observateurs différents observent. Leurs observations:

• varient sur l'énergie et l'élan de Higgs,
• varient en termes d'énergie et de quantité de mouvement des deux photons,
• convenir de la conservation de l'énergie et de l'élan pendant la décroissance,
• par conséquent, ils conviennent que la masse du système est préservée,
• convient que la masse du système est de 126 GeV / c ² ,
• et de plus, que la somme des masses des objets du système n'est pas conservée, mais diminue de 126 GeV / c ² à zéro.

Et ce n'est pas un hasard. Einstein des expériences précédentes savait que l'énergie et l'élan sont conservés, il a donc cherché et trouvé des équations qui préservent cette caractéristique du monde. Toujours dans le processus, il a constaté que la masse du système doit satisfaire l'équation n ° 1 '.

Bonus: comment il est utilisé à la recherche d'une particule de Higgs

Scientifiques:

• observer les collisions de protons, à la suite desquelles naissent deux photons;
• calculer la masse d'un système de deux photons (dans le jargon technique, cela s'appelle la masse invariante d'une paire de photons).

Lorsque, à la suite d'une expérience, une particule de Higgs se désintègre en deux photons, quelle que soit la direction et la vitesse de déplacement de la particule par rapport au laboratoire, le système de deux photons dans lequel elle se désintègre aura toujours une masse égale à la masse Particules de Higgs qui les ont produites! Par conséquent, contrairement aux processus aléatoires, qui aboutissent à un système de deux photons de masse aléatoire, les particules de Higgs généreront toujours un système de deux photons de même masse. Par conséquent, si des particules de Higgs apparaissent dans les résultats de l'expérience, et si elles se désintègrent parfois en deux photons, alors nous verrons un pic de désintégrations de Higgs qui s'élève au-dessus du fond lisse d'autres processus aléatoires. Et c'est ce qui s'est passé dans l'expérience sur le LHC!