Le défi des cinq ans devenu "viral"

Toute la vérité sur le dernier puzzle de virus de Singapour et une autre énigme historique avec des chiffres



En l'honneur de l' anniversaire de cette chronique, Internet m'a gentiment fourni un problème mathématique singapourien devenu viral . À la mi-mai, le Web était ravi de la tâche que les élèves de première année de Singapour sont censés résoudre, qui sont des enfants âgés de 5 à 7 ans, et qui s'est avérée si difficile que personne ne peut la résoudre.


Étudiez soigneusement la séquence des nombres et remplissez les blancs

Mais notre histoire est en fait sur la façon dont des expressions comme «un problème mathématique a suscité Internet» sont devenues des tentatives ennuyeuses et prévisibles pour attirer les visiteurs sur la page. Étant donné que même un bref aperçu de ce problème, qui est apparu pour la première fois sur le forum technique de Singapour , nous permet de dire que cette photo est un faux évident. La photo semble modifiée, mais il n'y a aucune explication pour la tâche.

Apparemment, le puzzle a été tiré (et modifié) d'un site dédié aux puzzles mathématiques, dirigé par Gordon Burgin, un enseignant américain à la retraite. Et dans la version du site dans le quart inférieur gauche se trouve le numéro 20. Sur la photo de Singapour, 0 est taché. Pas étonnant qu'il n'y ait pas de solution évidente!

"Je suis étonné de ce faux et je ne sais pas ce qu'ils essayaient de réaliser", dit Burgin. "Si leur objectif était une discussion animée et le désespoir qui a suivi, ils ont atteint leur objectif!"

Vient ensuite le casse-tête correct.

1. Dans chacun des quatre secteurs du cercle extérieur, il y a un nombre à deux chiffres égal à la somme des trois nombres situés dans les coins de ce secteur. Les nombres dans les cercles individuels peuvent varier de 1 à 9, et chacun des nombres ne peut être utilisé qu'une seule fois. Un des numéros vous est donné pour commencer. Trouvez les quatre autres.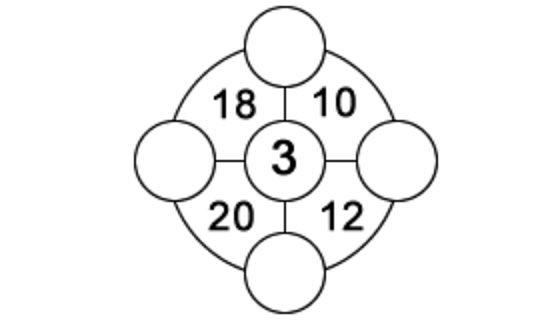



2. Puisque l'énigme de Singapour était incorrecte - essayez de proposer une variante du problème qui conviendrait à l'image donnée (avec une remise à zéro).

Cette énigme m'a rappelé un puzzle d'un des livres les plus intéressants sur l'histoire des énigmes: " Wakoku chiekurabe ", le plus ancien livre d'énigmes japonais, publié en 1727. C'est un merveilleux mystère - et au moins elle vient de naître en Orient!

3. Notez les nombres de 1 à 9 dans des cercles noirs afin que la somme des nombres situés sur chacun des deux cercles bleus (y compris le cercle central), ainsi que le long des lignes horizontales et verticales, soit la même.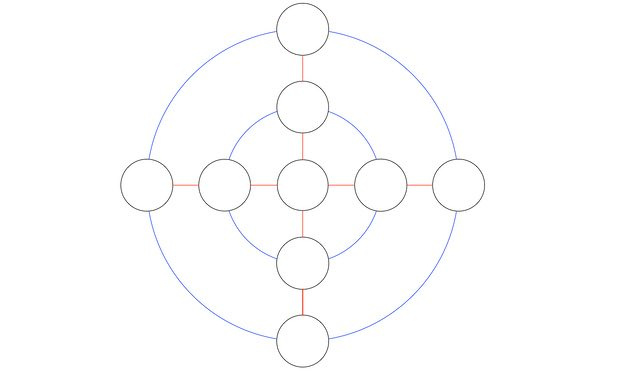



Ce sont quatre montants, chacun composé de cinq termes, et tous les montants sont les mêmes. Voici une image tirée du livre lui-même, qui représente une tâche similaire.

Des solutions

1. Dans le sens horaire, en partant du haut: 6, 1, 8, 9

Si nous nommons les positions pour les nombres Nord, Est, Ouest et Sud, alors les candidats pour l'Ouest et le Sud seront 8 et 9, puisque S + 3 + 3 = 20, ou S + 3 = 17. Mais nous savons que S + B + 3 = 12, ou 10 + B = 9. Mais 10 ne peut pas être 9, car alors B = 0, et cela est interdit. Par conséquent, = = 8, 3 = 9, C = 6 et B = 1.

2. Ce que j'ai le plus aimé, c'est le devoir envoyé par un lecteur nommé Tom Flannery, car il s'est avéré très simple.

Remplissez les cercles avec des nombres entiers de sorte que la somme des secteurs dans chacun des demi-cercles soit égale à la somme des nombres dans les cercles.

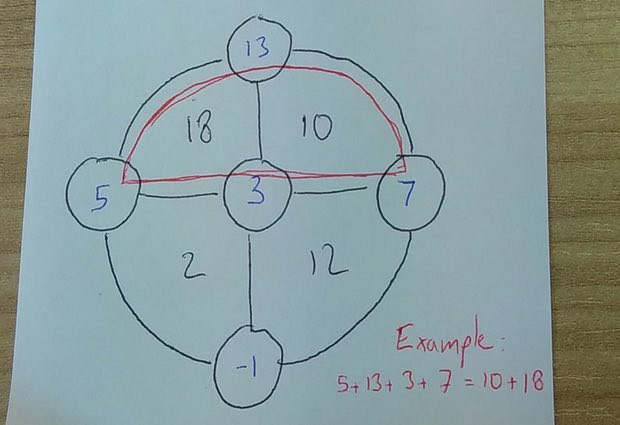
3. Et la dernière tâche, de la collection japonaise d'énigmes de 1727.

Il peut y avoir de nombreuses solutions. Voici ma solution:



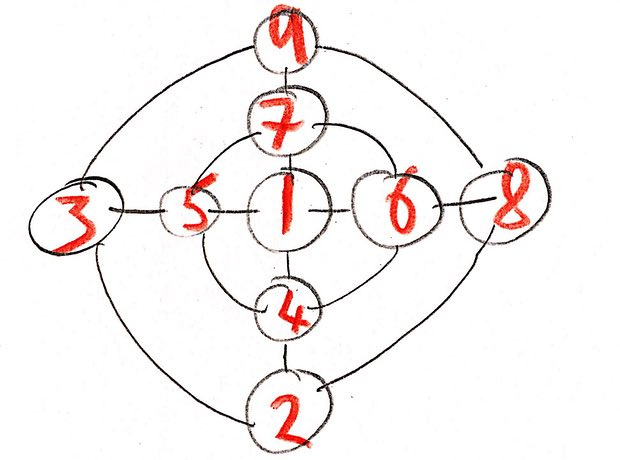
Le chemin vers la solution nous aide à deviner - au centre, il ne peut y avoir qu'un nombre impair. Après avoir choisi un tel nombre, vous devez diviser les chiffres restants en paires qui totalisent le même nombre et les disposer dans des cercles opposés. J'ai choisi 1 pour le centre, respectivement, il y a les paires 2 et 9, 3 et 8, 4 et 7, 5 et 6 - tous donnent un total de 11.