Particules, antiparticules et leur annihilation

Les antiparticules sont souvent présentées plus mystiques et mystérieuses qu'elles ne le sont réellement, et tout cela grâce à la science-fiction et à d'autres œuvres, comme « Angels and Demons » de Dan Brown.

Chaque type de particule a une antiparticule. Il s'agit généralement d'une particule distincte, mais il arrive que l'antiparticule et la particule soient une seule et même chose. Seules les particules qui remplissent certaines conditions (par exemple, électriquement neutres) peuvent être des antiparticules de leur propre gré. Une petite liste d'exemples de telles particules sont les photons, les particules Z, les gluons et les gravitons. Peut-être trois neutrinos. Toutes les autres particules ont des antiparticules distinctes qui ont la même masse mais la charge électrique opposée. Un neutron est un exemple de particule électriquement neutre qui n'est pas une antiparticule en soi. Comme un proton, un neutron a plus de quarks que d'antiquarks, et un antineutron a plus d'antiquarks que de quarks.

Pour les particules autres que les antiparticules, les noms des antiparticules sont généralement assez évidents (antiquark supérieur, antineutrino, antitau), à l'exception de l'antielectron, qui est généralement appelé positron.

Pourquoi l'antimatière est-elle si célèbre, pourquoi sonne-t-elle si mystérieuse? Tout cela grâce à la déclaration «la matière et l'antimatière s'anéantissent en énergie pure». Cette déclaration semble cool, mais ce n'est pas grave. Ce n'est pas tout à fait faux, mais ce n'est pas vrai non plus. La réalité est plus complexe et pas si surprenante.

Par souci de simplicité, les physiciens omettent souvent le préfixe «anti», lorsqu'il apparaît clairement dans le contexte. Exemples:

• Dans de nombreux processus, le muon et l'antimuon apparaissent. Les physiciens appellent parfois cela la «paire de muons».
• Une particule W se désintègre en un quark supérieur et un antiquark inférieur, et on dit souvent qu'elle se désintègre «en quarks».

Annihilation des particules et des antiparticules

L'anéantissement des particules et des antiparticules consacre beaucoup de matériaux - cela semble mystérieux, effrayant et fantastique - mais ce sont les principaux processus qui se déroulent au cœur de la physique des particules, et une telle description conduit à de fréquents malentendus. Je veux décrire quelques règles de base qui déterminent si une particule et une antiparticule d'un type se transforment en une autre paire de particules et d'antiparticules, s'approchant les unes des autres. Ce n'est pas une histoire complète d'anéantissement des particules et des antiparticules, mais un bon début.

Dans un monde comme le nôtre, contrôlé par la mécanique quantique et la relativité d'Einstein, il existe un théorème mathématique: pour chaque type de particule, il existe un type d'antiparticule correspondant avec exactement la même masse. Ce n'est pas seulement un théorème - pour toutes les particules connues, les antiparticules ont été obtenues expérimentalement, il n'y a donc rien à contester.

Cependant, certaines particules coïncident avec des antiparticules: l'antiparticule d'un photon (particules de lumière) sera un photon. Il en sera de même pour la particule Z et la particule de Higgs. En revanche, un électron à charge électrique négative (par définition) possède une antiparticule, anti-électronique ou positron, à charge positive. Presque toutes les particules connues ont ceci: un muon a un antimuon, un quark supérieur a un antiquark supérieur, une particule W avec une charge positive a une antiparticule W avec une négative.

Si vous réunissez une particule et une antiparticule, presque toutes leurs propriétés sont mutuellement détruites. Par exemple, la charge électrique d'un muon (un cousin lourd d'un électron) plus la charge électrique d'un antimuon sera nulle. Le premier est négatif, le second est positif, mais ils sont de taille égale. La seule chose qui n'est pas détruite est leur masse et leur énergie. Certes, cette déclaration est une petite astuce. La masse n'est pas «conservée» - elle peut apparaître et disparaître , ce qui est très bon pour la physique des particules. La seule chose qui n'ira nulle part est l'énergie. L'énergie est économisée: avec laquelle vous avez commencé, vous finirez avec cela.

1. Muon et antimuon se transforment en deux photons

Supposons que j'ai une boîte à chaussures dans laquelle il n'y a que le muon et l'antimuon qui sont pratiquement au repos. Ensuite, l'énergie à l'intérieur de la boîte est égale à l'énergie de la masse du muon et à l'énergie de la masse de l'antimuon. ["Pratiquement" - parce que j'omet le champ électrique entre le muon et l'antimuon, mais c'est un effet très minuscule qui peut être ignoré dans notre cas.] Supposons que la masse du muon soit M, alors l'énergie de la masse du muon sera M c ² , et la même chose sera vrai pour l'antimuon. Les impulsions des deux particules seront nulles, car elles ne bougent pas. L'énergie totale E et la quantité de mouvement p dans la boîte sont initialement

$$

$$E_ {initial} = 2 M c ^ 2 \\ p_ {initial} = 0$$

Tout le reste dans la boîte est nul: la charge électrique totale, le moment angulaire, etc. Seulement de l'énergie. Et la masse - mais ils sont liés les uns aux autres.

Puisque presque tout est annihilé mutuellement, la particule et l'antiparticule peuvent se transformer par l'une des quatre interactions connues en une autre particule et son antiparticule. Par exemple, un muon et un antimuon peuvent se transformer en photon et en second photon (rappelez-vous, le photon est lui-même une antiparticule). Les deux photons auront de l'énergie - mais combien? Eh bien, les photons seront les mêmes, et ils auront la même énergie, et puisqu'il est stocké, l'énergie finale totale sera la même que l'initiale totale:

$$

$$E_ {photon} = 1/2 E_ {final} = 1/2 E_ {initial} = M c ^ 2 = E_ {muon}$$

Faites attention à ce qui vient de se passer: nous avons commencé avec des particules massives, chacune ne se déplaçant pas, et n'ayant pas l'énergie du mouvement, mais elle avait l'énergie de la masse M c ² . Et nous nous sommes retrouvés avec deux particules sans masse, sans énergie de masse, mais avec une énergie de mouvement égale à l'énergie de masse des muons:
M c ² . Voir fig. 1.


Fig. 1

De plus, les photons auront des impulsions. Mais les impulsions des deux photons seront dirigées de façon opposée et détruites mutuellement, de sorte que l'impulsion totale sera nulle.

$$

$$p_ {final} = p_ {initial} = 0$$

Notez que l'énergie est conservée, l'élan est conservé, mais pas la masse. La masse résultante est nulle, bien que la masse initiale soit de 2 M.

2. Le muon et l'antimuon se transforment en un électron et un anti-électron

Réaction simple:

$$

$$particule_1 + antiparticule_1 \ rightarrow particule_2 + antiparticule_2$$

non seulement un processus possible pour anéantir une particule et une antiparticule, mais aussi très courant. Examinons une autre option pour la particule 2.


Fig. 2

Au lieu de devenir deux photons, le muon et l'antimuon peuvent se transformer en un électron et un positron (anti-électron), comme sur la Fig. 2. Les deux auront la même masse; appelons-la m. La masse d'un électron est environ 200 fois inférieure à la masse du muon M. Ce que le muon et l'antimuon transformeront en photons ou en une paire électron / positron détermine le caractère aléatoire, mais avec la probabilité décrite par les équations de la mécanique quantique.

La même logique que précédemment nous conduit à la même conclusion. Nous aurons une symétrie, un électron et un positron, avec la même masse, la même énergie, et grâce à la loi de conservation, l'énergie totale devrait être la même que l'énergie initiale du muon.

$$

$$E_ {électron} = E_ {positron} = 1/2 E_ {final} = 1/2 E_ {initial} = M c2 = E_ {muon}$$

La situation est un peu différente: nous avons commencé avec des particules immobiles massives qui n'ont pas d'énergie de mouvement et ont une énergie de masse M c ² . Et nous avons terminé avec deux particules massives, chacune ayant une énergie de masse mc ² et beaucoup d'énergie de mouvement, et l'énergie totale d'un électron est égale à l'énergie de la masse du muon M c ² . Encore une fois, l'impulsion électronique est mutuellement détruite avec l'impulsion positron:

$$

$$p_ {final} = 0$$

Bien sûr, leurs charges électriques sont mutuellement détruites. Il n'y avait aucun frais dans la boîte avant la transformation, il n'y en a pas après. L'énergie est à nouveau conservée, l'élan est conservé, la charge est conservée, mais la masse ne l'est pas. La masse initiale était de 2M et la masse finale était de 2m.


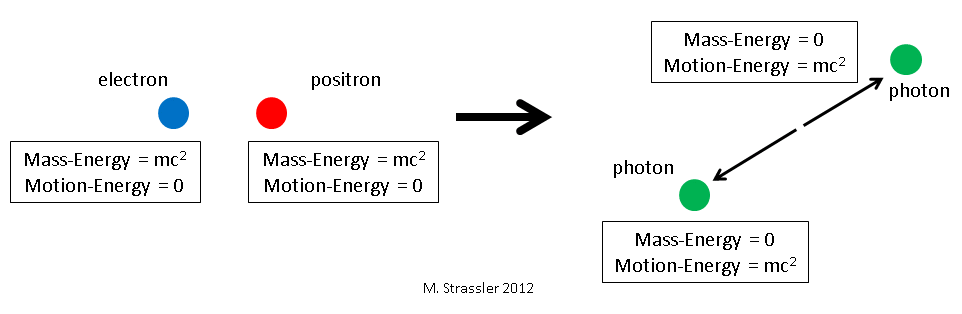Fig. 3

3. L'électron et l'antiélectron se transforment en deux photons

Un électron au repos et un positron peuvent se transformer en deux photons, tout comme un muon et un antimuon. Tous les calculs peuvent être effectués, réduisant le problème au cas des muons, remplaçant simplement M partout par m. Il n'y a pas de différence (comparer Fig.1 et Fig.3).

4. Un électron et un antiélectron peuvent-ils se transformer en muon et antimuon?

Non et oui. La réponse dépend de la question:

• Non, si l'électron et le positron sont initialement au repos. Ils n'ont pas assez d'énergie pour créer un muon et un antimuon, donc ce processus ne se produira pas.
• Oui, si l'électron et le positron ont des énergies de mouvement élevées et entrent en collision très fortement. Un processus peut se produire tant qu'ils ont suffisamment d'énergie.

Tout d'abord, assurons-nous que si l'électron et le positron sont au repos - ils n'ont pas l'énergie du mouvement - ils ne pourront pas se transformer en muon et antimuon. La logique est simple - il suffit de revenir au problème précédent, dans lequel le muon et l'antimuon étaient transformés en un électron et un positron, et partout où nous remplaçons le muon par un électron, l'antimuon par un positron, M par m. Il se révélera:

$$

$$E_ {muon} = E_ {antimuon} = 1/2 E_ {final} = 1/2 E_ {initial} = m c ^ 2 = E_ {électron}$$

Mais c'est impossible! Le muon a une énergie de masse M c ² , plus une énergie positive de mouvement. M> m. Il s'avère une contradiction:

$$

$$E_ {muon} = M c ^ 2 + "énergie de mouvement" ≥ M c ^ 2> m c ^ 2$$

L'énergie muonique ne peut pas être égale à mc ² , comme l'exige la conservation de l'énergie, puisque M> m. Il faut admettre que ce processus ne peut pas se produire.


Fig. 4

Cependant, c'est précisément pourquoi cette tentative ne fonctionne pas et nous indique comment réaliser ce que nous voulons. Pas besoin de considérer l'électron et le positron au repos. Accélérons-les - presque à la vitesse de la lumière, afin que leur énergie de mouvement devienne très grande et que l'énergie totale (énergie de masse et énergie de mouvement) soit sensiblement supérieure à mc ² . Pour simplifier, imaginons que leur énergie initiale soit devenue égale à M c ² . Ensuite, l'énergie initiale totale dans la boîte sera de 2 M c ² , et pour que le processus se déroule, la loi de conservation exige:

$$

$$E_ {muon} = E_ {antimuon} = 1/2 E_ {final} = 1/2 E_ {initial} = M c2 = E_ {électron}$$

Ce qui ne contredit pas les exigences de l'équation précédente

$$

$$E_ {muon} = M c ^ 2 + "énergie de mouvement" ≥ M c ^ 2> m c ^ 2$$

L'énergie de l'électron et du positron est à peine suffisante pour créer le muon et l'antimuon au repos (Fig. 5).


Fig. 5

Si nous rendons l'énergie de l'électron et du positron encore plus grande, nous pouvons créer le muon et l'antimuon. L'excès d'énergie se transformera en énergie de mouvement du muon et de l'antimuon, voir Fig. 6.

Notez que la masse n'est pas conservée à nouveau, bien que l'énergie soit conservée. Dans ce cas, la masse a augmenté, passant de 2m à 2M. C'est très important pour la physique des particules! C'est l'une des principales techniques que nous utilisons pour découvrir de nouvelles particules. Nous heurtons la particule et l'antiparticule avec de très grandes énergies de mouvement, en espérant qu'elles se transformeront en une particule lourde, sans précédent auparavant, avec son antiparticule.


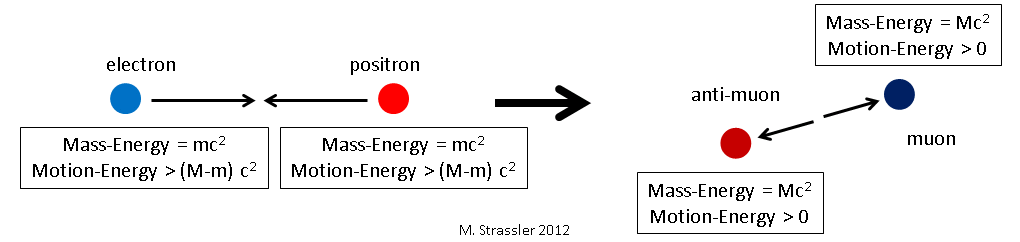Fig. 6

Résumé

• Une particule stationnaire et son antiparticule peuvent s'annihiler, donnant naissance à une particule et une antiparticule, si la particule initiale est plus lourde que la dernière.
• Une particule et une antiparticule stationnaires ne peuvent pas s'annihiler, donnant naissance à une particule et une antiparticule si la particule finale est plus lourde que la particule initiale.
• Une particule se déplaçant les unes par rapport aux autres et ses antiparticules peuvent s'annihiler, donnant naissance à une particule et une antiparticule plus lourdes si elles ont suffisamment d'énergie de mouvement.
• Si la somme de l'énergie de masse et de l'énergie de mouvement des particules est égale à l'énergie de masse d'une particule plus lourde, alors la particule lourde et l'antiparticule résultantes seront immobiles.
• Si la somme de l'énergie de la masse et de l'énergie du mouvement des particules est supérieure à l'énergie de masse de la particule plus lourde, alors l'excès d'énergie se transformera en énergie de mouvement des particules et antiparticules plus lourdes.