Les mathématiques nous donnent une image précise des réponses presque exactes.

À l'aide de papier épais et de ruban transparent, Craig Kaplan recueille un bel objet arrondi ressemblant à la création de
Buckminster Fuller ou d'un nouveau type de ballon de football à la mode. Il se compose de quatre dodécagones réguliers (12 gons avec les mêmes angles et côtés) et 12 décagones (polyèdres à 10 côtés) avec 28 petites ouvertures en forme de triangles équilatéraux. Il n'y a qu'un seul problème - ce chiffre ne peut pas exister. Un tel ensemble de polygones ne coïncide pas avec les sommets et la figure ne se ferme pas.
Le modèle Kaplan ne fonctionne que parce que lorsque vous l'assemblez à partir de papier, vous avez peu de liberté de manœuvre. Les côtés peuvent se plier presque imperceptiblement. «La marge d'erreur résultant du travail dans le monde réel avec du papier signifie que des choses qui ne devraient pas être possibles sont réellement obtenues», explique Kaplan, informaticien à l'Université de Waterloo au Canada.

Il s'agit d'un nouvel exemple d'une classe d'objets mathématiques inattendus sur laquelle le mathématicien américain Norman Johnson est tombé dans les années 1960. Johnson a travaillé à l'achèvement d'un projet commencé il y a plus de 2000 ans par Platon - il a créé un catalogue de formes géométriques idéales. Sur l'infinie variété de figures tridimensionnelles, seules
cinq peuvent être créées à partir des mêmes polygones réguliers: tétraèdre, octaèdre, hexaèdre, icosaèdre, dodécaèdre. Si vous mélangez différents polygones réguliers, vous pouvez composer 13 figures supplémentaires dans lesquelles tous les polygones rencontrent des sommets -
corps archimédiens - ainsi que des prismes (deux polygones identiques reliés par des carrés) et des «antiprismes» (deux polygones identiques reliés par des triangles équilatéraux).
En 1966, Johnson, alors qu'il travaillait à l'Université du Michigan, a découvert 92 autres corps composés uniquement de polygones réguliers, qui sont maintenant [aux États-Unis] appelés
corps Johnson . Et cela a épuisé toutes les possibilités, ce qui a été prouvé plusieurs années plus tard par le mathématicien russe
Viktor Abramovich Zalgaller , qui a ensuite travaillé à l'Université d'État de Leningrad. Il est impossible de créer une autre forme fermée à partir de polygones réguliers.
Mais lors d'un inventaire des polyèdres, Johnson a remarqué quelque chose d'étrange. Il a trouvé ses formes, composant leurs modèles à partir de cartons et de bandes élastiques. Puisqu'il y a assez peu de polyèdres possibles, il s'attendait à ce que de nouvelles formes apparaissent assez rapidement. Si vous commencez à faire des grimaces ensemble, la figure doit nécessairement coïncider. Mais cela ne s'est pas produit. «Lors de l'assemblage d'un tas de polygones, il n'était pas toujours évident de savoir si j'avais assemblé une forme valide», se souvient Johnson.
Il peut sembler que le modèle s'est assemblé, mais «si vous faites les calculs, il s'avère que ce n'est pas entièrement vrai», dit-il. Après un examen attentif, il s'est avéré que ce qui semblait être un carré n'était pas tout à fait un carré, ou que les côtés n'étaient pas tout à fait plats. Il serait possible d'ajuster légèrement les faces, et elles s'ajusteraient parfaitement, mais alors elles ne seraient plus des polygones réguliers.
Dans l'intention de calculer tous les chiffres idéaux, Johnson n'a pas attaché d'importance à de tels «coups rapprochés». «Je les ai mis de côté et je me suis concentré sur l'acceptable», dit-il. Mais ces chiffres presque idéaux ont non seulement attiré l'attention de Kaplan et d'autres amateurs de mathématiques, mais ils sont devenus une partie d'une plus grande section de mathématiques presque idéales.
Il n'y a pas de définition exacte d'un hit «presque précis». Des règles strictes ne fonctionnent pas dans un monde tolérant. Maintenant, Kaplan est guidé par une méthode approximative dans la recherche de figures presque correctes: "une erreur mathématique réelle inhérente à une figure est comparable à une erreur pratique résultant du travail avec des matériaux du monde réel et des mains imparfaites" En d'autres termes, si vous avez réussi à assembler un polyèdre impossible - s'il est si proche du possible que vous pouvez le faire passer pour un vrai - alors ce sera un chiffre presque exact. Dans d'autres branches des mathématiques, des résultats presque précis sont si proches du réel qu'ils peuvent vous tromper ou vous surprendre - une sorte de blague mathématique.
Certaines de ces bizarreries mathématiques ne peuvent être qualifiées de plus que de simples amusements, tandis que d'autres peuvent avoir des significations profondes en mathématiques et en physique.
Les anciens problèmes de
quadrature d'un cercle et de
doublement d'un cube entrent dans la catégorie des solutions presque correctes. Ils semblent tentants de trouver la bonne solution, mais au final, ils s'avèrent impossibles - comme une figure géométrique qui semble fermée mais ne l'est pas. Certains dessins dessinés par Léonard de Vinci et Albrecht Durer ont légèrement plié les coins, donnant des pentagones presque réguliers comme de vrais.
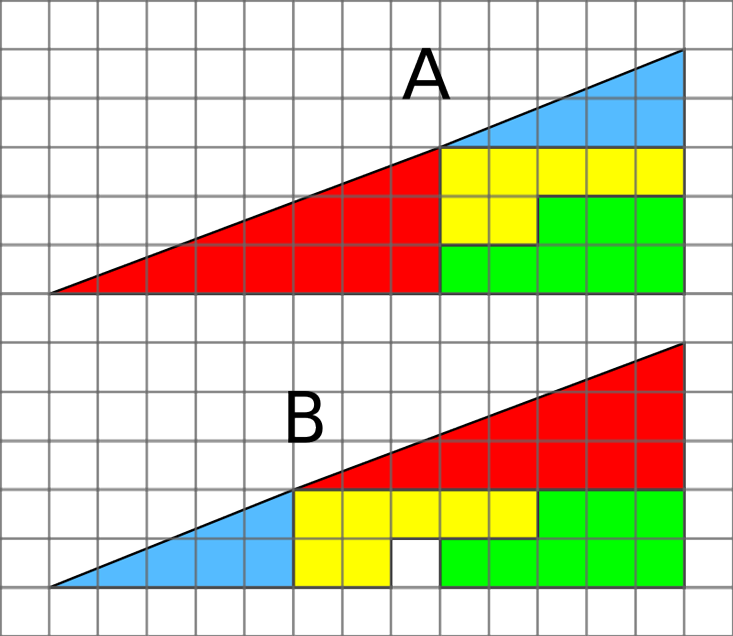
Et il y a une énigme avec un carré manquant. Dans la figure, un triangle rectangle est coupé en quatre parties. Si vous les réorganisez, un espace apparaît. D'où venait-il? C'est aussi presque la bonne décision. Aucun des triangles n'est en fait un triangle. Leurs hypoténuses sont tordues, et il est presque impossible de le remarquer, c'est pourquoi l'illusion est si convaincante.
L'appariement numérique est l'une des décisions presque à droite les plus utiles dans la vie quotidienne. 2
7/12 est presque égal à 3/2. Pour une raison similaire, le piano a 12 touches dans une octave et au cœur du
système uniformément tempéré de la musique occidentale. Il s'agit d'un compromis entre les deux intervalles musicaux les plus importants: une octave (fréquence 2: 1) et une cinquième (fréquence 3: 2). Numériquement, il n'est pas possible de diviser une octave pour que tous les cinquièmes soient parfaits. Mais vous pouvez vous en approcher suffisamment en divisant l'octave en 12 demi-tons, dont sept vous donnera une fréquence de 1,498. Pour la plupart des gens, cela suffit.
Parfois, des résultats presque exacts se produisent en mathématiques comme s'ils se trompaient. Dans l'épisode Simpsons "Treehouse of Horror VI", le public intéressé par les mathématiques a remarqué quelque chose d'inhabituel: équation 1782
12 + 1841
12 = 1922
12 . À première vue, il pourrait sembler que les auteurs ont réfuté le grand théorème de Fermat, en postulant que l'équation x
n + y
n = z
n n'a pas de solutions entières pour n> 2. Si vous entrez ces nombres dans une calculatrice de poche, le résultat semblera correct. Mais si vous effectuez des calculs avec une précision non disponible pour la plupart des calculatrices de poche, il s'avère que la racine du 12e degré à partir du côté gauche de l'équation est 1921,9999999555567 et non 1922, et Fermat peut être calme. Étonnamment petit glissement - moins de 10 millions de pièces.
Mais ces succès presque précis ne sont pas que des blagues. «Ceux qui m'intriguent plus que d'autres sont des cas qui font allusion à la présence de quelque chose de plus important», explique John Baez, mathématicien à l'Université de Californie à Riverside. C'est le cas d'une quantité qui est parfois appelée la constante de
Ramanujan . Ce nombre e
π √163 , égal à environ 262 537 412 640 768 743.9999999999999925, est étonnamment proche de l'ensemble. Nous ne pouvons pas nous attendre à ce que ces trois nombres irrationnels - e, π et √163 - se combinent et nous donnent un nombre rationnel, sans parler du tout. Mais il y a une raison pour laquelle ils correspondent si bien. «Ce n'est pas seulement une coïncidence dont nous n'avons aucune idée», explique Baez. "C'est la clé des profondeurs des mathématiques." L'explication exacte est assez compliquée, mais basée sur le fait que 163 est le plus grand
nombre de Hegner . Les exposants associés à ces nombres sont très proches d'entiers.
Ou prenez une connexion mathématique connue sous le nom d '«hypothèse de monstrueux clair de lune» (monstrous moonshine). L'histoire est la suivante: en 1978, le mathématicien John Mackay a fait à quel point l'observation était banale, tout aussi intéressante: 196 884 = 196 883 + 1. Le premier nombre était un coefficient d'un polynôme important,
invariant j , et le second est apparu en rapport avec un énorme objet mathématique de la théorie des groupes appelé "
Monster ". Beaucoup de gens haussaient les épaules et allaient plus loin, mais cette observation a intéressé de nombreux mathématiciens qui ont décidé de l'étudier de plus près. Ils ont trouvé un lien entre deux sujets apparemment sans rapport: la théorie des nombres et la symétrie des groupes Monster. Cette connexion peut avoir des conséquences encore plus larges, pas encore ouvertes pour d'autres sujets. Le physicien Edward Whitten pense que le groupe Monster peut être associé à la gravité quantique et à la structure espace-temps.
Les succès mathématiques presque corrects montrent à la fois le caractère ludique et la puissance de l'approche humaine des mathématiques. Johnson, Kaplan et d'autres ont fait des découvertes par essais et erreurs - étudiant le domaine en tant que biologiste se promenant dans la jungle à la recherche de nouvelles espèces. Mais en mathématiques, il est plus facile d'effectuer une recherche systématique. Par exemple, Jim McNeill, qui s'intéresse aux mathématiques comme passe-temps et recueille une collection de hits presque corrects sur son site, et Robert Webb, un programmeur, a créé un logiciel pour créer et étudier les polyèdres.
Des hits presque précis vivent sur la ligne floue entre les mathématiques idéalistes et dures et nos sentiments condescendants et pratiques. Ils renversent la logique de l'approximation. Habituellement, le monde réel est considéré comme une ombre imparfaite du monde de Platon. La perfection des mathématiques sous-jacentes est perdue dans sa mise en œuvre. Mais dans le cas de hits presque précis, le monde réel est l'ombre parfaite du monde imparfait. L'approximation est «la mauvaise approximation de la bonne réponse», dit Kaplan, et «un résultat presque précis est une représentation exacte d'une réponse presque exacte».
De cette façon, des réponses presque précises changent le lien entre les mathématiciens et les physiciens mathématiques avec la nature. «Je suis reconnaissant des imperfections du monde réel, car elles me permettent d'atteindre un quasi-idéal en travaillant avec des objets qui sont essentiellement imparfaits», explique Kaplan. «Ils me permettent de surmonter les limites des mathématiques grâce à la beauté d'une réalité brisée.»