Le fait que beaucoup de ceux qui étudient la nature de la matière ordinaire pour la première fois sont déconcertés est que le noyau de tout atome est plus lourd que l'hydrogène contient à la fois des protons et des neutrons, mais en même temps, les neutrons se désintègrent (se désintègrent en d'autres particules) en moyenne 15 minutes! Comment les noyaux de carbone, d'oxygène, d'azote, de silicium peuvent-ils être aussi stables si les neutrons qui les composent ne peuvent survivre par eux-mêmes?
La réponse à cette question se révèle très simple une fois que vous comprenez comment fonctionne l'énergie: c'est de la pure comptabilité. Mais comprendre l'énergie est loin d'être facile. Vous devez d'abord lire
un article sur les types d'énergie . Avant cela, vous devez lire l'
article sur l'énergie, l'élan et la masse . Ces concepts doivent être présentés avant de comprendre la réponse à la question.
Si vous lisez un article sur l'énergie d'interaction, vous savez qu'un atome d'hydrogène se compose d'un proton et d'un électron qui, en raison de l'énergie de liaison négative, ne peuvent pas s'échapper l'un de l'autre - ils sont enfermés à l'intérieur de l'atome. L'énergie de liaison négative provient de l'énergie d'interaction négative, partiellement équilibrée par l'énergie positive de mouvement de l'électron (et un peu - le proton). L'énergie d'interaction provient de l'action d'un électron sur un champ électrique près d'un proton (et vice versa).
Dans cet article, j'expliquerai pourquoi un neutron est stable dans le prochain noyau atomique le plus simple: un deutéron, un noyau "d'hydrogène lourd" ou "deutérium". Un deutéron se compose d'un neutron et d'un proton - en principe, il est simple et pas trop différent d'un atome d'hydrogène avec un électron et un proton. Comprendre pourquoi un neutron est stable dans un deutéron, vous comprendrez le principe de base selon lequel les neutrons peuvent être stables à l'intérieur de tous les noyaux stables. L'essentiel est: l'énergie d'interaction des protons et des neutrons est négative, et assez grande, par conséquent, dans certains noyaux, la désintégration d'un neutron entraînerait une augmentation de l'énergie du système (constituée du reste du noyau après sa désintégration et de toutes les particules émises pendant la désintégration), ce qui violerait la loi de conservation de l'énergie. Puisque l'énergie doit être conservée, la décroissance n'est pas possible.
Je ne décrirai pas l'interaction d'un neutron avec un proton, car une forte interaction en est responsable, beaucoup plus complexe que les interactions électriques (et magnétiques) entre un proton et un électron qui composent un atome d'hydrogène. Une partie de cette complexité est due à la nature composite de l'interaction - c'est un peu comme l'interaction électromagnétique peut lier deux atomes d'hydrogène en une molécule d'hydrogène, bien que les deux atomes soient électriquement neutres. Mais certains détails importants ne sont pas couverts par cette analogie. La physique nucléaire est une question distincte.
Fig. 1Heureusement, nous n'avons pas besoin de ces difficultés. Nous devons savoir que ces forces créent une énergie d'interaction négative pour un système de protons, de neutrons et de divers champs complexes, leur permettant de s'influencer mutuellement. Le résultat est un deutéron stable. Tout comme un atome d'hydrogène ne peut pas subitement se désintégrer en un électron et un proton, un deutéron ne peut pas subitement se désintégrer en un neutron et un proton.
Cela ne signifie pas qu'un deutéron ou un atome d'hydrogène ne peut pas être détruit. Vous pouvez «ioniser» un atome d'hydrogène (assommer un électron sur un proton) si vous ajoutez de l'énergie externe - sous la forme, par exemple, d'un photon assez énergétique. La même méthode peut être utilisée pour briser le deutérium et éliminer un neutron sur un proton. Mais l'énergie pour cela doit être obtenue en dehors du système; ni l'hydrogène ni le deutéron ne se décomposeront d'eux-mêmes.
Le neutron peut se désintégrer
Rappelons la condition nécessaire (mais non suffisante) à la désintégration d'un objet - la masse de l'objet initial doit dépasser la somme des masses des objets dans lesquels il se désintègre. D'où vient cette condition? De la loi de conservation de l'énergie. Bientôt, nous verrons comment et pourquoi (comme d'habitude, je veux dire par "masse de paix").
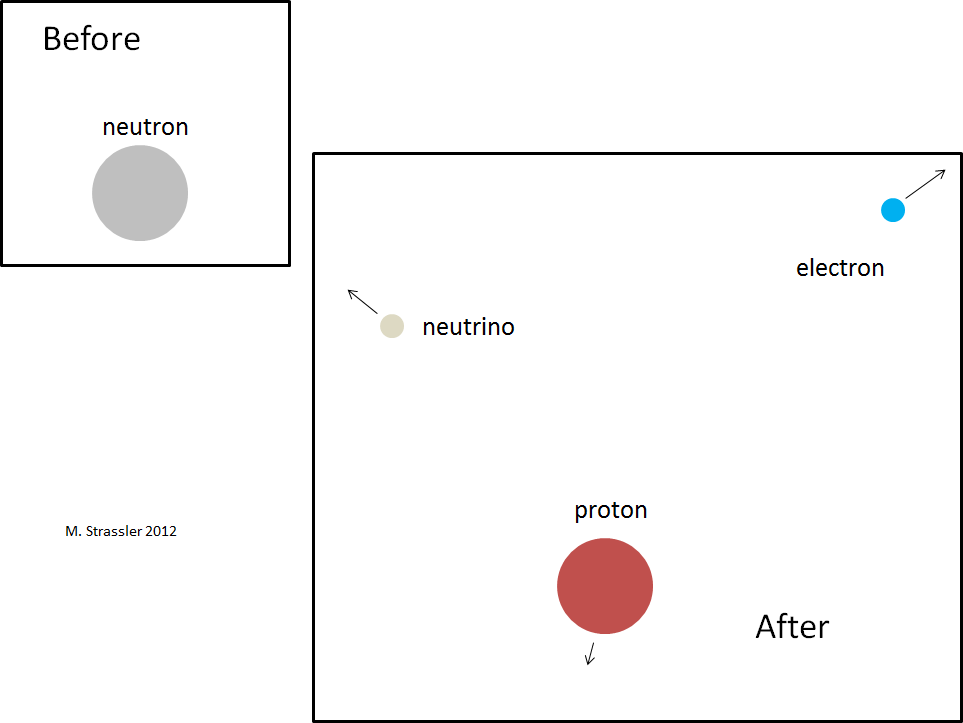Fig. 2Vérifions que cette condition est remplie pour un neutron, qui peut se désintégrer en proton, électron et antineutrino électronique. La décomposition est illustrée à la figure 2; le neutron se transforme spontanément en ces trois particules. Le neutron et le proton sont en réalité plus gros que l'électron et l'antineutrino - bien que l'image ne soit toujours pas dessinée à l'échelle. Le diamètre d'un neutron ou d'un proton est d'environ un milliardième de trillionième de mètre (100 000 fois plus petit qu'un atome), et environ le diamètre d'un électron ou d'un neutrino, il est connu qu'il est au moins 1000 fois plus petit que cela.
Dans la fig. 3 représente la comptabilité énergétique (voir Fig. 1). Avant la désintégration des neutrons, l'énergie de l'ensemble du système est égale à l'énergie de masse (E = mc
2 ) du neutron. La masse neutronique est de 0,939565 ... GeV / c
2 .
Les points de suspension indiquent qu'il ne s'agit pas d'une valeur exacte, mais jusqu'à présent, nous n'avons pas besoin de plus de précision. Par conséquent, l'énergie de la masse neutronique
0,939565 ... GeV / c
2Après la désintégration des neutrons, quelle sera l'énergie de l'ensemble du système? Puisque l'énergie est conservée, mais qu'aucune énergie n'a été fournie de l'extérieur, l'énergie du système sera la même - 0,939565 ... GeV!
Mais comment est-il distribué?
Premièrement, nous n'aurons pas l'énergie d'interaction. Ce n'est pas évident, mais très important. Lorsqu'un proton, un électron et un antineutrino se séparent, l'énergie de leur interaction devient négligeable.
Deuxièmement, chacune des particules a une énergie de masse. Combien y en a-t-il?
• L'énergie massique du proton est de 0,938272 ... GeV.
• L'énergie de la masse électronique est de 0,000511 ... GeV.
• L'énergie de la masse antineutrino peut être négligée, elle est si petite.
Et c'est bien, car la masse de neutrinos ne nous est pas encore connue. Nous savons qu'elle est au moins bien inférieure à 0,000001 GeV.
La masse-énergie résultante est égale à
(0,938272 ... + 0,000511 ... + 0,000000 ...) GeV = 0,938783 ... GeV
Ce qui est inférieur à l'énergie de masse du neutron avec lequel nous avons commencé, par 0,000782 ... GeV. Jusqu'à présent, nous ne voyons pas comment il est conservé. L'énergie de masse d'un neutron ne s'est pas complètement transformée en énergie de masse d'un proton, d'un électron et d'un neutrino. L'excès d'énergie dans la Fig. 3 sont représentés en jaune.
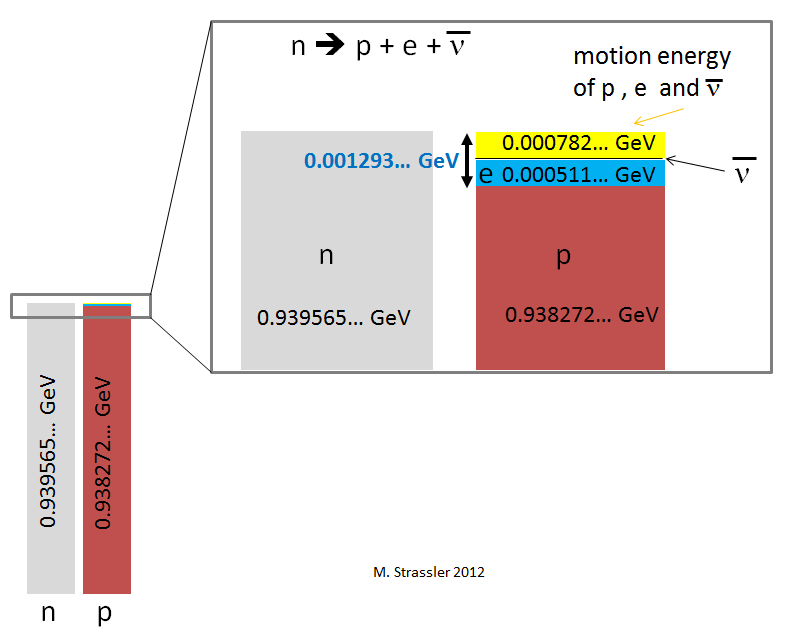Fig. 3La différence peut être compensée par l'énergie du mouvement. Elle est toujours positive. Il suffit de répartir le 0,000782 ... GeV supplémentaire entre les mouvements des particules pour que la dynamique du système soit préservée (croyez-moi, c'est possible). Ensuite, l'énergie sera économisée, car l'énergie de la masse du neutron s'est transformée en énergie de la masse et en énergie de mouvement du proton, de l'électron et du neutrino.
Je n'ai pas indiqué la quantité exacte d'énergie de mouvement qui a été expulsée par le proton, l'électron et le neutrino, car dans chacun des cas de désintégration des neutrons, l'énergie sera distribuée de différentes manières, juste de manière aléatoire (telle est la mécanique quantique). Seule l'énergie totale du mouvement sera toujours la même, 0,000782 ... GeV.
Deuteron est stable
Retour au deutéron. L'énergie totale d'un deutéron, comme celle d'un atome d'hydrogène, se compose de l'énergie positive de la masse de ses deux composants (proton et neutron), de l'énergie positive de mouvement des deux composants et de l'énergie d'interaction négative, plus que couvrant l'énergie du mouvement. De plus, comme pour toute particule ou système, la masse du deutéron sera égale à son énergie totale (plus précisément, l'énergie totale que vous mesurez quand il ne bouge pas par rapport à vous), divisée par c
2 , le carré de la vitesse de la lumière. En conséquence, si le deutéron se repose par rapport à vous, sur la base de sa masse mesurée égale à 1,875612 ... GeV / s
2 , nous pouvons dire que son énergie est
L'énergie de masse du deutéron = 1,875612 ... GeV =
• énergie massique proton + énergie massique neutronique,
• L'énergie du mouvement des protons + l'énergie du mouvement des neutrons,
• L'énergie d'interaction (négative et plus importante que l'énergie du mouvement).
<énergie massique des protons + énergie massique des neutrons
= 0,938272 ... GeV + 0,939565 ... GeV = 1,877837 ... GeV
Par conséquent, l'énergie de liaison du deutéron est
1,875612 ... GeV - 1,877837 ... GeV = -0,002225 ... GeV
Fig. 4L'énergie de liaison négative signifie, comme dans le cas d'un atome d'hydrogène, qu'un deutéron ne peut pas simplement s'effondrer dans un neutron et un proton, comme le montre la Fig. 4. Cela violerait la conservation de l'énergie, qui stipule qu'une particule en décomposition doit être plus massive que les particules dans lesquelles elle se désintègre. Comme le montre la fig. 5, vous ne pouvez en aucun cas économiser de l'énergie. Le neutron et le proton ont plus d'énergie de masse que le deutéron, et il n'y a pas de source d'énergie négative qui peut absorber le déficit énergétique, car il n'y a pas d'énergie d'interaction entre le proton éloigné et le neutron, et il n'y a pas d'énergie de mouvement négative. Cela signifie que le processus de la Fig. 4 ne peut pas arriver.
Fig. 5
Le neutron à l'intérieur du deutéron ne peut pas se désintégrer
Une étape est restée, et elle, par rapport aux précédentes, est assez simple. La question est: pourquoi un neutron ne peut-il pas se désintégrer à l'intérieur d'un deutéron?
Disons qu'il a éclaté: que reste-t-il? Ensuite, nous aurons deux protons, un électron et un antineutrino; voir la photo 6. Deux protons se repoussent - ils ont une charge électrique positive et une force électrique les repousse. Une forte interaction nucléaire, en essayant de les rapprocher, n'est pas aussi forte que celle d'un neutron avec un proton, et l'effet combiné des deux forces sera répulsif. En conséquence, cette interaction repoussera les protons. Pendant ce temps, l'électron et l'antineutrino quitteront également la scène.
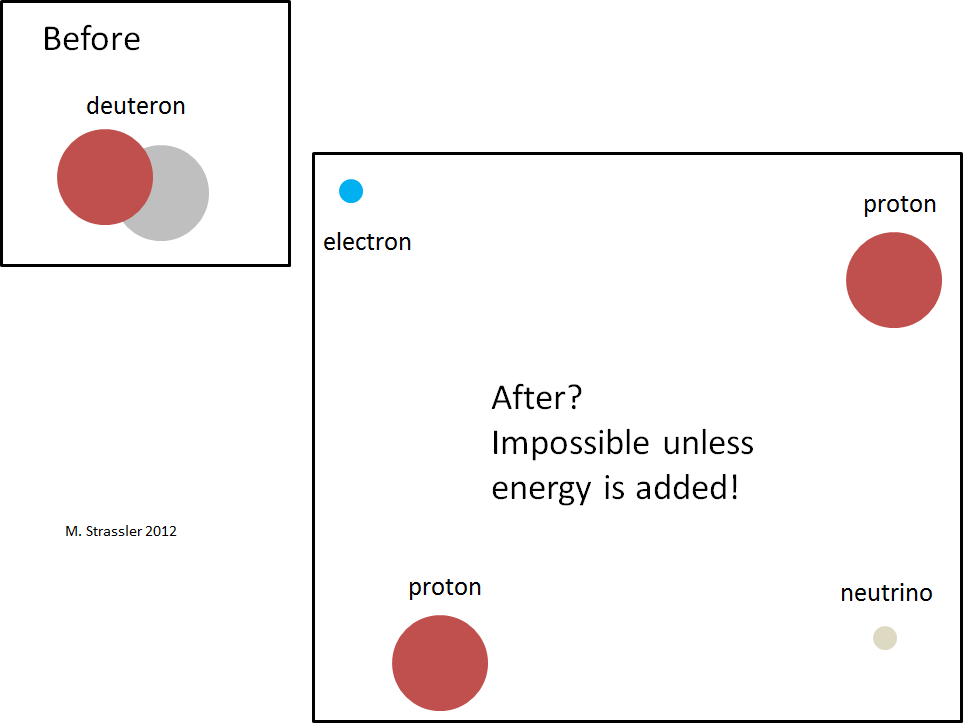Fig. 6Lorsque les quatre particules sont éloignées les unes des autres (comme le montre grossièrement la figure 6, mais imaginez qu'elles se dispersent encore plus), il n'y aura pas d'énergie d'interaction significative entre elles. L'énergie du système ne sera constituée que de la somme des énergies des masses de particules et des énergies de mouvement. Puisque l'énergie du mouvement est toujours positive, l'énergie minimale que les particules peuvent avoir sera égale à la somme de leurs énergies de masse. Mais cette énergie est supérieure à l'énergie de masse du deutéron (Fig. 7)! Même l'énergie de masse de deux protons, 1,876544 ... GeV est déjà supérieure à l'énergie de masse du deutéron. Et un 0,000511 GeV supplémentaire ne verse que du sel sur la plaie.
Par conséquent, le neutron à l'intérieur du deutéron ne peut pas se désintégrer; l'énergie d'interaction qui maintient le deutéron abaisse sa masse - suffisamment basse pour que la désintégration des neutrons à l'intérieur du deutéron viole la conservation de l'énergie!
Fig. 7Autres noyaux atomiques
Et il en va de même pour tous les noyaux stables de la nature. Mais ne pensez pas que chaque fois que vous combinez neutrons et protons, le résultat est un noyau stable! Les noyaux stables sont extrêmement rares.
Si vous prenez des protons Z et N neutrons et essayez d'en faire un noyau, alors pour la plupart des variantes Z et N, vous ne réussirez pas. La plupart de ces noyaux se désintégreront instantanément, ils ne se formeront pas du tout. En gros, la force d'attraction entre les protons Z et les neutrons N est plus forte lorsque Z est approximativement égal à N. Par contre, les protons sont repoussés les uns des autres en raison de l'interaction électromagnétique. Cette force augmente avec l'augmentation de Z. La concurrence de ces deux effets suggère que le noyau est susceptible d'être stable lorsque Z est légèrement inférieur à N; et plus Z et N sont grands, plus la différence entre Z et N. devrait être grande. Cela peut être vu sur la Fig. 8. Seuls les noyaux marqués en noir sont stables; ils sont situés dans ce qu'on appelle poétiquement la «vallée de la stabilité».
Et quels types de noyaux sont indiqués par la couleur? Il s'avère qu'il existe de nombreux noyaux qui se désintègrent encore, mais qui peuvent vivre pendant un certain temps. Souvent, nous appelons ces objets «instables» et ceux qui vivent assez longtemps sont «métastables». L'utilisation des mots dépend du contexte. Le neutron vit 15 minutes. Il y a des noyaux qui vivent pendant quelques millisecondes, jours, décennies, millénaires et même des milliards d'années. Nous appelons ces noyaux radioactifs; ce sont les conséquences dangereuses des cas impliquant des rayonnements ou des armes, et les outils utilisés dans les détecteurs de fumée et pour lutter contre le cancer, entre autres.
Il existe de nombreuses façons dont ces noyaux peuvent se désintégrer, mais certains d'entre eux se désintègrent, transformant un neutron en proton à l'intérieur du noyau. Nous le savons en augmentant la charge du noyau et par le fait qu'un électron en vole avec l'antineutrino. D'autres peuvent même se désintégrer, transformant un proton en neutron! Nous le savons parce que la charge du noyau diminue et qu'un positron (anti-électron) s'en échappe. La physique nucléaire très compliquée est impliquée dans le calcul de la quantité de vie d'un certain noyau et comment il va se désintégrer - ici je ne donnerai pas de cours à ce sujet (et je ne suis pas un expert).
Fig. 8Il suffit de dire que l'énergie négative de l'interaction des particules, combinée à la conservation de l'énergie, peut changer tout le jeu, rendant impossible certains processus qui sont possibles dans des conditions ordinaires - et vice versa.