Nous comprenons la physique des particules: 1) une balle sur un ressort, la version newtonienne

1. Balle sur ressort, version newtonienne
2. Une boule quantique sur un ressort
3. Vagues, look classique
4. Les vagues, l'équation classique du mouvement
5. Ondes quantiques
6. Champs
7. Les particules sont des quanta
8. Comment les particules interagissent avec les champs

Comprendre en termes généraux les bases de la physique des particules - et c'est notre compréhension actuelle de la plupart des phénomènes élémentaires de l'Univers - n'est pas si difficile. Ce sera plus facile pour vous si vous avez fréquenté une école de physique et de mathématiques ou terminé la première année de collège. Mais si vous traitez de l'algèbre, de la trigonométrie et (éventuellement, mais pas nécessairement) des bases de la différenciation et de l'intégration, vous pouvez alors comprendre comment les champs fonctionnent et comment les particules apparaissent. Vous n'avez besoin de me croire sur parole qu'une seule fois, concernant un aspect de la mécanique quantique. Dans ce cas, je ne donnerai pas de formules mathématiques, mais je vous montrerai simplement les réponses toutes faites. Mais après avoir accepté cet aspect, tout le reste sera clair.


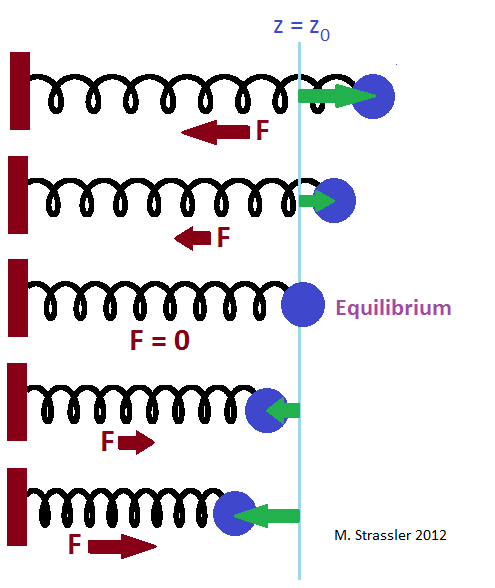Fig. 1

Pour comprendre la physique des particules, de la physique de l'école, vous devez vous rappeler une seule chose - comment fonctionne un ressort. En fait, tout ce qui rebondit, vibre, sonne, vibre, se balance d'avant en arrière, est un exemple de ressort.

Imaginez que nous ayons placé une balle à la fin d'un ressort. Les mouvements du ressort et les équations le décrivant sont simples. Pour commencer, nous rappelons les bases du comportement du ressort, puis nous étudions le comportement de la balle - oscillation. Et enfin, pour les esprits les plus curieux, nous considérerons les équations menant à ce type de mouvement.

Oscillateur harmonique (alias une balle sur un ressort)

La balle sur le ressort a une position d'équilibre; si vous y mettez la balle et la relâchez, le ressort ne la poussera dans aucune direction et la balle restera immobile. Ceci est la ligne bleue de la fig. 1. Si vous éloignez le ballon de la position d'équilibre (flèches vertes), le ressort ramènera le ballon avec la force F (flèches rouges). Plus vous tirez la balle loin, plus le ressort la retire fort (au moins jusqu'à ce que vous cassiez le ressort ou que vous le cassiez sous pression).

Mouvement oscillant (saut)

Nous appelons la direction de déplacement de la balle "direction z", et définissons l'axe z de sorte que z = z ₀ correspond à la position d'équilibre de la balle sur le ressort. Supposons que nous tirions la balle de cette position, la maintenions pour qu'elle ne bouge pas, à la position z = z ₀ + A; puis, à un certain moment t = 0, nous le libérons. La balle commencera à sauter ici et là - voir fig. 2. L'amplitude des sauts - l'amplitude des oscillations - est égale à A. Elle peut être arbitrairement grande ou petite; vous seul choisissez combien tirer la balle de la position d'équilibre. Mais vous ne contrôlez pas la fréquence des sauts - la fréquence des oscillations ν - se produit. Il se révèle être le même, quelle que soit la valeur de A. Il est déterminé uniquement par les propriétés de la balle et du ressort, et non par ce que vous faites.

À des fins scientifiques, il est extrêmement important de décrire les observations à l'aide d'une formule mathématique. La position de la boule z est fonction du temps t, écrit par nous comme z (t), qui prend la forme:

$$

$$z (t) = z_0 + A cos [2 \ pi \ nu t]$$

Où, comme d'habitude, cos est le cosinus, π est le nombre pi de la géométrie du cercle, z ₀ est la position d'équilibre de la balle, et A et ν (nu) sont l'amplitude et la fréquence des oscillations. La fonction cosinus est oscillatoire, donc cette formule décrit des mouvements oscillatoires d'amplitude A et de fréquence ν. Des exemples de mouvement oscillatoire d'une balle sur un ressort avec différentes valeurs de l'écart initial et de l'amplitude totale A sont montrés sur la Fig. 2, qui montre également que pour une boule donnée sur un ressort, la fréquence ν ne dépend pas de l'amplitude A.

Petits caractères: l'amplitude et la fréquence sont supérieures à zéro. Si A est négatif, alors l'amplitude sera –A. En fait, l'amplitude est en fait | A |, c'est-à-dire le module de magnitude.


Fig. 2

Ce qui est très important à retenir sur l'amplitude et la fréquence de la balle et du ressort (en physique pré-quantique classique):
• l'amplitude A peut être sélectionnée n'importe laquelle;
• la fréquence ν est déterminée par la bille et le ressort, et pour choisir une fréquence différente, vous devez remplacer le ressort ou la bille.

La période de chaque oscillation (combien de temps il faut au ballon pour avancer et reculer exactement une fois) sera appelée T, et cette période est simplement l'inverse de la fréquence: T = 1 / ν. Si la période est de 5 secondes, la fréquence est une fois toutes les cinq secondes, ou 1/5 seconde (ce qui est souvent appelé 1/5 Hertz ou Hz).

Une autre petite impression: dans tout système réel de ressort et de boule que vous rencontrerez dans la vie de tous les jours, la friction conduira au fait que A diminuera progressivement et atteindra finalement zéro lorsque le mouvement s'arrêtera. Les formules qui prennent en compte la friction lors du mouvement ne sont pas beaucoup plus compliquées, mais nous n'en aurons pas besoin. Par conséquent, je suppose toujours que le frottement est faible, A diminue très lentement et nous pouvons simplement utiliser des formules simplifiées qui ignorent le frottement. Mais il est important de savoir: le frottement réduit A, mais, à moins qu'il ne soit extrêmement fort, n'affecte pas ν et T! La fréquence d'oscillation reste la même malgré une diminution d'amplitude. Par conséquent, la note que la corde de guitare produit après l'avoir tirée ne change pas, même lorsque le son résultant s'estompe progressivement.

Encore une chose: il existe une belle formule pour l'énergie stockée dans un ressort oscillant. Il est proportionnel au carré de l'amplitude et au carré de la fréquence:

$$

$$E = 2 \ pi ^ 2 \ nu ^ 2 A ^ 2 M$$

C'est en partie l'énergie de mouvement de la balle (cinétique) et en partie l'énergie d'interaction (potentiel) stockée au printemps, et lorsque la balle oscille d'avant en arrière, les fractions de ces énergies dans l'énergie totale changent constamment. Mais l'énergie totale E reste constante.

Petits caractères: il y a encore l'énergie de la masse de la balle, Mc ² , mais on ne la suit pas, car elle est toujours là, le ressort bouge avec, ou pas.

La même formule d'oscillation s'applique à presque tout ce qui tremble ou saute seulement si ces sauts ne sont pas trop grands. Une boule roulant au fond du bol; une voiture sautant sur de mauvais amortisseurs; corde vibrante d'un violon ou d'une guitare; barre de xylophone après l'avoir frappé; etc.

L'équation du mouvement vibratoire (sauts mathématiques)

Rappelons maintenant les formules de base qui nous expliquent pourquoi la balle sur le ressort oscille.

Comme nous l'avons mentionné au début (Fig.1), la boule sur le ressort a une position d'équilibre, que nous avons appelée z = z ₀ . Supposons qu'à un moment donné (soit nous avons tiré le ballon, soit il a hésité), il se trouve dans une position différente, z. Si z> z ₀ , c'est-à-dire si le déplacement par rapport à la position d'équilibre z - z _{0 est} supérieur à zéro, alors le ressort créera une force dirigée dans la direction négative z pour ramener la balle au point d'équilibre. Inversement, si z <z ₀ , c'est-à-dire que le déplacement par rapport à l'équilibre z - z _{0 est} négatif, alors le ressort créera une force dirigée dans la direction positive z, là encore pour ramener la balle au point d'équilibre. Et plus la balle est éloignée de la position d'équilibre, plus le ressort tire fort. La force F créée par le ressort est liée au déplacement de la balle de l'équilibre par l'équation

$$

$$F = - K (z - z_0)$$

Où K est une valeur positive, en fonction d'un ressort spécifique, appelée constante du ressort.

Notez pourquoi cette formule est vraie:

• Si la balle est en position d'équilibre, F = 0. Le ressort ne crée pas de force, et si la balle n'a pas bougé en position d'équilibre, elle y restera.
• Si l'écart est supérieur à zéro, la force est négative.
• Si l'écart est négatif, la force est positive.
• Plus l'écart est grand, plus la force est grande.

Ensuite, nous passons à la deuxième loi du mouvement de Newton, qui stipule que sous l'influence de la force F, une boule de masse M se déplacera avec l'accélération a, où F = M a. Remplacez-le dans la formule et obtenez

$$

$$M a = - K (z - z_0)$$

ou

$$

$$a = - K / M (z - z_0)$$

C'est une équation presque nécessaire pour nous, à partir de laquelle nous pouvons dériver l'équation des oscillations. Il suffit de rappeler la relation entre a et z. Pour cela, il est important de rappeler la relation entre a et la vitesse v, et entre v et z. Ce ratio est l'un des deux changements au fil du temps:
• La vitesse est un changement de position dans le temps, v = dz / dt
• L'accélération est un changement de vitesse dans le temps, a = dv / dt

Ajouter et obtenir

$$

$$a = d (dz / dt) / dt = d ^ 2z / dt ^ 2$$

L'accélération est le changement dans le temps d'un changement de position dans le temps.

Nous pouvons réécrire notre équation d'équation de mouvement

$$

$$d ^ 2z / dt ^ 2 = - K / M (z - z_0) \ quad (*)$$

Où z est une notation courte pour z (t). Et maintenant, nous pouvons vérifier que le mouvement vibratoire z (t) = z ₀ + A cos [2 π ν t] sera une solution pour cette équation de mouvement. Nous devons d'abord calculer la vitesse d'une particule comme un changement de sa position dans le temps:

$$

$$d / dt (z_0 + A cos [2 \ pi \ nu t]) = - (2 \ pi \ nu) Un péché [2 \ pi \ nu t]$$

(dz ₀ / dt = 0, car la position d'équilibre z ₀ ne change pas avec le temps, et d / dt (cos wt) = -w sin wt); puis nous calculons l'accélération de la particule comme un changement de sa vitesse dans le temps:

$$

$$d / dt [- (2 \ pi \ nu t)] = - (2 \ pi \ nu) ^ 2 A cos [2 \ pi \ nu t]$$

(puisque d / dt (sin wt) = w cos wt). En conséquence

$$

$$d ^ 2z / dt ^ 2 = - (2 \ pi \ nu) ^ 2 A cos [2 \ pi \ nu t] = - (2 \ pi \ nu) ^ 2 (z - z_0)$$

Dans la dernière étape, j'ai utilisé la formule z (t) = z ₀ + A cos [2 π ν t] pour le mouvement oscillatoire. L'équation finale est la même que notre équation de mouvement [ $$$d ^ 2z / dt ^ 2 = - K / M (z - z_0)$ ], étant donné que (2 π ν) ² = K / M, si la fréquence d'oscillation est

$$

$$ν = \ frac {\ sqrt {K / M}} {2 \ pi}$$

Et nous, en fait, avons constaté que notre équation de mouvement implique que le ressort oscillera avec la fréquence indiquée, que cette fréquence ne dépend pas de A - elle dépend uniquement des propriétés du ressort (K) et de la boule (M) - et que indépendamment de la quantité A pour l'équation, il existe une solution. Par conséquent, nous pouvons choisir n'importe quel A, selon la distance à laquelle nous tirons la balle de la position d'équilibre avant de la relâcher.

Résonance

La résonance est l'un des phénomènes naturels les plus importants, à la fois dans la vie ordinaire, où elle joue un rôle dans de nombreux aspects de la technologie et de la musique, et dans les processus de base du monde physique, en particulier en physique des particules.

Tout d'abord, rappelez-vous comment fonctionne le swing. Un swing, comme une balle sur un ressort ou tout autre pendule, est un oscillateur - il oscille d'avant en arrière avec une certaine fréquence, qui ne dépend pas de l'amplitude du swing. Dans le cas d'un swing, cette affirmation reste vraie jusqu'à ce que l'amplitude soit très grande. Vous savez probablement par expérience que pour balancer un enfant plus haut, vous devez pousser la balançoire vers l'avant une fois par cycle afin que l'amplitude du balancement augmente constamment. Si vous poussez la balançoire vers l'avant plusieurs fois par cycle, ou une fois tous les deux cycles et demi, vous augmenterez parfois l'amplitude de la balançoire, et parfois la réduirez. Évidemment, il y a quelque chose de spécial à aligner la fréquence à laquelle vous poussez la balançoire avec la fréquence naturelle de la balançoire elle-même.

De même, si l'enfant lui-même sait balancer la balançoire, il sait qu'il doit balancer ses jambes en même temps que la fréquence naturelle de la balançoire afin d'augmenter l'amplitude de la balançoire. Swing d'une manière différente, et l'amplitude ne augmentera pas.



Vous pouvez voir comment cela se produit avec le ballon au printemps. Regardez l'image. Sur la gauche, une balle oscille d'avant en arrière autour d'une position d'équilibre. Il hésite, sans chocs extérieurs. Il oscille avec la fréquence naturelle du ressort ν. La fréquence est √ K / M, où K est la force du ressort, M est la masse de la balle.

A droite sur la fig. vous pouvez voir ce qui arrive à une autre boule, noire, de masse égale à la première, sur le même ressort, qui est poussée avec la force F (son amplitude et sa direction sont indiquées par la flèche rouge), qui oscille avec une fréquence ν _F différente de ν. Une balle noire se comporte comme une balançoire qui pousse trop rarement; ils se déplaceront de façon complexe et ne monteront pas haut. Dans la fig. on voit que la balle n'oscille pas très doucement, et l'amplitude des oscillations est faible. Vous pouvez voir comment il "essaie" d'osciller avec une fréquence naturelle, bien que son mouvement général soit répété avec une fréquence ν _F.

Ensuite, la figure montre le cas dans lequel la force oscille avec une fréquence ν _F , qui est beaucoup plus élevée que la fréquence ν. Encore une fois, vous pouvez voir comment il "essaie" d'osciller avec une fréquence naturelle, mais il ne réussit pas à le faire avec une grande amplitude, car une force oscillant rapidement peut soit la pousser dans ou contre le mouvement, augmenter ou diminuer l'amplitude .

Et à la fin, le cas est montré lorsque la force oscille avec la fréquence naturelle du ressort, ν _F = ν. La balle réagit très différemment: l'amplitude des oscillations ne cesse de croître, et la boule noire oscille aussi facilement et en douceur que la boule blanche à gauche, mais avec une augmentation d'amplitude. C'est une résonance.

En conséquence: si ν _F diffère de ν - si la force ne permet pas à la balle d'entrer dans la résonance - elle se déplacera, mais à contrecœur, et son mouvement sera très différent du naturel, d'une simple oscillation de fréquence ν. Au contraire, si la fréquence de la force correspond à la fréquence naturelle - si la force introduit la balle en résonance - alors la force pousse la balle beaucoup plus efficacement et le mouvement qui en résulte est plus impressionnant. Nous le savons intuitivement; en poussant la balançoire avec une fréquence naturelle, l'enfant (ou le parent) balance la balançoire de plus en plus haut.

L'un des aspects importants de la résonance en physique des particules est le fait que, dans certaines circonstances, des particules peuvent être générées en raison d'un mécanisme très similaire: après une collision de deux particules, une force est obtenue avec exactement la même fréquence que nécessaire pour en créer une troisième.

La prochaine fois: boule quantique sur un ressort

C'est le comportement d'une balle sur un ressort en physique classique, pré-quantique. La mécanique quantique change de nombreux concepts , mais la chose la plus importante est la suivante: nous pouvons toujours choisir A, mais A ne peut pas être de n'importe quelle taille. Il ne peut prendre que certaines valeurs proportionnelles à la racine carrée des entiers.