Nous comprenons la physique des particules: 3) ondes, forme classique

1. Balle sur ressort, version newtonienne
2. Une boule quantique sur un ressort
3. Vagues, look classique
4. Les vagues, l'équation classique du mouvement
5. Ondes quantiques
6. Champs
7. Les particules sont des quanta
8. Comment les particules interagissent avec les champs

Après avoir traité les équations des oscillations - décrivant presque tout ce qui saute, vibre, roule d'avant en arrière, comme une balle sur un ressort - nous pouvons passer au phénomène naturel tout aussi commun, les vagues. Les vagues sont partout: son et lumière, tremblements de terre, ondulations à la surface de l'étang, etc.


Fig. 1

Mais avant cela, je vous préviens que le terme «onde» peut être trompeur, car en physique il ne signifie pas la même chose qu'en anglais. En physique, cela ne signifie pas ce que nous appellerions habituellement une vague au bord de l'océan - une crête et un creux. En physique, les vagues sont une séquence d'ondes, plusieurs crêtes et creux qui se déplacent ensemble dans la même direction. Dans une vague de la forme la plus simple, toutes les arêtes sont de la même hauteur et sont espacées d'une distance les unes des autres. Nous considérerons un tel cas.

Les vagues sont un phénomène exceptionnel, si vous y réfléchissez. Imaginez que vous et votre ami avez pris une longue corde et que vous l'avez tirée fermement dans la pièce (Fig. 2). Imaginez ensuite que votre ami a bavardé plusieurs fois de haut en bas avec une extrémité de la corde (verte). Une vague apparaîtra à son extrémité de la corde et elle traversera la pièce jusqu'à votre extrémité de la corde (rouge).


Fig. 2

C'est incroyable. Je veux dire - c'est vraiment incroyable, fort et critique pour tout dans notre univers, y compris vous personnellement. Regardez ce qui s'est passé. Aucun des objets physiques ne s'est déplacé de gauche à droite - avant que votre ami ne commence à bouger le bout de la corde, il a été étiré à travers la pièce, et à la fin, après que votre bout de corde cesse de vibrer et que la vague disparaisse, la corde restera tendue à travers l'ensemble chambre, comme c'était. Et pourtant! L'énergie et l'information se déplaçaient dans la pièce. La vague en chemin transporte l'énergie dépensée par votre ami sur les vibrations de la corde - et transmet sous sa forme des informations sur le nombre de fois et la vitesse à laquelle il l'a tirée - vers vous, où elle fait trembler votre main. Et dans ce cas, elle vous serrera même la main autant de fois et dans cette séquence. Ouah! Aucun objet physique ne se déplaçait dans la pièce, et l'énergie et l'information se déplaçaient.

Ou attendez. Mais ne faut-il pas considérer la vague comme un objet physique? Aussi physique que la corde elle-même?

En nous souvenant de cette question la plus profonde, passons à un petit nombre de formules mathématiques nécessaires pour décrire l'apparence et le comportement de l'onde, puis utilisons un peu plus de mathématiques pour écrire les équations dont les solutions sont les ondes. C'est similaire à ce que nous avons fait pour une boule à ressort classique.

Formule pour une onde infinie à un certain moment

Cette série d'articles immédiatement après la balle sur le ressort va aux vagues car la vague est une sorte de double oscillateur. Il fluctue à la fois dans le temps et dans l'espace. Nous désignerons le temps avec la lettre «t» et l'espace avec «x».

Faites attention à la fig. 3. Il représente une vague s'étendant dans les deux directions sur une grande distance, à laquelle de nombreuses crêtes et dépressions s'adaptent. Ceci est différent de la vague de la fig. 2, qui ne comporte que quelques crêtes et dépressions. Mais cette différence n'est pas pertinente - sur la Fig. 2 J'avais besoin d'illustrer ce que la forme d'onde exacte n'avait pas d'importance; Maintenant, nous allons nous concentrer sur la formule mathématique des vagues, et c'est beaucoup plus facile à faire si la vague a un grand nombre de crêtes et de dépressions de la même taille. De plus, ce cas se révélera très utile pour comprendre comment la mécanique quantique affecte le comportement des ondes.



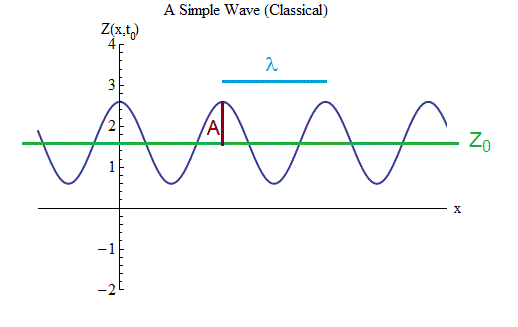
Fig. 3

Tout d'abord, nous devons déterminer la notation et noter une formule décrivant le mouvement et la forme d'onde de la Fig. 3, comme nous l'avons fait pour le ballon au printemps.

Le graphique montre la magnitude de l'onde Z en fonction de l'espace dans une certaine période de temps t = t ₀ - nous l'enregistrons comme Z (x, t ₀ ). En suivant l'onde dans l'espace, nous voyons qu'elle oscille vers l'avant et vers l'arrière, et Z augmente et diminue périodiquement. À tout moment, l'onde oscille dans l'espace.

Notez que Z n'a pas à être lié à la distance physique. Il peut s'agir de la hauteur de la corde, comme sur la fig. 2, ou cela peut être quelque chose de complètement différent, par exemple, la température de l'air à un certain point dans l'espace et le temps ou l'orientation d'un atome magnétique à un certain endroit d'un aimant. Mais x représente toujours la distance physique, et t est le temps.

Le plan de cette vague, Z (x, t ₀ ), a trois propriétés intéressantes, dont deux s'appliquent également à une balle sur un ressort.

1. Il existe une valeur d'équilibre Z ₀ située entre la plus grande valeur Z sur la crête et la plus petite valeur Z dans la dépression. La plupart du temps, nous étudions des vagues pour lesquelles Z ₀ = 0, car souvent la valeur Z ₀ n'a pas d'importance - mais pas toujours.
2. L'onde a une amplitude A, une valeur par laquelle Z passe de la valeur d'équilibre au sommet de chaque crête ou de la même valeur au bas de chaque dépression.
3. La vague a une longueur - la distance λ entre les crêtes adjacentes, ou, ce qui est la même, entre les creux voisins, ou, qui est la même, deux fois la distance entre la crête adjacente et le creux. Il décrit les oscillations dans l'espace de la même manière qu'une période (égale à 1 / fréquence) décrit l'oscillation dans le temps d'une balle sur un ressort.


Fig. 4

Ce qui nous rappelle le formulaire de la Fig. 3? Il ressemble à un graphique de la fonction sinus ou cosinus - voir fig. 4, où cos (w) est tracé sur w. Cos (w) est une fonction oscillante, qui a une position d'équilibre évidente à zéro, son amplitude est 1 et la longueur d'onde est 2π. Comment passer de la fig. 4 à la formule de l'onde de la Fig. 3? Tout d'abord, nous multiplions cos (w) par A, de sorte que l'amplitude est égale à A. Ensuite, nous ajoutons Z ₀ à la formule entière pour la déplacer vers la valeur d'équilibre souhaitée (si A = 0, il n'y a pas d'oscillation, et tout repose au point Z = Z ₀ ). Et enfin, remplacez w par 2πx / λ, puisque cos (w) a des arêtes à w = 0 et w = 2 π, donc, à cos (2πx / λ), les arêtes seront à x = 0 et x = λ. Tous ensemble, cela nous donne

$$

$$Z (x, t_0) = Z_0 + A cos (2 \ pi x / \ lambda)$$

Il s'agit presque de la même formule qui décrit le mouvement d'une balle sur un ressort dans le temps:

$$

$$z (t) = z_0 + A cos (2 \ pi \ nu t) = z_0 + A cos (2 \ pi t / T)$$

Où ν est la fréquence d'oscillation et T = 1 / ν est la période d'oscillation. Voir l'analogie: une période se réfère au temps comme une longueur d'onde se réfère à l'espace.

Encore une note avant de continuer. Je pourrais aussi écrire:

$$

$$Z (x, t_0) = Z_0 + A cos (- 2 \ pi x / \ lambda)$$

Puisque cos [w] = cos [-w]. Le fait que nous pouvons facilement remplacer le moins dans la formule de la forme d'onde sera important plus tard.

Formule pour une vague sans fin dans un endroit spécifique

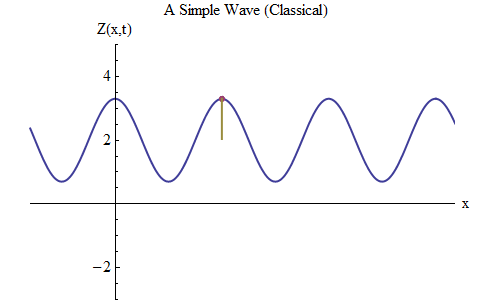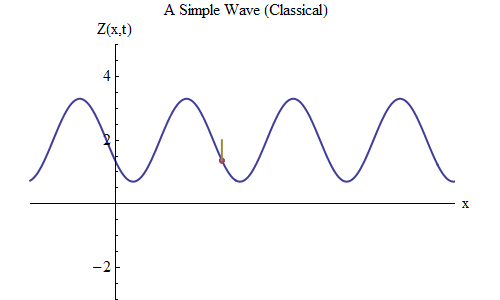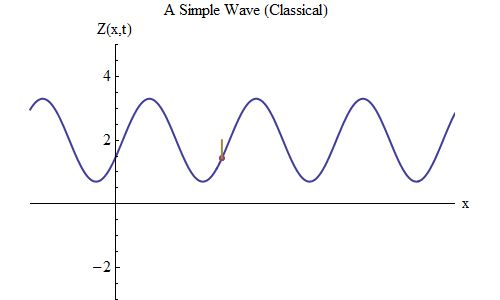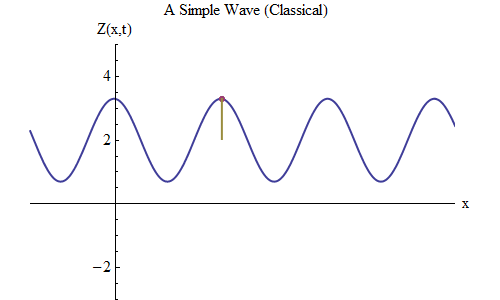Fig. 5

Maintenant, posons une autre question: voyons comment la vague change dans le temps, suivant un certain point sur la corde, et voyons comment elle se comporte et se déplace. Ceci est illustré sur la fig. 5: là j'ai désigné un point spécifique x ₀ , qui au temps t ₀ est sur la crête. L'onde se déplace vers la droite et suit la taille de l'onde Z au point x ₀ , changeant dans le temps: Z (x ₀ , t). Et vous verrez immédiatement que la hauteur des vagues à un certain point se comporte exactement comme une balle sur un ressort! Par conséquent, il aura exactement la même formule qu'une boule sur un ressort, en fonction de la fréquence ν, ou de la période T = 1 / ν, où T est le temps entre le moment où l'onde à x ₀ est sur la crête et le moment où elle s'approche à nouveau de la crête la prochaine fois.

$$

$$Z (x_0, t) = Z_0 + A cos (2 \ pi \ nu t) = Z_0 + A cos (2 \ pi t / T)$$

Formule complète de vagues infinies

Maintenant, nous avons besoin d'une formule pour Z (x, t) qui décrit l'onde représentée sur la Fig. 3 et 5 (ou similaire) aux points x à tout moment t. La bonne réponse est:

$$

$$Z (x, t) = Z_0 + A cos (2 \ pi [\ nu t - x / \ lambda]) = Z_0 + A cos (2 \ pi [t / T - x / \ lambda])$$

Il comprend les deux formules, pour un point fixe dans le temps et pour un point fixe dans l'espace.

Notez le signe moins devant x. J'ai mentionné que dans la formule pour Z (x, t ₀ ), vous pouvez remplacer un moins à volonté. Avec un moins devant x et un plus devant t, la formule décrit une onde se déplaçant vers la droite, comme dans les animations. Pour vérifier cela, notez que lorsque t / T - x / λ = 0, l'onde sera une crête car cos [0] = 1. Lorsque t = 0, au point x = 0 la crête. Mais si nous avançons un peu t, disons T / 10, alors la crête sera au point x = λ / 10, à droite de l'endroit où elle était à t = 0 - donc la crête (et toute la vague) se déplace vers la droite.

Qu'est-ce qui changera si vous placez un plus au lieu d'un moins dans la formule pour Z (x, t)? Ensuite, la crête sera à t / T + x / λ = 0, et dans ce cas, à t = T / 10, la crête sera à x = -λ / 10, à gauche de l'endroit où elle était à t = 0 - ce qui signifie , maintenant l'onde se déplace vers la gauche (Fig. 6).


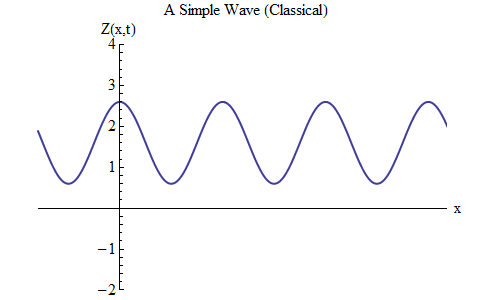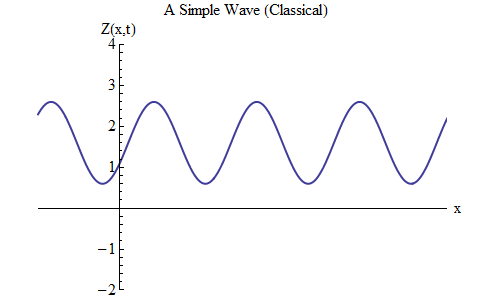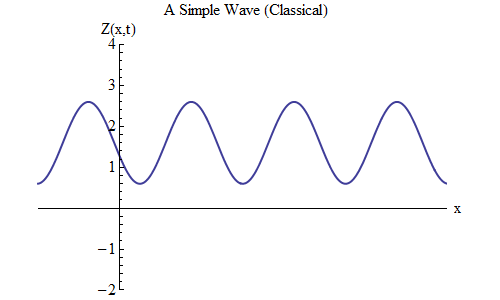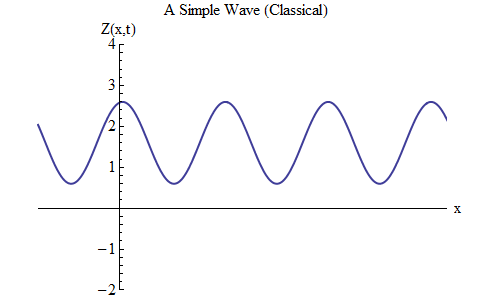Fig. 6

Les ondes, qui sont des fonctions de x et de t, peuvent se déplacer dans n'importe quelle direction, il nous suffit donc de choisir la bonne formule pour l'onde donnée. De manière générale, lorsque nous travaillons avec des vagues qui peuvent se déplacer non seulement le long d'une dimension spatiale x, mais le long des trois coordonnées x, y et z, ces vagues peuvent se déplacer dans n'importe quelle direction, et nous devrons choisir la bonne formule en fonction de la direction mouvement des vagues.

Petits caractères: on peut mettre un signe moins devant t, et pas avant x. Mais + t, + x est identique à –t, -x, car cela équivaudra à multiplier la formule entière à l'intérieur du cosinus par -1, et cos [w] = cos [-w]. Par conséquent, + t, + x et -t, -x donnent une onde se déplaçant vers la gauche, et + t, -x et -t, + x donnent une onde se déplaçant vers la droite.

Équation d'onde

Maintenant, comme dans le cas d'une balle sur un ressort, lorsque nous avons d'abord trouvé une formule pour le mouvement oscillatoire de la balle, puis regardé l'équation du mouvement, pour laquelle cette formule était une solution, nous ferons la même chose ici. Nous avons trouvé une formule pour la forme et le mouvement de la vague. Quelle équation de mouvement parmi les solutions a une telle formule? Nous apprenons dans le prochain article.