Nous comprenons la physique des particules: 6) les champs

1. Balle sur ressort, version newtonienne
2. Une boule quantique sur un ressort
3. Vagues, look classique
4. Les vagues, l'équation classique du mouvement
5. Ondes quantiques
6. Champs
7. Les particules sont des quanta
8. Comment les particules interagissent avec les champs

En fait, nous sommes allés sur le terrain il y a quelque temps, je ne vous avais tout simplement pas prévenu - je voulais me concentrer sur les vagues qui se produisent dans ces champs. Décrivant le comportement des ondes, nous avons exprimé leur forme et leur dépendance au temps en utilisant la fonction Z (x, t). Eh bien, Z (x, t) est un champ. C'est une fonction de l'espace et du temps avec une équation de mouvement qui détermine son comportement. Une fonction de mouvement appropriée serait telle que si Z augmente ou diminue à un certain point, alors Z diminuera ou augmentera aux points voisins un peu plus tard. Cette caractéristique permet aux vagues d'être parmi les solutions de l'équation.

Dans cet article, nous examinerons quelques exemples de champs Z (x, t) dont les équations de mouvement permettent aux ondes d'exister. L'interprétation physique de ces champs sera très différente. Ils décrivent les différentes propriétés de différents matériaux. Mais les équations qu'ils satisfont, et les vagues qu'ils démontrent, satisferont des mathématiques très similaires, et ils se comporteront de manière similaire, malgré leurs origines physiques différentes. Ce sera un point très important à l'avenir.

Et puis nous faisons quelque chose de radical - considérons les champs dans le contexte de la théorie spéciale de la relativité. Comme l'a montré Einstein, si vous corrigez l'espace et le temps et les forcez à ne pas conduire comme la plupart des gens l'attendent, vous obtiendrez un nouveau type de champ - de telle sorte que son interprétation physique n'est pas la propriété d'autre chose, mais un objet physique indépendant.

Champs ordinaires décrivant des choses ordinaires

Le champ Z (x, t) peut représenter de nombreuses grandeurs physiques différentes. Par exemple:
• La hauteur de la corde tendue à travers la pièce.
• La hauteur de l'eau dans la rivière.
• La densité du cristal ou du gaz.
• La position des atomes dans un aimant.
• Vitesse du vent.
• Température, densité ou pression atmosphérique.

Dans tous ces cas, il existe un champ Z (x, t): un champ de hauteur, un champ de densité, un champ d'orientation, un champ de vent et un champ de température. Sa valeur sous la forme d'une fonction de l'espace et du temps nous indique la hauteur, la densité, l'orientation, la vitesse du vent ou la température d'un milieu - une corde, une rivière, un cristal, un gaz, un aimant, de l'air - en tout lieu à tout moment. Son équation de mouvement montre comment Z (x, t) peut se comporter en principe. Il montre également comment prédire le comportement de Z (x, t) dans le futur, si nous connaissons exactement son comportement dans le présent et le passé.

Dans chaque exemple, il y a un champ et un environnement, et nous ne devons pas confondre le champ avec l'environnement. Le champ décrit et caractérise simplement l'une des nombreuses propriétés de l'environnement correspondant. Des environnements absolument différents peuvent avoir des champs de comportement très similaires avec des ondes très similaires - nous le verrons toujours.

Encore une fois, je clarifierai un point qui provoque souvent des malentendus. En général, un champ peut n'avoir rien à voir avec la distance physique dans l'espace. Oui, dans les articles 3 et 4, j'ai utilisé l'exemple d'un bœuf sur une corde pour illustrer ce que peut être Z (x, t), car il est beau et intuitif. J'ai aussi souvent tracé des graphiques Z (x, t) pour les vagues. Cela peut vous donner la fausse impression que Z (x, t) est toujours associé à des vagues qui font qu'un objet physique (comme une corde) se déplace d'une distance Z dans une direction perpendiculaire à l'axe x. Mais ce n'est pas le cas, comme nous le montreront trois de nos quatre exemples.

Champ de hauteur de corde

Tout d'abord, considérons notre premier exemple d'ondes, une corde oscillante. Dans ce cas, le rôle de Z (x, t) est le champ de hauteur, que nous appelons H (x, t). Il nous indique la hauteur de la corde en chaque point de l'espace sur l'axe x qui longe la corde à tout instant t. Si la corde est à la hauteur d'équilibre H ₀ , alors H (x, t) = H ₀ . Le champ de hauteur est une constante dans l'espace et le temps. Si une simple vague la traverse, le champ de hauteur sera décrit par notre célèbre formule de vague des articles précédents.

Si nous connaissons H (x, t), nous connaissons la hauteur de la corde en tout point de l'espace et du temps. Si nous savons ce que fait la corde maintenant et ce qu'elle a fait récemment, en utilisant l'équation du mouvement, nous pouvons prédire ce qu'elle fera à l'avenir. Cela nous en dit peu sur la corde elle-même. Le champ de hauteur ne nous donne que ce que son nom l'indique: la hauteur de la corde. Une corde est un milieu physique dont la hauteur est représentée par un champ H (x, t); il ne nous dit rien sur la couleur de la corde, son épaisseur, sa tension, sa matière, etc.

Dans la fig. 1 J'ai fait pour vous une animation d'une onde dans un champ de hauteur allant de gauche à droite. Il peut sembler que j'ai peint la même chose deux fois, d'abord en vert puis en orange. Mais ce n'est pas la même chose. La courbe orange est la corde elle-même, se déplaçant dans l'espace physique. Une courbe verte est un graphique représentant ce qui se passe avec H (x, t), indépendamment de ce que signifie H (x, t) (c.-à-d. La hauteur) ou de quel type d'environnement il s'agit. Et seulement dans ce cas, le graphique vert ressemble exactement à ce qui se passe dans le monde physique. Mais dans tous les autres cas, il n'en sera pas ainsi.


Fig. 1

Champ de déplacement du réseau

Supposons que nous ayons un milieu composé d'un cristal avec des atomes uniformément répartis à égale distance les uns des autres. Je les ai dessinés en photo. 2 en une dimension - vous pouvez imaginer des situations similaires en trois dimensions, mais pour l'instant, ce serait une complication inutile. J'ai également marqué chaque 10e atome en rouge pour vous permettre de suivre plus facilement leurs mouvements. Et j'ai aussi considérablement exagéré la distance entre les atomes - imaginez qu'entre deux points rouges, il y a plusieurs millions d'atomes, pas 10.

Nous regardons le champ de déplacement D (x, t), qui nous indique combien au moment t l'atome, généralement situé au point d'équilibre x, s'est déplacé de ce point dans le réseau. Cela signifie que dans le cas d'un état statique à partir duquel l'animation démarre, le champ est partout nul, D (x, t) = 0, car tous les atomes sont dans leur position habituelle. Ensuite, dans l'animation, les atomes individuels commencent à osciller d'avant en arrière, et leur mouvement, dans l'ensemble, se propage sous la forme d'une onde allant de gauche à droite. En haut de la figure, le graphique du champ de déplacement du réseau D (x, t) montre comment le champ se comporte lors du passage de l'onde. Notez que les champs de la Fig. 1 et 2 se comportent de manière similaire, bien que l'interprétation physique des champs soit très différente.


Fig. 2

Champ d'orientation magnétique

Qu'est-ce qu'un aimant permanent? Il se compose d'un ensemble d'atomes, dont chacun sert de petit aimant avec un champ magnétique minuscule, et ils sont tous alignés de sorte qu'ensemble, ils créent un grand champ magnétique. L'aimant est représenté sur la fig. 3, et en lui chaque atome est dirigé vers le haut. Dans ce cas, le champ d'orientation Θ (x, t) nous indique à quelle distance au temps t l'atome au point x s'est écarté de la verticale. Θ, en bref, sera l'angle entre l'aimant de chaque atome et la verticale. L'animation de la fig. 3 montre une onde dans un aimant dans laquelle les directions des aimants atomiques oscillent à gauche et à droite. Un graphique Θ (x, t) est affiché au-dessus de l'aimant vert; et encore, il a exactement la même apparence que dans les cas précédents.

Champ de pression d'air

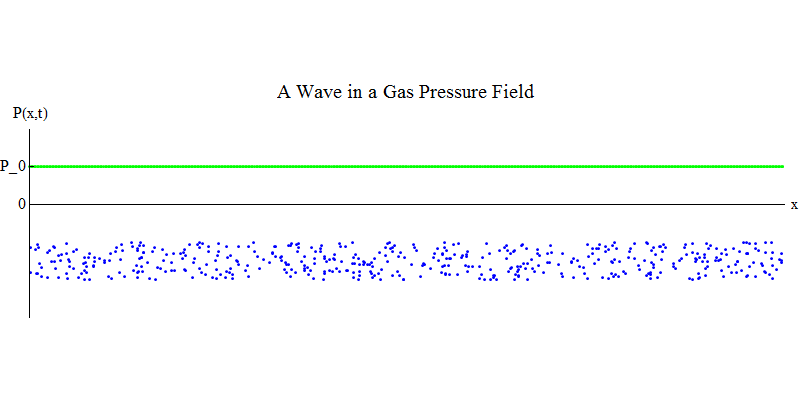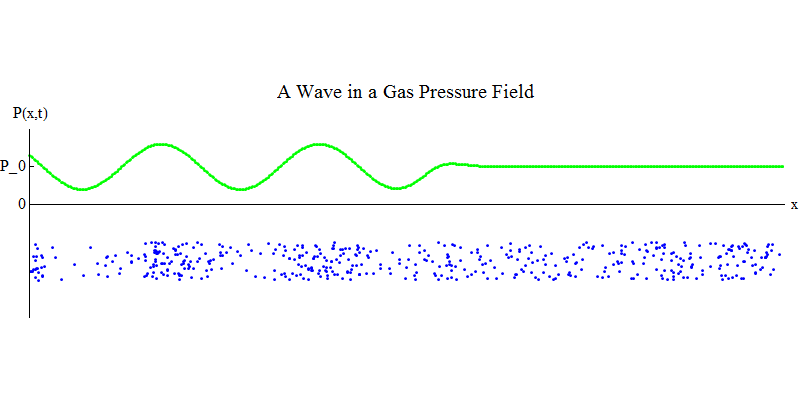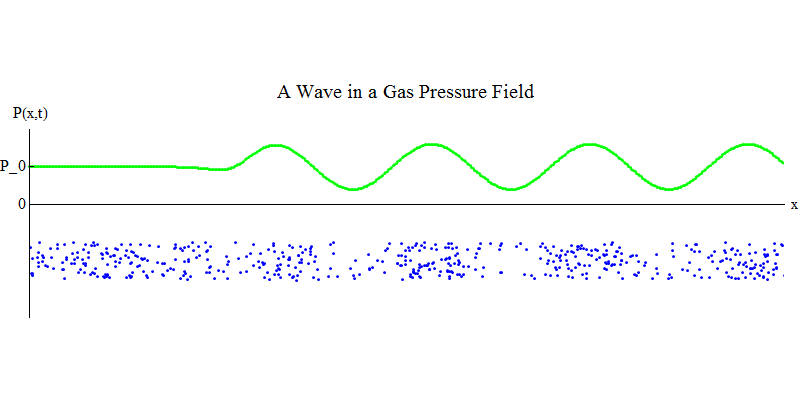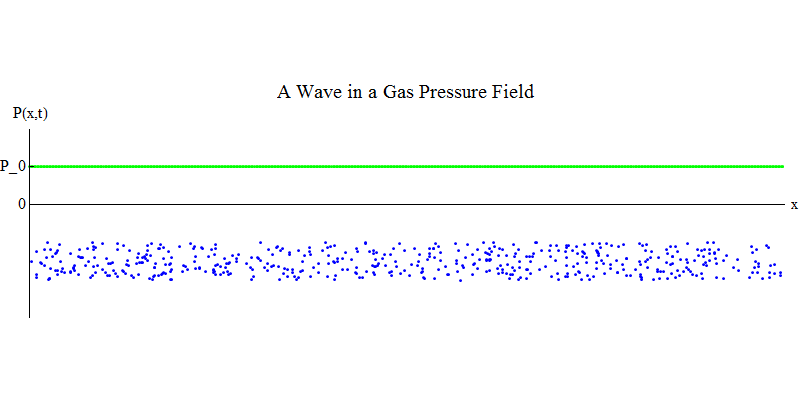
Considérons un gaz moléculaire dans un long tuyau. Le long du tuyau sera la dimension x. Les molécules de gaz se déplaceront presque aléatoirement, entrant en collision avec les parois du tuyau et entre elles. En équilibre, la densité (le nombre de molécules dans un volume donné) et la pression P (x, t) (la force agissant sur la surface d'une petite boule qui apparaît au point x au temps t) sont constantes. Mais les ondes sonores traversant le gaz feront osciller la pression et la densité, comme le montre la fig. 4. La densité et la pression augmentent et diminuent périodiquement. Les molécules avancent et reculent, bien qu'en moyenne elles ne bougent pas du tout, mais en même temps l'onde et son énergie se déplacent de gauche à droite à travers le gaz. Le graphique P (x, t) ressemble à nouveau de manière très similaire aux précédents.

Leçons importantes

Que pouvons-nous apprendre de quatre exemples montrant des vagues de classe 0? (L'équation du mouvement a une quantité, cw, et toutes les ondes dans le champ correspondant se déplacent avec la vitesse cw. Différents champs de classe 0 auront différentes valeurs de cw). Nous pouvons découvrir que le même comportement de champ peut émerger de champs physiquement différents existant dans des environnements physiquement différents. Malgré leur origine différente, les ondes dans le champ d'altitude, dans le champ de déplacement de réseau, dans le champ d'orientation magnétique et dans le champ de pression de gaz semblent identiques du point de vue des champs. Ils satisfont le même type d'équation de mouvement et la même relation numérique de fréquence et de longueur d'onde.

Petits caractères: à proprement parler, si vous créez des vagues d'une longueur suffisamment courte, vous pouvez toujours distinguer le comportement de différents supports. Dès que les longueurs d'onde sont égales à la distance entre les atomes de la corde, ou du cristal, ou de l'aimant, les équations d'onde que les ondes satisferont seront plus complexes que celles écrites par nous, et leurs détails distingueront les médias les uns des autres. Mais souvent, dans les expériences pratiques, nous ne sommes même pas près d'observer de tels effets.

Il en résulte que l'étude des ondes et de leurs quanta liés aux champs ne vous dira pas nécessairement ce qui sert de milieu, ou quelle est l'interprétation physique du champ - quelle est la propriété du milieu. Et même si vous savez d'une manière ou d'une autre qu'il s'agit d'un champ d'un certain type - par exemple, un champ de pression - vous ne pourrez généralement toujours pas dire de son comportement quelle pression il représente. Tout ce que vous pouvez apprendre en étudiant les vagues est de savoir si le champ appartient à la classe 0 ou à la classe 1, et quelle est la valeur de cw; ou découvrez que le champ appartient à une autre classe.

Dans certains cas, c'est très mauvais; le champ ne transmet que des informations partielles sur l'environnement. C'est parfois assez pratique; le champ est une chose plus abstraite et universelle que le matériel physique qu'il décrit.

Par conséquent, le champ ne définit pas l'environnement et son comportement ne dépend souvent pas des détails et des propriétés de l'environnement. À cause de ce que la question se pose.

Un champ physique pourrait-il exister - avec des ondes constituées de quanta se déplaçant dans l'espace et transférant de l'énergie - sans aucun support le supportant?

Champ sans milieu?

Vous ne pouvez pas entendre une chanson sans chanteur. Mais la chanson a une sorte d'existence indépendante; ça sonne différemment, selon qui la chante, mais en même temps il y a quelque chose d'inhérent à la chanson, une certaine qualité abstraite, grâce à laquelle elle peut toujours être reconnue. Cette entité abstraite est la mélodie de la chanson. On peut discuter, étudier, apprendre une mélodie, l'enregistrer avec un enregistrement musical, sans même l'entendre interprété par le chanteur. Beaucoup d'entre nous peuvent même nous le fredonner dans la tête. D'une certaine manière, une mélodie existe même si personne ne joue une chanson.

Si dans tous les exemples donnés par moi et dans tous les exemples que je peux donner, et qui vous seront intuitivement clairs, le champ décrit la propriété parmi, alors comment un champ peut-il exister sans environnement? Mais d'une manière ou d'une autre, les champs sont indépendants de leur environnement, car de nombreux champs différents peuvent se comporter de la même manière, malgré le fait qu'ils décrivent de nombreuses propriétés différentes d'environnements complètement différents. Il est donc probablement possible d'abstraire le champ de l'environnement.

En fait, ce n'est pas seulement possible, cela semble nécessaire. À tout le moins, il faut soit ne pas avoir de support, soit avoir un environnement qui ne peut pas être créé à partir de matière ordinaire, qui est fondamentalement différent de tous les médias que nous considérons, en ce sens qu'il fonctionne de telle manière (selon toutes les expériences) qu'il n'existe pas .

L'un des nombreux éléments radicaux de la théorie spéciale de la relativité d'Einstein de 1905 était l'idée que pour les ondes lumineuses - pendant des décennies considérées comme des ondes dans les champs électriques et magnétiques (ondes électromagnétiques), et se déplaçant à la même vitesse dans l'espace vide - il n'y a pas de milieu. Il n'y a que des champs.

Le milieu hypothétique était appelé "éther"; Einstein a fait valoir qu'une telle chose n'existe pas et a noté un ensemble d'équations pour lesquelles il n'était pas nécessaire. Je note qu'il y a encore un débat (souvent plus philosophique que physique) sur la nécessité ou non d'imaginer l'existence d'un environnement étrange très différent de la matière ordinaire. À ce jour, aucune preuve n'exige sa disponibilité.

Les éléments clés de la version d'Einstein de la relativité (contrairement aux versions de Galileo et Newton) étaient les suivants:

• L'espace et le temps ne sont pas ce que vous pensez qu'ils sont. Différents observateurs se déplaçant uniformément les uns par rapport aux autres divergent dans leurs estimations de la longueur des objets et des intervalles de temps entre les événements (et ces écarts peuvent être mesurés avec précision).
• Il existe une limite de vitesse universelle, s; tout observateur mesurant la vitesse d'un objet par rapport à lui constatera que cette vitesse est inférieure ou égale à s.
• Dans un tel monde, certains champs - «champs relativistes» - peuvent exister sans médium, et ils satisfont des équations de mouvement spéciales. Le champ relativiste le plus simple satisfait les équations de mouvement des classes 0 ou 1, la vitesse d'onde cw mentionnée dans l'équation de mouvement prenant la valeur c.

En bref, il existe des champs relativistes de classe 0 satisfaisant l'équation

$$

$$Classe 0: \; d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = 0$$

La lumière, et toutes les ondes électromagnétiques, est l'exemple le plus célèbre, mais pas unique - par conséquent, "c" est souvent appelé la "vitesse de la lumière". Et il y a des champs relativistes de classe 1 satisfaisant l'équation

$$

$$Classe 1: \; d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = - (2 \ pi \ mu) ^ 2 (Z - Z_0)$$

Nous verrons leurs exemples dans le prochain article. Notez que la relativité n'impose pas de restrictions sur μ (sauf pour que μ ² soit positif) ou sur Z ₀ . Pour les champs relativistes, il existe des équations plus complexes, mais la plupart d'entre elles dans la description des processus physiques simples sont réduites à l'un de ces deux.

Les champs relativistes sont physiquement réels et ont une signification physique dans l'Univers, c'est-à-dire:

• Leurs ondes transportent de l'énergie et des informations d'un endroit à un autre.
• Les vagues dans un champ peuvent affecter un autre champ et changer les processus physiques qui auraient lieu en leur absence.

Mais, contrairement aux champs, dont des exemples sont donnés dans cet article, les champs relativistes ne décrivent la propriété d'aucun support physique ordinaire, consistant en quelque chose ressemblant à de la matière ordinaire, et, pour autant que cela soit expérimentalement connu, ils ne décrivent pas les propriétés de quoi que ce soit. quoi qu'il arrive. Ces domaines, peut-être, à notre connaissance aujourd'hui, sont l'un des éléments fondamentaux de l'Univers.