Nous comprenons la physique des particules: 7) les particules sont des quanta

1. Balle sur ressort, version newtonienne
2. Une boule quantique sur un ressort
3. Vagues, look classique
4. Les vagues, l'équation classique du mouvement
5. Ondes quantiques
6. Champs
7. Les particules sont des quanta
8. Comment les particules interagissent avec les champs

Donc, finalement, nous sommes arrivés à notre objectif: comprendre ce que ces choses que nous appelons des «particules» sont, en fait, des électrons, des photons, des quarks, des gluons et des neutrinos. Tout cela, bien sûr, s'applique à la science moderne. Il convient de rappeler qu'en science, rien ne garantit que la compréhension actuelle ne sera pas davantage approfondie.

L'article précédent décrivait ce que sont les champs - des objets qui ont un sens à n'importe quel point de l'espace et à n'importe quel moment du temps (fonctions de l'espace et du temps), satisfont l'équation du mouvement et sont physiquement significatifs du fait qu'ils sont capables de transférer de l'énergie d'un endroit à un autre et influencer les processus physiques de l'univers.

Nous avons appris que la plupart des domaines que nous connaissons décrivent une propriété d'un milieu, comme la hauteur d'une corde ou la pression dans un gaz. Mais nous avons également appris que dans la théorie de la relativité d'Einstein, il existe une classe spéciale de champs, les champs relativistes qui ne nécessitent pas de support. Ou du moins s'ils ont un environnement, c'est très inhabituel. Rien dans les équations de champ ne nécessite la présence d'un médium et n'indique quelle propriété de ce médium est décrite par les champs relativistes.

Donc pour l'instant, nous considérerons les champs relativistes comme des objets physiques élémentaires de l'univers, et non comme certaines propriétés d'un milieu inconnu. Si un tel point de vue sera soutenu davantage par les physiciens - le temps nous le dira.

Nous avons considéré deux classes de champs relativistes et nous allons maintenant les étudier plus en détail. Ils satisfont soit à l'équation de mouvement de classe 0, où c _w = c (où c est la limite de vitesse universelle, souvent appelée «vitesse de la lumière»).

$$

$$d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = 0$$

Ou équations de mouvement de classe 1, où cw = c

$$

$$d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = - (2 \ pi \ mu) ^ 2 (Z - Z_0)$$

Dans l'article précédent, il a été montré que μ est la fréquence d'onde minimale dans de tels champs. Dans cet article, nous le désignerons par ν _min .

Pourquoi la limite de vitesse universelle est-elle souvent appelée vitesse de la lumière? Les vagues avec une équation de classe 0 se déplacent avec la vitesse c _w . La lumière (un terme général désignant les ondes électromagnétiques de toute fréquence) se déplaçant dans un espace vide satisfait l'équation relativiste de la classe 0, donc les ondes de lumière (et les ondes de tout champ relativiste satisfaisant l'équation relativiste de la classe 0) se déplacent avec la vitesse c.

De plus, dans le même article, nous avons vu que si un champ de classe 1 a une onde d'amplitude A, de fréquence ν, de longueur d'onde λ et d'état d'équilibre Z ₀ , alors l'équation du mouvement nécessite que la fréquence et la longueur d'onde soient liées à μ = ν _min apparaissant dans les équations par la formule

$$

$$\ nu ^ 2 = (c / \ lambda) ^ 2 + \ mu ^ 2 = (c / \ lambda) ^ 2 + \ nu_ {min} ^ 2$$

Il s'agit d'une formule pythagoricienne - elle peut être représentée, si vous le souhaitez, sous la forme d'un triangle, comme sur la Fig. 1. La fréquence minimale de toute onde est ν _min , et l'affectation ν = ν _min (et donc, comme λ → ∞) correspond à la compression du triangle en une ligne verticale (Fig. 1, ci-dessous). Vous pouvez également obtenir une relation similaire de classe 0 en faisant μ = ν _min zéro. Ensuite, vous pouvez extraire la racine carrée et obtenir

$$

$$\ nu = c / \ lambda$$

Il s'agit d'un triangle compressé en une ligne horizontale (Fig.1, à droite). Dans ce cas, la fréquence minimale est nulle. Le champ peut fluctuer arbitrairement lentement.


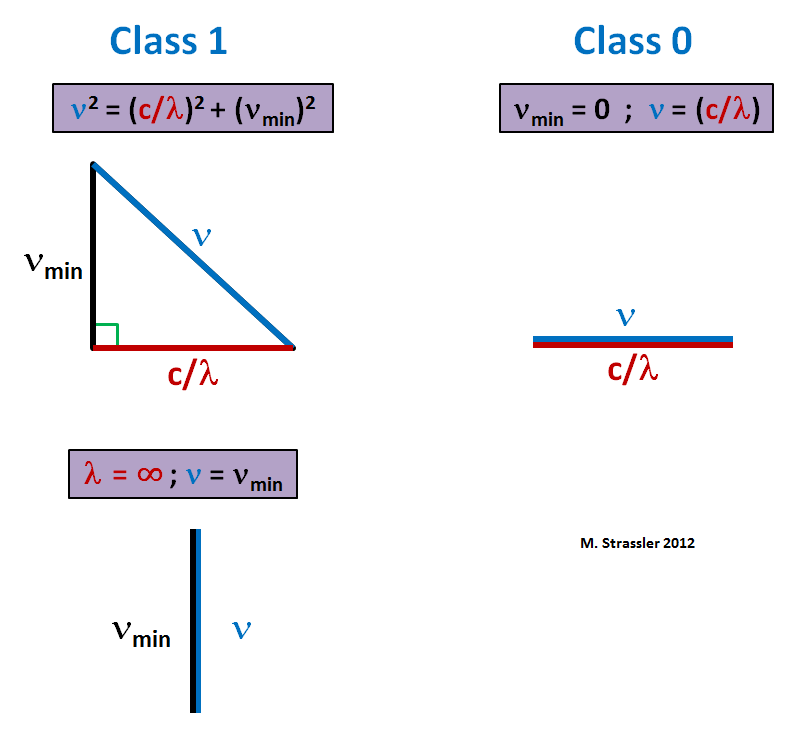Fig. 1

Il n'y a aucune restriction sur A. Mais c'est parce que nous ignorons la mécanique quantique. Le moment est venu d'étudier les champs quantiques relativistes.

Champs quantiques relativistes

Le monde réel est quantique-mécanique, donc l'amplitude A ne peut être nulle. Il prend des valeurs discrètes proportionnelles à la racine carrée de n, un entier non négatif indiquant le nombre de quanta de vibration dans l'onde. L'énergie stockée dans la vague est

$$

$$E = (n + 1/2) h \ nu$$

Où h est la constante de Planck, apparaissant nécessairement là où la mécanique quantique est importante. En d'autres termes, l'énergie associée à chaque quantum d'oscillations ne dépend que de la fréquence des oscillations de l'onde, et est égale à

$$

$$E = h \ nu$$

Ce rapport a été proposé pour la première fois, spécifiquement pour les ondes lumineuses, par Einstein en 1905, dans son explication de l'effet photoélectrique.

Mais rappelons-nous notre rapport pythagoricien de fréquence et de longueur d'onde. Si nous le multiplions par h ² , nous obtenons cela pour un champ quantique de classe 1

$$

$$E ^ 2 = (h \ nu) ^ 2 = (h c / \ lambda) ^ 2 + (h \ nu_ {min}) ^ 2 \ quad (*)$$

Cela semble familier. Nous savons déjà que tout objet de la théorie de la relativité d'Einstein doit satisfaire l'équation décrivant son énergie, sa quantité de mouvement et sa masse:

$$

$$E ^ 2 = (pc) ^ 2 + (mc ^ 2) ^ 2$$

Une autre relation pythagoricienne. L'énergie minimale de l'objet est mc ² , ce qui ressemble à l'énoncé de la fréquence minimale qu'une onde de classe 1, ν _min , peut posséder. On peut être tenté de supposer que, probablement, pour un quantum d'un champ relativiste

$$

$$p c = h c / \ lambda \ quad (**)$$

$$

$$m c ^ 2 = h \ nu_ {min} \ quad (***)$$

La première équation est apparue pour la première fois dans les travaux de Louis De Broglie en 1924 - près de 20 ans après Einstein. Pourquoi a-t-il fallu si longtemps? Je ne sais pas.


Fig. 2

Est-ce que cela a du sens? Comme nous l'avons noté, les champs relativistes de classe 0 incluent également les champs électriques et leurs ondes sont des ondes électromagnétiques, c'est-à-dire de la lumière. La version de la formule (*) que nous obtenons pour les quanta de classe 0 est la même que pour les champs de classe 1 pour lesquels μ = ν _{min est} égal à zéro - c'est-à-dire m = 0. Nous extrayons la racine carrée et obtenons

$$

$$E = p c$$

Ou l'équation d'Einstein pour les particules sans masse. Et les quanta des ondes électromagnétiques (y compris tous les types de lumière: visible, ultraviolet, infrarouge, ondes radio, rayonnement gamma, etc., ne différant que par la fréquence, et donc l'énergie des quanta) seront vraiment des particules sans masse - dès que nous appliquons l'indication indiquée au-dessus de quelques équations (**) et (***). Ce sont des photons.

À partir de l'équation (***), nous pouvons enfin calculer la masse de la particule. Chaque particule ayant une masse est un quantum d'un champ de classe 1. La fréquence minimale de ces ondes est ν _min . L'énergie minimale d'un quantum d'une telle onde est égale à h fois la fréquence. Et la masse de la particule est simplement l'énergie minimale divisée par c ² .

$$

$$m = h \ nu_ {min} / c ^ 2$$

Si nous voulons comprendre d'où vient la masse des particules, nous devons comprendre ce qui détermine ν _min et pourquoi il y a une fréquence minimale en général. Pour les particules telles que les électrons et les quarks, cela n'est pas du tout clair, mais on sait que le champ de Higgs joue un rôle important à cet égard.

Nous concluons: les particules de la nature sont des quanta de champs quantiques relativistes. Les particules sans masse sont des quanta d'ondes de champ satisfaisant une équation de classe 0. Celles qui possèdent une masse correspondent aux champs d'une équation de classe 1. Il y a beaucoup de détails, mais ce fait est l'une des propriétés fondamentales fondamentales de notre monde.

Ces quanta se comportent-ils vraiment comme des particules?

Nous imaginons les particules comme des particules de poussière ou des grains de sable. En ce sens, les quanta ne sont pas des particules - ce sont des ondes qui ont une énergie et une amplitude minimales pour une certaine fréquence. Mais ils se comportent tellement comme des particules que l'on peut pardonner d'utiliser le mot «particule» dans leur description. Voyons pourquoi.

Si vous prenez une vague dans l'eau et la laissez passer à travers des pierres peu profondes sous la surface, une partie de la vague traversera la ligne de pierres et une partie sera réfléchie, comme le montre la Fig. 3. La partie de l'onde qui traversera la ligne dépend de la forme des pierres, de leur proximité avec la surface, etc. Mais l'essentiel est qu'une partie de l'onde est transmise à travers les pierres, et une partie sera réfléchie. Une partie de l'énergie des vagues ira dans la même direction, une partie ira dans la direction opposée.


Fig. 3

Mais si vous envoyez un photon vers le verre réfléchissant, ce photon le traversera ou sera réfléchi (Fig.4). Plus précisément, si vous mesurez le comportement d'un photon, vous saurez s'il est réfléchi ou transmis. Si vous ne mesurez pas, il sera impossible de dire ce qui s'est passé. Bienvenue dans le marais de la mécanique quantique. Un photon est un quantum. Son énergie ne peut pas être divisée en la partie qui a traversé le verre et la partie qui a été réfléchie - car alors de chaque côté il y aura moins d'un quantum, ce qui est interdit. (Petits caractères: le verre ne change pas la fréquence des photons, donc l'énergie ne peut pas être divisée entre deux quanta ou plus de fréquences plus basses). Ainsi, le photon, bien qu'il s'agisse d'une onde, se comporte comme une particule dans ce cas. Il se reflète sur le verre ou non. Qu'elle soit réfléchie ou non, la mécanique quantique ne le prédit pas. Il ne donne que la probabilité de réflexion. Mais elle prédit que quoi qu'il arrive, le photon voyagera comme une unité et conservera son identité.


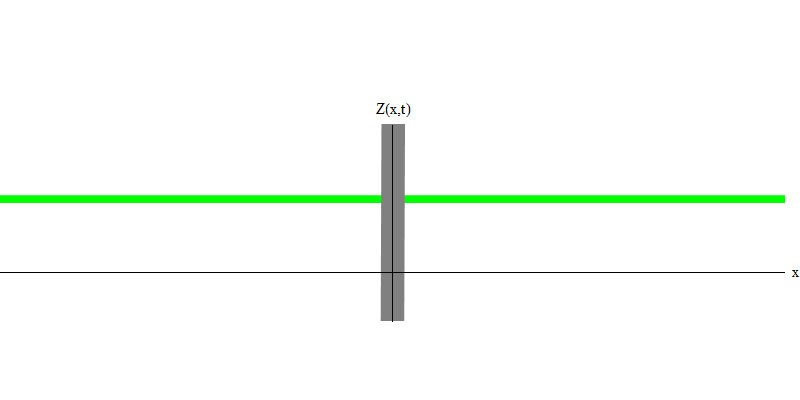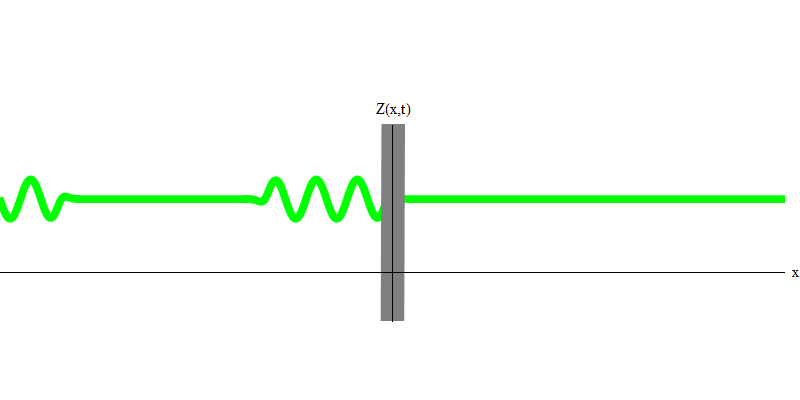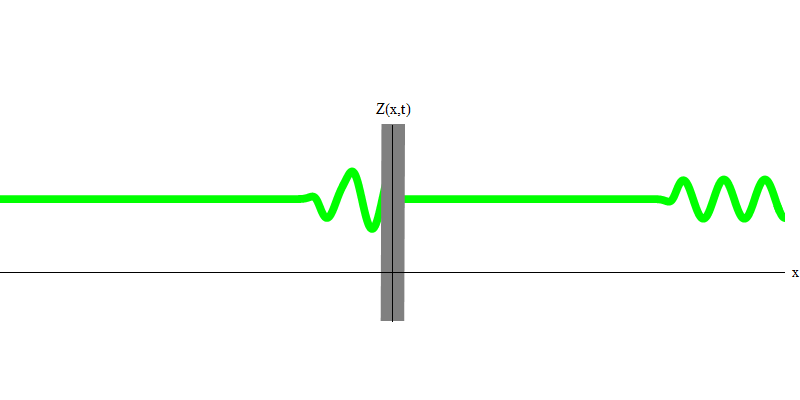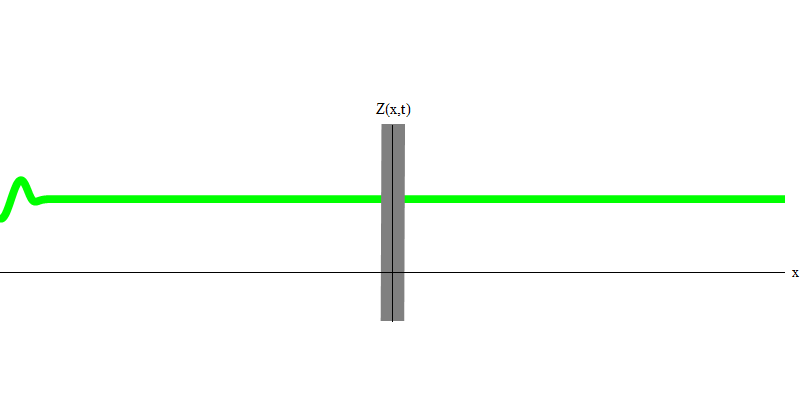Fig. 4

Et qu'arrivera-t-il aux deux photons? Ça dépend. Par exemple, si des photons sont émis à différents moments de différents endroits, l'observateur verra alors deux quanta, séparés dans l'espace et se déplaçant probablement dans des directions différentes (Fig. 5). Ils peuvent avoir des fréquences différentes.


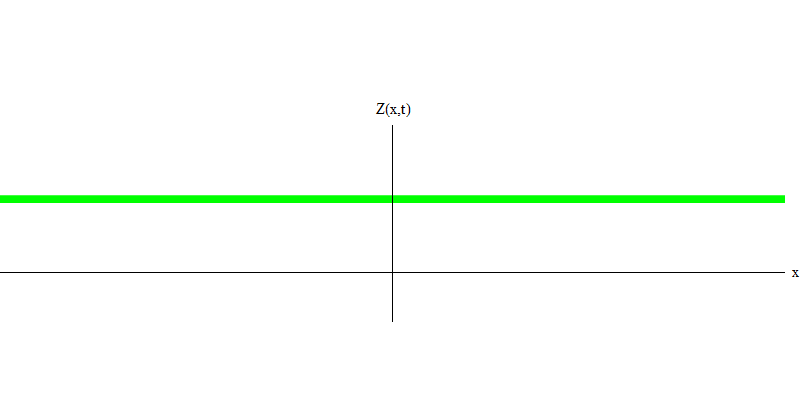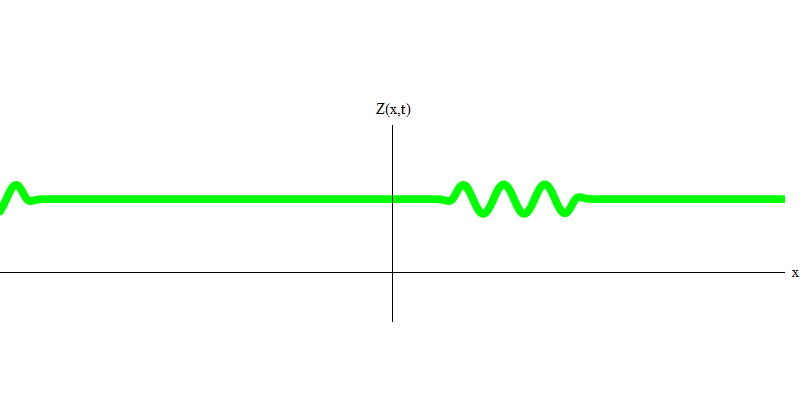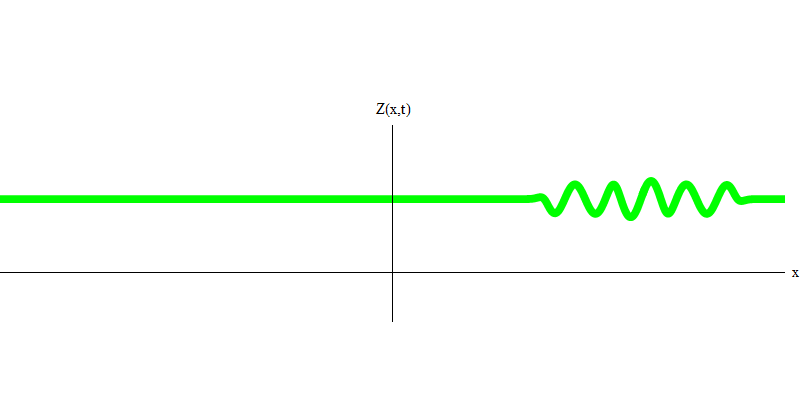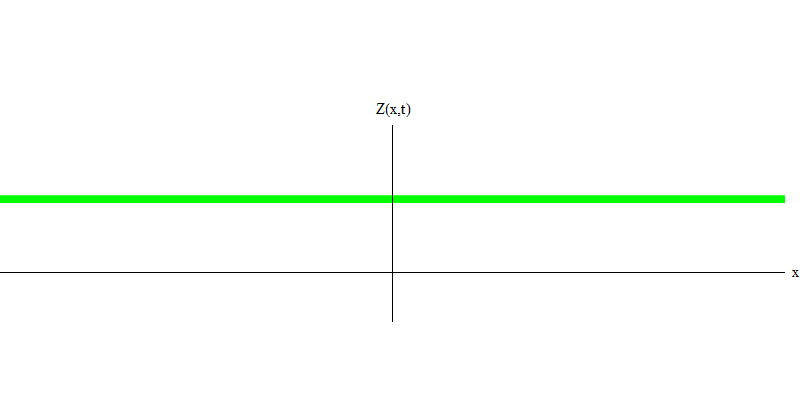Fig. 5: quanta indépendant

Dans le cas particulier, lorsque deux photons sont émis ensemble et parfaitement synchroniquement (comme dans les lasers), ils se comportent comme indiqué sur la Fig. 6. Si nous envoyons une combinaison de deux photons dans le verre, alors pas deux, mais trois choses peuvent se produire. Soit les deux photons passeront à travers le verre, soit les deux seront réfléchis, soit l'un passera et l'autre sera réfléchi. 0, 1 ou 2 photons seront réfléchis par le verre - il n'y a pas d'autres options. Dans ce sens, les quanta légers se comportent à nouveau comme des particules, comme de petites boules - si vous jetez deux boules dans une grille qui a des trous, alors 0, 1 ou 2 boules seront réfléchies par la grille, et 0, 1 ou 2 boules passeront par les trous . Il n'y a aucune possibilité que 1 538 buts se reflètent sur le net.


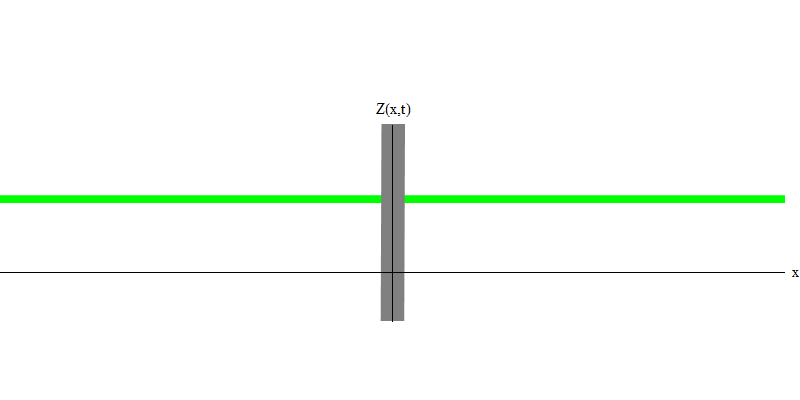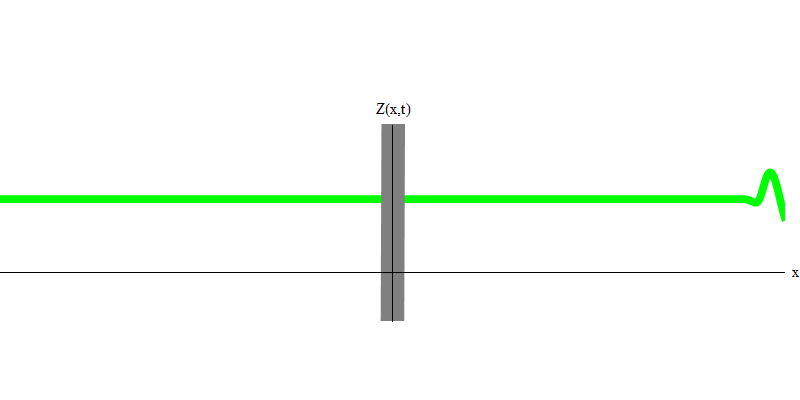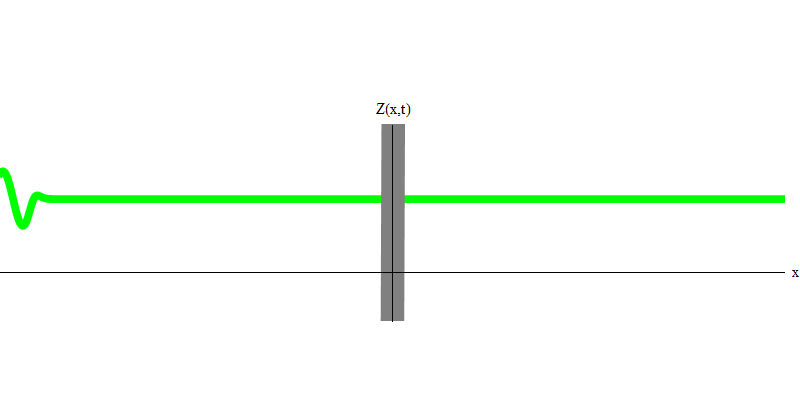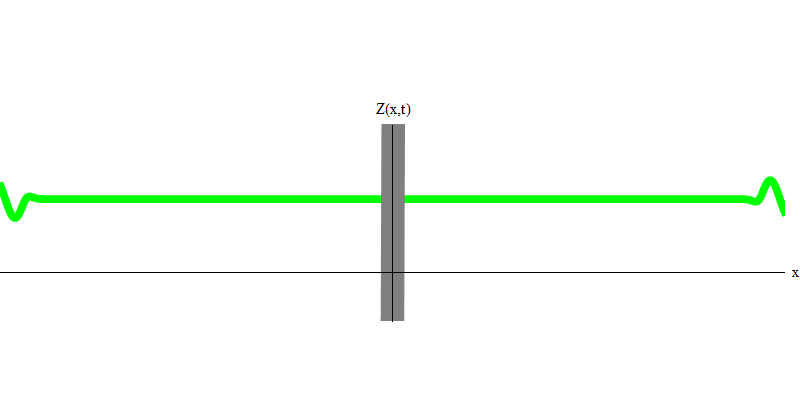Fig. 6

Mais ce sont des photons qui, sans masse, sont obligés de se déplacer à la vitesse de la lumière et E = p c. Qu'en est-il des particules de masse comme les électrons? Les électrons sont des quanta du champ électrique et, comme les photons, ils peuvent être émis, absorbés, réfléchis ou transmis dans leur ensemble. Ils ont une certaine énergie et un certain élan, $$$E ^ 2 = (pc) ^ 2 + (m_e c ^ 2) ^ 2$ où m _e est la masse de l'électron. La différence entre les électrons et les photons est qu'ils se déplacent plus lentement que la lumière et peuvent donc se reposer. L'esquisse d'un tel événement (en mécanique quantique, en raison du principe d'incertitude, rien ne peut être vraiment statique) d'un électron stationnaire est donnée dans la Fig. 7. Il s'agit d'une onde de fréquence minimale obtenue en attribuant une longueur d'onde d'une valeur très grande, presque infinie. Par conséquent, la forme d'onde spatiale de la Fig. ne montre aucune circonvolution - elle fluctue simplement dans le temps.


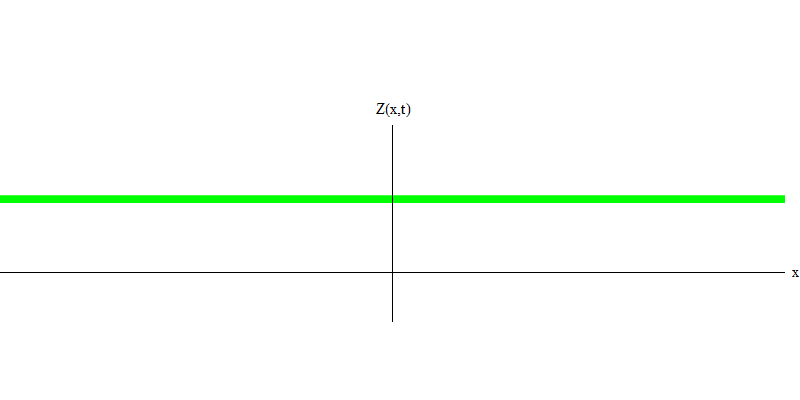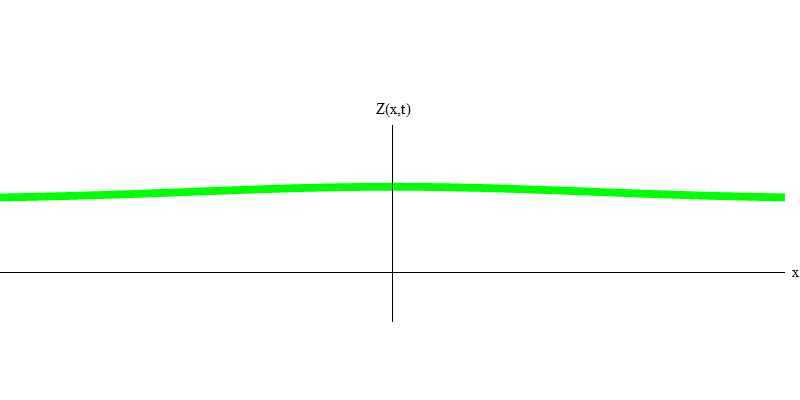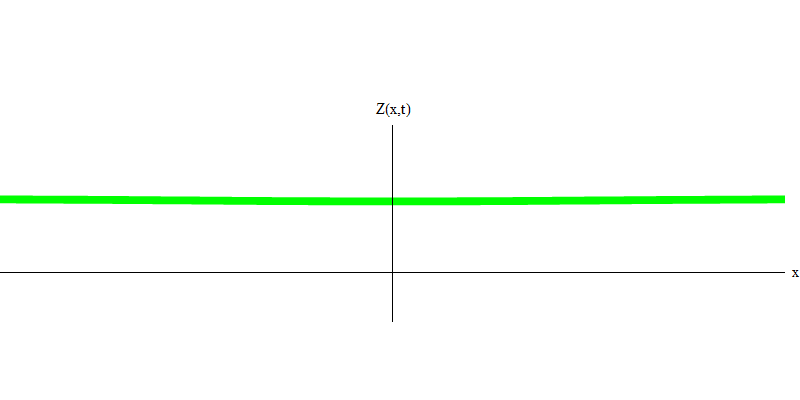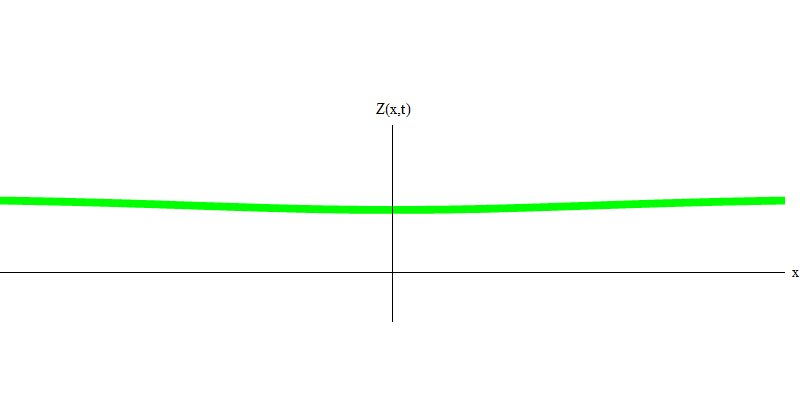Fig. 7

Donc, oui, en fait, les quanta se comportent très bien comme des particules, et donc appeler des électrons, des quarks, des neutrinos, des photons, des gluons, des particules W et des particules de Higgs "particules" ne sera pas une déception catastrophique. Mais le mot «quantique» est mieux adapté à cela - car ce sont précisément des quanta.

En quoi les fermions et les bosons diffèrent-ils les uns des autres?

• Toutes les particules élémentaires sont divisées en fermions et bosons.
• Les fermions (y compris les électrons, les quarks et les neutrinos) satisfont au principe d'exclusion de Pauli - deux fermions du même type ne peuvent pas faire la même chose.
• Les bosons (y compris les photons, les particules W et Z, les gluons, les gravitons et les particules de Higgs) sont différents: deux bosons ou plus du même type peuvent faire la même chose.

C'est pourquoi les lasers peuvent être constitués de photons - car ce sont des bosons, ils peuvent être dans le même état et générer un puissant rayon d'une lumière. Mais un laser ne peut pas être constitué d'électrons qui sont des fermions.

Comment cette différence se manifeste-t-elle dans le langage des mathématiques? Il s'avère que les formules que j'apporte conviennent aux bosons et aux fermions, elles doivent être changées - légèrement, mais avec de grandes conséquences. Pour les bosons, nous aurons:

$$

$$E = (n + 1/2) h \ nu, \ quad où \; n = 0, 1, 2, 3, 4, ...$$

Ce qui signifie que l'énergie de chaque quantum est égale à h ν. Cela implique que les quanta boson peuvent faire la même chose; lorsque n est supérieur à 1, l'onde dans le champ bosonique sera constituée de plusieurs quanta oscillant et se déplaçant ensemble. Mais pour les fermions:

$$

$$E = (n - 1/2) h \ nu, \ quad où \; n = 0 \; ou \; 1$$

L'énergie d'un quantum est toujours égale à h ν, de sorte que toute la discussion sur les particules et leurs énergies, impulsions et masses reste valable. Mais le nombre de quanta dans une onde électronique ne peut être que de 0 ou 1. Dix électrons, contrairement à dix photons, ne peuvent pas être organisés en une seule onde de plus grande amplitude. Par conséquent, il n'y a pas d'ondes de fermions composées d'un grand nombre de fermions oscillant et se déplaçant ensemble.