Nous comprenons la physique des particules: 8) comment les particules interagissent avec les champs

Comprendre la physique des particules:
1. Balle sur ressort, version newtonienne
2. Une boule quantique sur un ressort
3. Vagues, look classique
4. Les vagues, l'équation classique du mouvement
5. Ondes quantiques
6. Champs
7. Les particules sont des quanta
8. Comment les particules interagissent avec les champs

Comment fonctionne le champ Higgs:
1. L'idée principale

Dans un article précédent de la série, j'ai expliqué que les particules de la nature sont des quanta de champs relativistes qui satisfont aux équations de mouvement de la classe 0 et de la classe 1. Mais ce que je n'ai pas dit jusqu'à présent, cette affirmation, heureusement, n'est que partiellement vraie. Les équations réelles sont toujours un peu plus complexes, de sorte que l'interconnexion des particules et des champs demeure, mais des phénomènes et des processus beaucoup plus divers deviennent possibles, y compris l'apparition de particules après la collision d'autres particules, la désintégration des particules en d'autres particules et la dispersion des particules les unes des autres, ainsi que la formation d'objets intéressants tels que les protons et les neutrons, les noyaux atomiques et les atomes. Je ne serai pas en mesure d'expliquer tout cela en détail, mais dans cet article, je vais vous donner une introduction à la façon dont tout cela fonctionne.

La principale différence entre les équations, que j'ai appelées "classe 0" et "classe 1", et les équations qui sont significatives pour la physique réelle, c'est que dans les équations réelles, il existe des termes supplémentaires qui dépendent de deux ou plusieurs champs, et pas d'un seul . Autrement dit, au lieu d'une équation de classe 0 pour un champ relativiste Z (x, t), qui ressemble à

$$

$$d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = 0$$

pour les champs réels, les équations ressemblent plus à ceci:

$$

$$d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = y ’Z (x, t) ^ 3 + y A (x, t) B (x, t)$$

Où y et y 'sont des nombres (généralement inférieurs à 1), Z est une courte notation de Z (x, t), et A (x, t) et B (x, t) sont une paire d'autres champs. Dans de telles équations, on peut s'attendre à l'apparition de termes tels que A (x, t) Z (x, t), ou A (x, t) ² Z (x, t), ou Z (x, t) ² , ou même A (x, t) d ² Z / dt ² , etc. Les membres qui peuvent et ceux qui ne peuvent pas apparaître dépendent des détails des champs impliqués dans le processus. Les règles sont strictes, mais plutôt déroutantes, nous ne les aborderons donc pas pour l'instant. En général, à partir d'expériences, nous avons établi (et compris d'un point de vue théorique) que, dans la nature:

• Tout terme valable en principe (conservation de la charge électrique ou correspondance de la relativité d'Einstein) apparaît dans les équations,
• mais les membres avec de nombreux champs sont généralement très petits et insignifiants par rapport aux membres avec un, deux et parfois trois champs (les membres avec des dérivées du temps ou de l'espace sont également généralement petits).

Par conséquent, dans les processus physiques les plus intéressants, on peut se concentrer sur tous les termes valides avec un, deux ou trois champs.

Un peu de terminologie. Les termes dans les équations aux champs sont appelés linéaires au premier degré. Tous les termes de nos équations de classe 0 ou 1 étaient linéaires. Les membres à deux ou trois champs sont appelés quadratiques ou cubiques; en général, ils sont appelés non linéaires. Tous les phénomènes intéressants de notre monde apparaissent en raison de termes non linéaires dans les équations du mouvement - à savoir, l'interaction des champs entre eux et avec eux-mêmes. Étudions l'un d'eux.

L'émergence d'une nouvelle vague de la résonance des deux autres

Pour avoir une idée de la façon dont tout peut devenir intéressant, nous prenons trois champs, A (x, t), B (x, t), C (x, t), et une situation simplifiée. Supposons que les champs A et B satisfassent approximativement les équations de classe 0 (et contiennent des quanta sans masse), et que le champ C satisfasse les équations de classe 1 (contient des ondes avec une fréquence minimale ν _min et, par conséquent, des quanta de masse m = h ν _min / c ² , où h - constante de Planck). Nous ajouterons également des termes non linéaires à leurs équations. Plus précisément, comme ceci (par souci de concision, nous écrirons «A» au lieu de «A (x, t)», etc., c est la vitesse de la lumière, y est un nombre qui est généralement inférieur à 1):

$$

$$d ^ 2A / dt ^ 2 - c ^ 2 d ^ 2A / dx ^ 2 = y BC \\ d ^ 2B / dt ^ 2 - c ^ 2 d ^ 2B / dx ^ 2 = y AC \\ d ^ 2C / dt ^ 2 - c ^ 2 d ^ 2C / dx ^ 2 = (2 \ pi \ nu_ {min}) ^ 2 C + y AB$$

Petits caractères: J'ai ajouté des termes non linéaires aux trois équations parce que la présence de tels termes dans l'une des équations et leur absence dans l'autre entraînera des contradictions; par exemple, l'énergie ne sera pas conservée. Pour le processus que je décris, nous n'aurons besoin de considérer que des termes non linéaires dans les équations de mouvement du champ C.

Voyons ce qui se passe avec un tel ensemble d'équations si l'onde du champ A rencontre l'onde du champ B. En principe, nous pouvons le deviner en appliquant la méthode de l'examen attentif. S'il y a une onde dans le champ A, alors A (x, t) est non nul près de lui. Lorsque les vagues des champs A et B se chevauchent, le résultat de la multiplication de A (x, t) et B (x, t) devient non nul. Passons maintenant à l'équation pour C: les changements dans le champ C dans le temps et l'espace (deux termes sur le côté gauche) sont associés au produit A et B (l'un des termes sur le côté droit).

$$

$$d ^ 2C / dt ^ 2 - c ^ 2 d ^ 2C / dx ^ 2 = (2 \ pi \ nu_ {min}) ^ 2 C + y A B$$

Ainsi, même si le champ C est nul lorsque A (x, t) B (x, t) devient non nul, alors C (x, t) deviendra bientôt non nul dans la même section. Bref, suite à la rencontre des ondes A et B, une certaine petite perturbation du champ C se produira.

Petits caractères: vous pouvez être intéressé par - après que C soit non nul, si le terme A (x, t) C (x, t) devient dans l'équation de mouvement pour le champ. Cela provoque une perturbation supplémentaire du champ B. La réponse est oui, mais cet effet encore plus petit. Jusqu'à ce que nous l'ignorions et que nous découvrions plus tard pourquoi cela en valait la peine.

Dans la fig. La figure 1 montre une onde de fréquence ν dans le champ A (vert), qui se produit avec une onde de fréquence ν dans le champ B (bleu). J'ai égalisé les fréquences pour plus de simplicité et de symétrie. Plus tard, nous verrons pourquoi d'autres cas se résument à cela. La vitesse ν peut être estimée en observant l'onde verte et la ligne verticale situées en un point de l'espace et oscillant avec l'onde.

Le produit orange ci-dessous montre le produit A (x, t) B (x, t); on peut voir qu'elle devient non nulle lorsque deux ondes se superposent. On voit également qu'elle varie dans le temps. Vous pouvez voir (en le comparant à une barre verticale oscillante) que A (x, t) B (x, t) oscille deux fois plus vite. Rappelez-vous ce fait important. Dans le cas général, si une onde de fréquence ν ₁ rencontre une onde de fréquence ν ₂ , alors leur produit oscillera avec une fréquence ν ₁ + ν ₂ . Et encore une chose: vous pouvez remarquer que les vibrations AB ne se déplacent pas à droite ou à gauche, elles restent en place. Plus tard, nous verrons pourquoi c'est important.


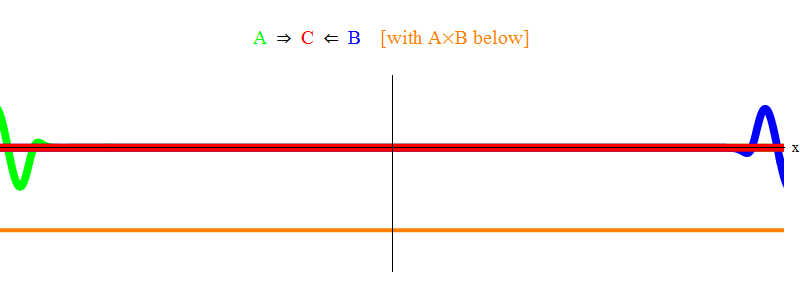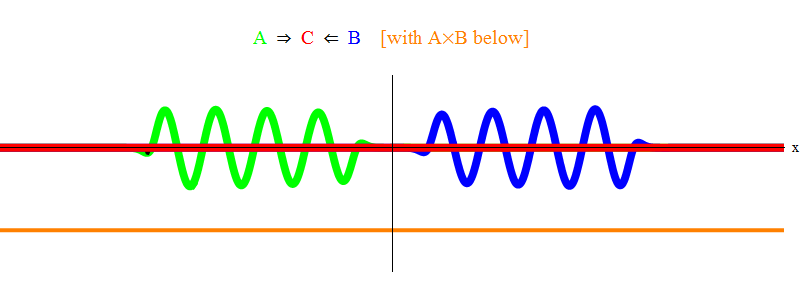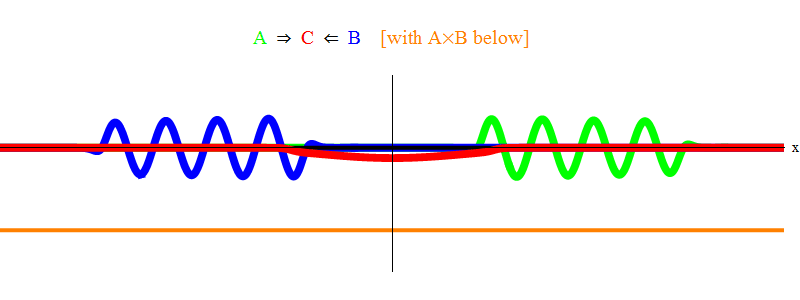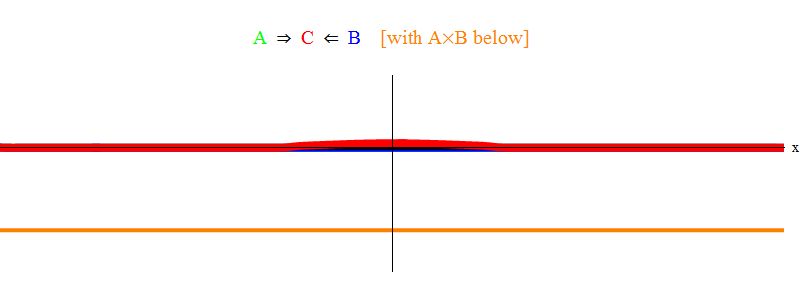Fig. 1

Comment une valeur non nulle de AB affecte-t-elle C? La réponse dépend fortement de la fréquence ν. Je vais d'abord vous donner une réponse toute prête, puis une explication approximative de la raison. C'est, en fait, une résonance . La résonance est un phénomène intégral de toutes les vibrations (vibrations), y compris les ondes. J'ai déjà décrit comment la balle sur le ressort oscille avec une fréquence naturelle et comment la force vibratoire poussant la balle peut conduire à une résonance si la fréquence d'oscillation de la force coïncide avec la fréquence naturelle de la balle sur le ressort.

Après avoir compris la résonance, vous verrez que le champ C, oscillant avec une fréquence minimale et une vitesse horizontale nulle, se comporte comme une balle sur un ressort, et AB se comporte comme une force oscillante essayant de faire osciller la balle. Par conséquent, le phénomène de résonance se produit si la fréquence de vibration AB - 2ν - est la fréquence minimale du champ C - ν _min . Plus précisément:

• Si 2 ν n'est pas égal à ν _min - si la force n'est pas en résonance - alors dans la zone où AB n'est pas égal à zéro, C commencera à fluctuer irrégulièrement, avec une petite amplitude.
• Si 2 ν = ν _min - si la force est en résonance - alors C oscillera doucement, avec une grande amplitude, dans la zone où AB n'est pas égal à zéro, et continuera de fluctuer même lorsque AB redeviendra nul.

Fig. 1 ne montre que la situation résonante 2 ν = ν _min . On voit que lorsque l'onde A traverse l'onde B, elles laissent derrière elles une onde stationnaire C, oscillant avec une fréquence ν _min . Copie fine: dans la fig. un croquis est montré, pas une solution exacte des équations. La solution exacte aura de nombreuses petites fonctionnalités complexes qui occultent la signification physique de base, je les ai donc supprimées pour plus de clarté. Plus tard, nous considérerons une situation sans résonance, ce qui est beaucoup plus compliqué, mais aussi plus important pour la physique.

L'émergence d'une nouvelle particule de l'anéantissement des deux autres

Je viens de vous démontrer que les termes non linéaires AB dans l'équation C peuvent provoquer la superposition des ondes A et B pour produire des oscillations du champ C si la somme des fréquences des champs A et B est égale à la fréquence minimale du champ C. Mais que faire si ces ondes avaient très petite amplitude? Que peut-il se passer si un quantum du champ A rencontre un quantum du champ B?

• Si les fréquences AB entrent en résonance avec le champ C, alors un quantum de champ C peut se produire, c'est-à-dire une vraie particule C, et les quanta A et B disparaîtront - «annihiler».
• De plus, les quanta A et B peuvent simplement se croiser sans créer de particule C.
• Les lois de la mécanique quantique suggèrent que la probabilité de créer une particule C est proportionnelle au carré de y, qui est multiplié par AB dans l'équation du mouvement C.
• Si les fréquences n'entrent pas dans la résonance, la vraie particule C n'apparaîtra pas. Cependant, une perturbation temporaire peut se produire dans le champ C, un exemple de ce qu'on appelle souvent la «particule virtuelle» C, auquel cas les quanta A et B peuvent disparaître. Quel est le résultat d'une telle perturbation? J'ai partiellement décrit ce processus à la fin de l'article, dans la section «queues».

Tel est l'état général des choses. Plongeons-nous dans les détails.

Que signifie pour les particules, c'est-à-dire les quanta des champs A, B et C, être en résonance ou non en résonance? Il convient de rappeler que l'énergie d'un quantum est liée à sa fréquence en raison de l'équation E = h ν. Nous traduisons donc notre discussion sur les ondes en une discussion sur les particules.

Supposons que nos ondes dans les champs A et B se composent chacune d'un quantum. Ces quanta sont sans masse, puisque A et B satisfont aux équations de classe 0. Plus précisément, les termes linéaires dans leurs équations de mouvement sont les mêmes que les équations de classe 0. Puisque les quanta A et B ont la même fréquence, ils ont la même énergie, E = h ν. Puisque l'impulsion d'un quantum sans masse est p = E / c, les quanta A et B auront des impulsions de magnitude égale à h ν / c, mais de sens opposé, car l'un d'eux se déplace vers la gauche et l'autre vers la droite. Par conséquent:

• L'énergie totale de deux quanta ensemble sera de 2 heures.
• La quantité de mouvement totale des deux quanta ensemble sera nulle.

Étant donné que l'énergie et la quantité de mouvement sont conservées, l'énergie totale après la collision de deux quanta restera égale à 2 heures et le moment total restera nul.

Dans le cas des vagues, nous avons vu que puisque l'équation pour C contient un terme de la forme AB, il y a une résonance lorsque la fréquence AB (fonctionnant comme une force oscillante) coïncide avec la fréquence minimale C (fonctionnant comme une boule sur un ressort). Nous traduisons cette affirmation en quanta.

La fréquence AB sera de 2 ν, donc l'énergie des produits A et B, lorsque les ondes A et B sont constituées d'un quantum, est égale à la somme des énergies A et B.

$$

$$E_ {AB} = 2 h \ nu = E_A + E_B$$

La fréquence minimale C est égale à ν _min , ce qui signifie que pour un quantum stationnaire du champ C, l'impulsion est 0 et l'énergie

$$

$$E_C = h \ nu_ {min} = mc ^ 2$$

Où m est la masse du quantum C.

Pour la résonance, 2 ν = ν _min sont nécessaires, c'est-à-dire:

$$

$$E_A + E_B = 2 h \ nu = h \ nu_ {min} = mc ^ 2 = E_C$$

En bref, la résonance se produit lorsque les sommes d'énergies égales des particules A et B (dans lesquelles dans notre cas les impulsions sont de même amplitude et de sens opposé) sont juste suffisantes pour créer une particule stationnaire C! Dans le processus, les particules A et B sont annihilées - leur énergie va complètement dans la création de la particule C. Ceci est illustré (schématiquement) sur la Fig. 2, que vous devez comparer avec la fig. 1.


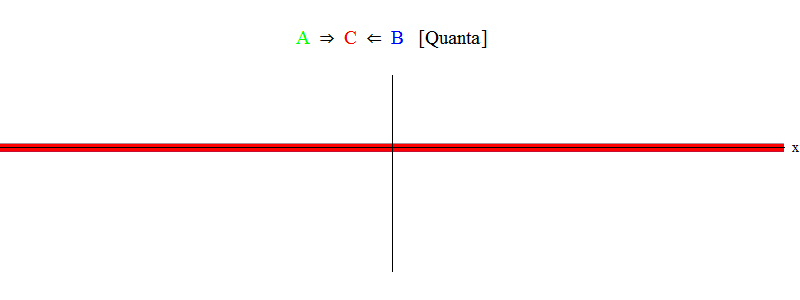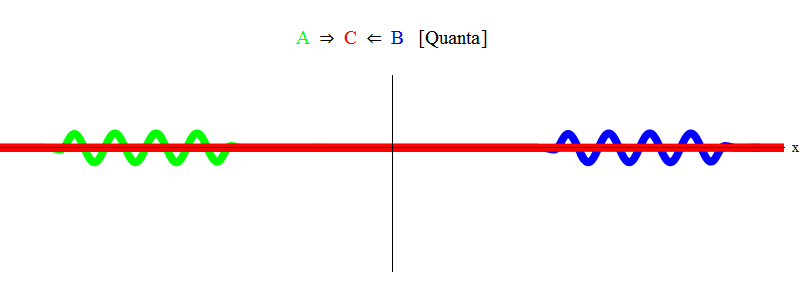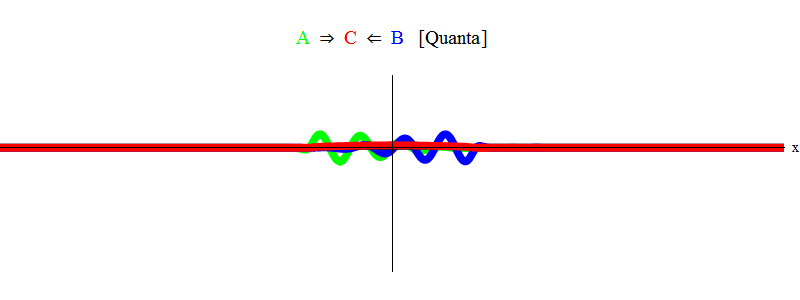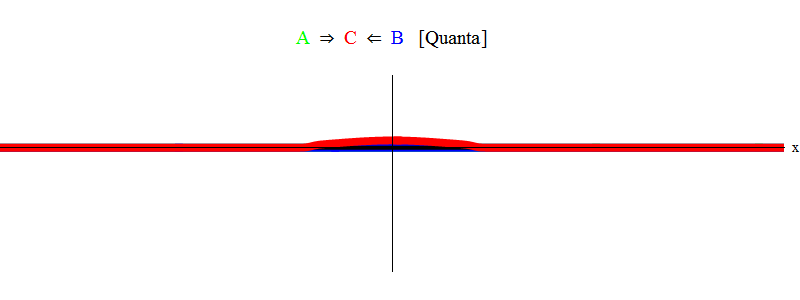Fig. 2

Raisonnement

Je viens de vous montrer le processus A + B → C. Dans mon explication, j'ai utilisé trois types de particules différents pour éviter toute confusion. Mais la même idée permet de passer par des processus de la forme A + A → C (par exemple, gluon + gluon → la particule de Higgs, et c'est essentiellement ainsi que la particule de Higgs est obtenue dans le grand collisionneur de hadrons) et des processus de la forme A + A * → C, où A * - antiparticule pour A (par exemple, quark + antiquark → particule Z, et c'est ainsi que les particules Z sont généralement obtenues sur le LHC). Il suffit de modifier des détails mineurs, mais l'essence reste la même.

Un autre processus qui représente la même idée, seulement inversé dans le temps - la désintégration des particules. La désintégration d'une particule de Higgs en deux photons ou particules Z en un quark et un antiquark se produit essentiellement comme l'animation de la Fig. 2, en allant dans la direction opposée.

Queues

1. Si le terme AB perturbe le champ C sans résonance - si 2 ν ≠ ν _min - que se passera-t-il? Vous vous souvenez peut-être que si vous poussez la balançoire avec l'enfant à la mauvaise fréquence ou appliquez une force à la balle sur le ressort, oscillant avec une fréquence qui ne coïncide pas avec la fréquence naturelle des vibrations, vous obtiendrez une vibration inégale avec une petite amplitude. Dans le contexte actuel, la même chose se produit avec le champ C. Le champ C se comportera d'une manière ou d'une autre, mais cela n'entraînera pas l'apparition d'un quantum C. qui se comporte bien. Il devient juste un peu inquiet. Cette mauvaise indignation est un exemple de la soi-disant «Particules virtuelles C» - mais ce n'est pas une particule (quantum d'une onde de champ C), malgré son nom. Sa masse est différente de la masse de la particule C; il peut être plus grand ou plus petit. Contrairement à la particule C, elle n'existe pas d'elle-même depuis longtemps. Et il ne satisfait pas aux conditions d'amplitude que les vrais quanta doivent satisfaire. Au contraire, contrairement à la particule C, qui existe depuis un certain temps, avec la fig. 2, une perturbation non résonnante n'existe que lorsque A coupe B.

Mais cela ne signifie pas que cela n'affecte rien. Par exemple, cela peut faire rebondir les particules A et B.

$$

$$A_ \ rightarrow + B_ \ leftarrow → C_ {outrage} → A_ \ leftarrow + B_ \ rightarrow$$

En général, dans un espace tridimensionnel, un rebond ou une diffusion peut conduire au fait que A se déplace dans n'importe quelle direction et B se déplace dans la direction opposée. Des exemples de tels processus comprennent la diffusion d'électrons et de positrons due à un photon virtuel, ou la diffusion de quarks et d'antiquark due à un gluon virtuel.

En présence d'autres champs, D et E, interagissant avec C et participant à l'équation du mouvement C

$$

$$d ^ 2C / dt ^ 2 - c ^ 2 d ^ 2C / dx ^ 2 = (2 \ pi \ nu_ {min}) ^ 2 C + y A B + y ’D E$$

Des processus beaucoup plus intéressants peuvent se produire:

A + B → _perturbation C → D + E

C'est vrai: les particules A et B peuvent s'annihiler grâce à la particule virtuelle C, et conduire à l'apparition de nouvelles particules D et E. C'est la deuxième façon de créer de nouvelles particules! Par exemple, un électron peut entrer en collision avec un positron, s'annihiler à travers un photon virtuel (rappelez-vous que cela signifie «par une perturbation du champ de photons à une fréquence qui ne coïncide pas avec la résonance»), et se transformer en muon et antimuon, ou quark et antiquark. Le quark inférieur et l'antiquark supérieur peuvent entrer en collision, s'annihiler à travers une particule W virtuelle et se transformer en un électron et un antineutrino. Ou deux gluons peuvent entrer en collision, s'annihiler à travers un gluon virtuel et se transformer en un quark supérieur et un antiquark supérieur (c'est le moyen le plus courant d'obtenir des quarks supérieurs sur un LHC).

2. Et si deux ondes dans les champs A et B ont des fréquences différentes, ν _A et ν _B ? Aux fréquences appropriées, les particules C peuvent encore apparaître, mais les conditions de résonance seront différentes et la particule C créée ne sera pas stationnaire. Voyons cela.

S'ils ont des fréquences différentes, alors deux quanta sans masse en collision auront

• Énergies diverses $$$E_A = h \ nu_A$ et $$$E_B = h \ nu_B$
• Différentes impulsions $$$p_A = + h \ nu_A / c$ et $$$p_B = - h \ nu_B / c$ (ici, plus signifie à droite, moins à gauche).

L'élan total p _A + p _{B est} désormais non nul. Mais l'élan persiste. Par conséquent, si la particule C peut se produire à la suite de l'annihilation des particules A et B, elle aura un élan p _C = p _A + p _B , donc elle se déplacera à gauche ou à droite, et ne restera pas immobile. Si ν _A > ν _B , alors il se déplacera vers la droite, sinon, vers la gauche.

Quelle quantité d'énergie est nécessaire pour créer une particule C en mouvement? Pour cela, plus d'énergie est nécessaire que pour une stationnaire - comme toute particule massive, son énergie et son élan doivent satisfaire

$$

$$E_C ^ 2 = (p_Cc) ^ 2 + (mc ^ 2) ^ 2$$

Ce qui signifie que E _C = mc ² si p _C = 0, ou plus si l'élan n'est pas nul. La loi de conservation de l'énergie et de l'élan nous dit que:

$$

$$E_C = E_A + E_B$$

$$

$$p_C = p_A + p_B = E_A / c - E_B / c$$

Où ai-je obtenu la dernière équation? Pour une particule sans masse, p = E / c, et pour nos particules en collision A et B, leurs impulsions sont opposées, de sorte qu'elles diffèrent par leur signe. Remplacez-le dans l'équation précédente et obtenez:

$$

$$(E_A + E_B) ^ 2 = (E_A - E_B) ^ 2 + (mc ^ 2) ^ 2$$

Les termes E _A ² et E _B ² sont mutuellement annihilés, et en déplaçant les termes E _A E _B vers la gauche, on obtient:

$$

En divisant par h ² et en utilisant la relation m = hν _min / c ² , on obtient la condition de résonance:

$$

$$(2 \ nu A) (2 \ nu B) = \ nu_ {min} ^ 2$$

Ce qui réduit correctement lorsque ν _A = ν _B à l'équation pour une particule immobile C, 2 ν = ν _min . Si cette condition n'est pas remplie, la particule C ne peut pas être créée. S'il est satisfait, c'est possible.

3. J'ai noté que de la même manière que l'équation du mouvement pour le champ C contient le terme AB, donc l'équation pour B contient le terme AC. Rappelez-vous ces équations:

$$

$$d ^ 2B / dt ^ 2 - c ^ 2 d ^ 2B / dx ^ 2 = y A C$$

$$

$$d ^ 2C / dt ^ 2 - c ^ 2 d ^ 2C / dx ^ 2 = (2 \ pi \ nu_ {min}) ^ 2 C + y A B$$

Ainsi, si la superposition des ondes A et B conduit à l'apparition d'une onde dans le champ C, la rendant non nulle, comme sur la Fig. 1, faut-il s'inquiéter du fait que cette nouvelle vague C chevauche la vague A existante et entraîne un changement dans le champ B? J'ai répondu "oui, mais nous pouvons négliger cela". Nous pouvons négliger pour une combinaison de deux raisons.

Tout d'abord, en raison du nombre "y" apparaissant avant les multiplications de AB et BC. L'impact sur le champ C du membre AB est proportionnel à y fois A multiplié par B. L'impact sur le champ B du membre AC est également proportionnel à y fois A multiplié par C, mais celui-ci sera à son tour égal à y ² fois A multiplié par par A multiplié par B. Donc, alors que y est inférieur à 1, y ² sera inférieur à y, donc l'effet sur B du membre AC est faible par rapport à l'effet sur C du membre AB - au moins pour les petites vagues A et B.En pratique, ces les ondes sont généralement petites: la particule A est un quantum de l'onde dans le champ A; par conséquent, l'onde A a de petites amplitudes d.

D'où la seconde raison, plus étrange mais plus convaincante: nous avons vu que si un quantum A rencontre un quantum B et se transforme en un quantum C, alors les ondes A et B disparaissent (s'annihilent). Après la création de C, il n'y a plus d'onde A, donc l'AC est nul, c'est-à-dire qu'il n'y a aucun effet sur le champ B.

Et le dernier hic: bien que je ne puisse pas le prouver sans calculs supplémentaires, même si les ondes A et B sont constituées d'un seul quantum, comme sur la Fig. 2, puis le processus de la Fig. 2 serait beaucoup plus compliqué si y était beaucoup plus grand que 1. Donc, la simplicité de l'histoire que j'ai racontée nécessite de petites valeurs de y. Dans la nature, la majorité des termes non linéaires en physique des particules sont généralement petits, donc ce que j'ai dit s'applique à la plupart des situations pratiquement applicables. Les exceptions sont très intéressantes - elles conduisent à la création d'objets complexes tels que les protons et autres hadrons.