
La physique est la science complexe la plus complexe; elle est tout aussi complexe, si fascinante. Si nous rejetons la composante mathématique, la physique devient immédiatement accessible à toute personne ayant de la curiosité et de l'imagination. Nous comprendrons facilement le concept de la théorie de la gravité, en évitant les équations mathématiques complexes. Par conséquent, à tous ceux qui pensent à ce qui rend les bleuets bleus et les fraises rouges; qui doute que le son se propage sous forme d'ondes; Quiconque se demande pourquoi le comportement de la lumière est si différent de tout autre phénomène dans l'univers, vous devez comprendre que tout cela est en physique quantique.
Ce livre présente (et démystifie) pour les gens ordinaires le monde magique de la science quantique, comme aucun autre livre. Elle parle des concepts scientifiques de base, des particules légères aux états de la matière et des causes de l'impact négatif des gaz à effet de serre, révélant chaque sujet sans utiliser de terminologie scientifique spécifique - des exemples de la vie quotidienne ordinaire. Bien sûr, un livre sur la physique quantique ne peut se passer d'un ensemble minimum de formules et d'équations, mais c'est un minimum nécessaire, compréhensible pour la plupart des lecteurs. Selon l'auteur, un livre vulgarisant la science devrait être accessible, mais pas au niveau du lecteur, mais pour élever et développer son intellect et son niveau culturel général.
Racquetball quantique et couleur des fruits
Une propriété clé des électrons liés aux atomes et aux molécules est que leurs états énergétiques sont discrets. Nous disons que l'énergie d'un électron peut être quantifiée, c'est-à-dire qu'un électron lié à un atome ou une molécule ne peut avoir que des valeurs énergétiques spécifiques. L'énergie change par étapes, et ces étapes ont certaines tailles discrètes. Les états énergétiques sont comme des escaliers. Vous pouvez vous tenir sur une étape ou passer à l'étape suivante, plus élevée. Cependant, il est impossible de rester à mi-chemin entre les deux étapes. Ces valeurs d'énergie discrètes ou quantifiées sont souvent appelées niveaux d'énergie. Contrairement aux escaliers ordinaires, les intervalles entre les niveaux d'énergie ne sont généralement pas les mêmes.
Un domaine important de la recherche quantique moderne est le calcul des états électroniques des molécules. Ce domaine est appelé chimie quantique. De tels calculs permettent d'obtenir des niveaux d'énergie quantifiés pour les électrons dans les molécules (niveaux d'énergie), ainsi que de calculer la structure des molécules. Le calcul de la structure de la molécule donne la distance entre les atomes et les positions de tous les atomes dans la molécule avec une précision limitée uniquement par le principe d'incertitude. Ainsi, les calculs de mécanique quantique permettent de déterminer la taille et la forme des molécules. Ces calculs sont importants pour comprendre les principes fondamentaux de la liaison des atomes aux molécules et pour la construction de nouvelles molécules. Avec le développement de la théorie quantique et l'émergence d'ordinateurs de plus en plus puissants et complexes capables de résoudre des problèmes mathématiques laborieux, de plus en plus de grosses molécules peuvent être étudiées en utilisant les méthodes de la chimie quantique. L'une des applications les plus importantes de la théorie quantique est le développement de produits pharmaceutiques. Les molécules peuvent être conçues de manière à avoir la taille désirée et à s'adapter à des loci spécifiques de protéines ou d'enzymes.
La chimie quantique nécessite des calculs très laborieux. Même pour l'atome d'hydrogène le plus simple, les calculs mécaniques quantiques sont mathématiquement très compliqués. Un atome d'hydrogène se compose d'un électron lié à un proton. Un proton, qui est le noyau d'un atome d'hydrogène, est une particule chargée positivement, et un électron est chargé négativement. L'attraction d'un électron chargé négativement vers un proton chargé positivement les maintient ensemble, maintenant l'atome d'hydrogène ensemble. Les détails du calcul des niveaux d'énergie de l'atome d'hydrogène ne seront pas présentés ici, mais dans les chapitres suivants, nous examinerons certaines caractéristiques des résultats de ces calculs. Ils donnent les niveaux d'énergie de l'atome d'hydrogène et ses fonctions d'onde. Ce sont les fonctions d'onde, c'est-à-dire les ondes d'amplitude de probabilité pour un atome d'hydrogène, qui sont le point de départ pour comprendre tous les atomes et toutes les molécules. Les atomes et les molécules sont complexes car ce sont des systèmes tridimensionnels absolument petits, et il est nécessaire de prendre en compte la façon dont les protons et les électrons interagissent entre eux.
Une particule dans une boîte - un cas classique
Il y a une tâche très simple liée à notre sujet. Il est connu comme le problème des particules dans une boîte. Il ne nécessite pas de mathématiques compliquées pour le résoudre, mais cette solution nous permet d'illustrer les propriétés importantes des électrons liés, par exemple, la quantification des niveaux d'énergie et la nature ondulatoire des électrons dans les états liés. Avant d'analyser la nature de l'électron dans une boîte unidimensionnelle de tailles atomiques, nous discutons du problème classique d'un terrain de jeu unidimensionnel idéal pour le racquetball afin d'identifier les différences entre les systèmes classique (grand) et mécanique quantique (absolument petit).
Dans la fig. 8.1 représente la «boîte» parfaite. Il est unidimensionnel. Ses murs sont considérés comme infiniment hauts, infiniment massifs et complètement impénétrables. Il n'y a pas d'air à l'intérieur de la boîte pour résister au mouvement. Sur la figure, l'intérieur de la boîte est désigné Q = 0, et l'extérieur - Q = ∞. Il a été dit plus tôt qu'une particule est appelée libre et qu'aucune force n'agit sur elle. Des forces surgissent lorsqu'une particule interagit avec quelque chose. Par exemple, une particule chargée négativement, comme un électron, peut interagir avec un proton chargé positivement. L'interaction sous forme d'attraction entre des particules de charges opposées va générer une force agissant sur l'électron. Lors du contrôle des électrons dans un tube cathodique (voir Fig. 7.3), un champ électrique génère une force agissant sur les électrons et les forçant à changer de direction.
Une mesure de l'interaction d'une particule avec quelque chose qui l'affecte, comme un champ électrique, s'appelle un potentiel et a la dimension de l'énergie. À l'avenir, le potentiel sera indiqué par la lettre Q. À l'intérieur de la boîte, Q = 0, comme dans le cas d'une particule libre. Cela signifie que la particule n'interagit avec rien à l'intérieur de la boîte. Il n'y a ni champs électriques ni résistance à l'air. Cependant, en dehors de la boîte, Q = ∞. Le potentiel infini signifie qu'une particule devrait avoir une énergie infinie pour être dans des zones en dehors de la boîte. L'expression Q = ∞ n'est qu'un moyen de formaliser l'affirmation que les parois de la boîte sont idéales. Une particule ne peut pas pénétrer à travers les murs ou sauter par-dessus, quelle que soit son énergie. Si vous placez une particule dans une telle boîte, elle ne peut pas glisser et restera toujours à l'intérieur. En ce sens, la particule est enfermée dans une boîte. Il peut être dans une région d'espace de longueur L, mais nulle part ailleurs.
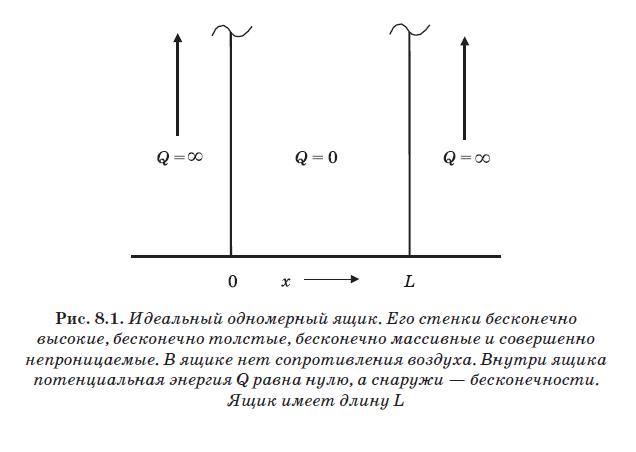
Dans la fig. La figure 8.2 montre une balle pour jouer au racquetball, rebondissant sur les murs d'un terrain de racquetball classique (grand) unidimensionnel idéal. Comme déjà mentionné, ces murs sont idéaux, mais il n'y a pas de résistance à l'air à l'intérieur. De plus, le ballon est également idéal, c'est-à-dire qu'il a une élasticité absolue. Lorsque la balle entre en collision avec le mur, elle se contracte comme un ressort et se redresse, la faisant rebondir. Les vraies balles ne sont pas parfaitement élastiques. Lorsque la balle est comprimée à l'impact, toute l'énergie dépensée pour la comprimer n'est pas repoussée du mur. Une partie de l'énergie dépensée pour comprimer la balle sert à la chauffer. Cependant, nous considérerons ici la balle parfaitement élastique. Lorsque vous frappez un mur, toute l'énergie cinétique de la balle, qui la fait se comprimer, est ensuite dépensée pour éloigner la balle du mur. Par conséquent, la vitesse de la balle juste avant la collision avec le mur est égale à la vitesse de son rebond après la collision.
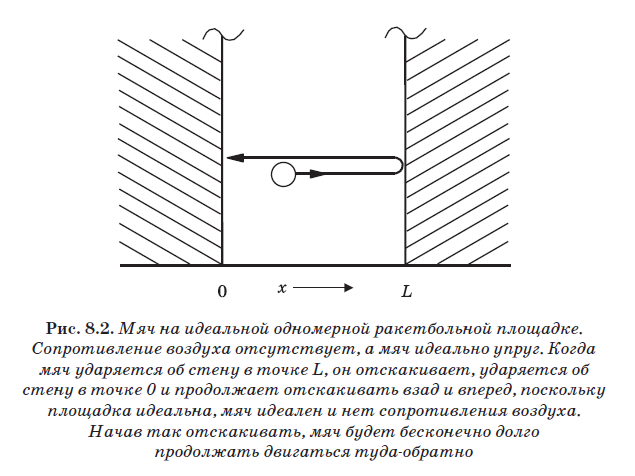
Sur ce terrain de racquetball idéal, la balle rebondit sur les murs sans aucune perte d'énergie; de plus, il n'y a ni résistance à l'air ni gravité. Par conséquent, la balle se déplacera toujours d'avant en arrière, se reflétant sur les murs. Il frappe le mur au point L, rebondit, entre en collision avec le mur au point 0, rebondit à nouveau et continue de se déplacer d'avant en arrière. À l'intérieur de la boîte, puisque le potentiel est nul (voir Fig. 8.1), aucune force n'agit sur la balle. Par conséquent, son énergie est purement cinétique:
où m est la masse de la balle et V est sa vitesse. Si la balle subit de faibles influences externes, sa vitesse deviendra légèrement inférieure et la valeur Ek diminuera également légèrement. Dans ce racquetball idéal, l'énergie peut changer en permanence. La valeur d'Ek peut augmenter ou diminuer arbitrairement en fonction uniquement de la force de l'impact sur le ballon.
Une autre caractéristique importante du racquetball classique est la possibilité d'arrêter le ballon afin qu'il repose immobile sur le sol. Dans cette situation, sa vitesse est nulle: V = 0. Et puisque V = 0, alors Ek = 0. À V = 0, l'impulsion est également nulle, car p = mV, donc nous connaissons exactement l'impulsion. Si la balle repose sur le sol (V = 0), alors sa position est connue. Si nous notons cette position x (voir Fig. 8.2), alors la valeur de x sera dans la plage de 0 à L. La valeur de x ne peut pas prendre d'autres valeurs, puisque la balle est sur le terrain (dans la boîte) et ne peut pas être à l'extérieur de pour des murs parfaits. La balle peut être placée dans une position spécifique x sur le sol du terrain, puis sa position sera connue avec certitude. C'est une propriété d'un terrain de jeu macroscopique, même idéal. C'est un système classique, et on peut y connaître précisément et simultanément l'élan p et la position x.
Le terrain de racquetball a une longueur de 12 m, le diamètre de la balle est de 5,6 cm et son poids est d'environ 0,04 kg. De toute évidence, le jeu de racquetball est décrit par la mécanique classique. Avec l'aide de la lumière, vous pouvez suivre le rebond de la balle d'avant en arrière sans les affecter.
Particule dans une boîte - boîtier quantique
Qu'est-ce qui changera si nous nous tournons maintenant vers la considération du racquetball quantique? Le site reste idéal, mais maintenant sa longueur n'est plus de 12 m, mais 1 nm (10–9 m). De plus, la particule a une masse électronique de 9,1 10–31 kg et non de 0,04 kg. C'est donc le problème d'une particule quantique dans une boîte.
Nous pouvons immédiatement dire que la plus petite énergie d'une particule quantique dans une boîte de taille nanométrique ne peut pas être nulle. Sur un terrain de racquetball classique, la vitesse de balle V est possible, qui est égale à zéro, ce qui signifie que l'impulsion p = mV peut également être nulle. De plus, la position de la balle x a une signification clairement définie. Par exemple, la balle peut rester immobile (V = 0) exactement au milieu du terrain, ce qui correspond à x = L / 2. Dans ce cas, pour notre racquetball classique, ∆p = 0 et ∆x = 0. La valeur du produit ∆x∆p = 0 ne correspond pas au principe d'incertitude de Heisenberg, ce qui est normal, puisque nous parlons du système classique. Cependant, une particule absolument petite dans une boîte de taille nanométrique est un objet quantique et doit obéir au principe d'incertitude, qui stipule que ∆x∆p ≥ h / 4. Si V = 0 et x = L / 2, alors nous connaissons à la fois x et p, ce qui signifie que ∆x∆p = 0, comme dans le racquetball classique. Pour un système quantique, ce n'est pas possible. Ainsi, V ne peut pas être égal à zéro. Une particule ne peut pas rester immobile à un point donné. Et si la valeur de V est non nulle, alors la valeur de Ek ne peut pas être égale à zéro. Le principe d'incertitude dit que la plus petite énergie de notre racquetball quantique ne peut pas être nulle. Une boule quantique ne reste jamais immobile.
Valeurs d'énergie des particules quantiques dans une boîte
Quelle énergie une particule quantique peut-elle avoir dans une boîte de taille nanométrique? Cette question peut être répondue sans calculs compliqués, mais nous devons d'abord revenir aux vagues. Au chapitre 6, nous avons parlé des fonctions d'onde des particules libres. La fonction d'onde d'une particule libre avec une impulsion spécifique p est une onde qui s'étend dans tout l'espace. Ainsi, un électron avec une impulsion parfaitement définie est une onde délocalisée, couvrant tout l'espace. La probabilité de détecter un électron libre est la même partout. Un tel électron a une énergie cinétique bien définie Ek = 1 / 2mV2, car il a une impulsion bien définie p = mV.
L'électron dans la boîte nanométrique est similaire à notre particule libre en ce qui concerne la région intérieure de la boîte, où Q = 0. Il n'y a pas de potentiel à l'intérieur de la boîte, et donc il n'y a pas de forces agissant sur la particule. À cet égard, elle est très similaire à une particule libre, sur laquelle aucune force n'agit non plus. Cependant, il existe une différence importante entre la particule dans la boîte et la particule libre - ce sont les parois de la boîte. L'électron dans la boîte n'est qu'à l'intérieur de la boîte. La nature idéale de la boîte ne permet pas à sa fonction d'onde de se propager à tout l'espace. La particule est à l'intérieur de la boîte et ne peut jamais être à l'extérieur. La fonction d'onde définit l'amplitude de la probabilité de détecter une particule dans une certaine région de l'espace. Il s'agit d'une interprétation de Born de la fonction d'onde. Si notre électron ne peut être détecté qu'à l'intérieur de la boîte et jamais à l'extérieur, alors la probabilité de sa détection dans la boîte devrait être finie et à l'extérieur - zéro. Si la probabilité de trouver une particule en dehors de la boîte est nulle, alors la fonction d'onde doit être nulle à tous les points en dehors de la boîte.
Ainsi, nous sommes arrivés à la conclusion que la fonction d'onde d'une particule dans une boîte est similaire à la fonction d'onde d'une particule libre, mais la fonction d'onde doit être nulle en dehors de la boîte. Dans son interprétation de la nature de la fonction d'onde quantique-mécanique, Born a imposé des restrictions physiques sur la forme que peut prendre la fonction d'onde. L'un d'eux est qu'une bonne fonction d'onde doit être continue. Cette condition signifie que la fonction d'onde doit changer en douceur d'un endroit à l'autre. Un changement de position infiniment petit ne peut pas conduire à un saut inattendu de probabilité. C'est une pensée très simple. Si la probabilité de détecter une particule dans une très petite région de l'espace est, par exemple, de 1%, alors un décalage d'une quantité incroyablement faible ne peut pas rendre soudain la probabilité de détecter une particule égale à 50%. Cela ressort clairement des images des paquets d'ondes de la Fig. 6.7. La probabilité varie en douceur d'un endroit à l'autre. Cela nous permet d'ajouter quelque chose à la description des fonctions d'onde d'une particule dans une boîte, en plus du fait que ce sont des ondes d'amplitudes finies à l'intérieur de la boîte et d'amplitude nulle à l'extérieur. Étant donné que la fonction d'onde doit être continue, elle doit avoir une amplitude nulle directement sur la paroi du boîtier de l'intérieur pour coïncider avec l'amplitude nulle de la fonction d'onde à l'extérieur du boîtier.
Dans la fig. La figure 8.3 montre la discontinuité (interdite) de la fonction d'onde à l'intérieur du boîtier. La fonction d'onde est indiquée (lettre grecque "fi"). L'axe vertical représente l'amplitude de la fonction d'onde. La ligne pointillée indique son niveau zéro. Les fonctions d'onde, qui sont des ondes d'amplitude de probabilité, peuvent osciller entre des valeurs positives et négatives. La fonction d'onde illustrée à la Fig. 8.3, a près des parois des valeurs autres que 0. Cependant, la fonction d'onde doit être nulle en dehors de la boîte, c'est-à-dire que pour des valeurs de x inférieures à 0 et supérieures à L, elle doit être nulle. Dans la figure, la fonction d'onde passe de façon inattendue d'une valeur non nulle près du mur à l'intérieur de la boîte à une valeur zéro immédiatement derrière le mur à l'extérieur de la boîte. Ainsi, la fonction d'onde représentée sur la Fig. 8.3 n'est pas valide car il n'est pas continu. Cette fonction ne peut pas représenter une particule quantique dans une boîte.
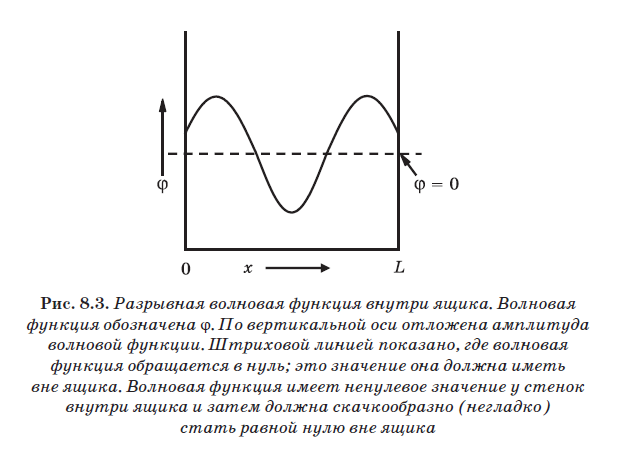
La fonction d'onde doit avoir une valeur nulle aux murs
Pour que les fonctions d'onde représentant la particule dans la boîte soient physiquement acceptables, leurs valeurs sur les murs doivent être nulles, puis elles ne subiront pas d'écart sur les murs. Il n'est pas difficile de remplir cette condition. La fonction d'onde oscille entre des valeurs positives et négatives. Chaque fois, passant de valeurs positives à négatives ou de négatives à positives, il passe par zéro. En fait, les points zéro sont séparés les uns des autres par la moitié de la longueur d'onde. Par conséquent, pour obtenir de bonnes fonctions d'onde d'une particule dans une boîte, nous devons choisir des ondes dont la longueur permet de les empiler dans la boîte de sorte que les points zéro soient situés exactement sur les murs.
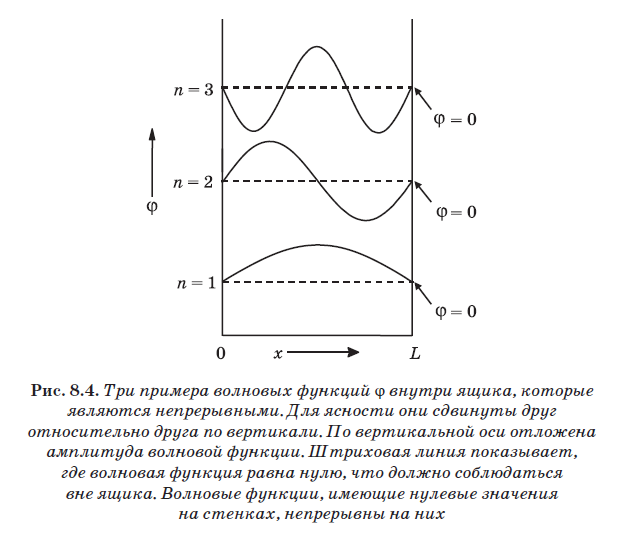
Dans la fig. 8.4 montre trois exemples d'ondes qui conviennent au rôle des fonctions d'onde pour une particule dans une boîte. Le plus bas d'entre eux est désigné n = 1 et se compose d'une demi-onde. Elle part à gauche à l'amplitude 0, passe le maximum puis retombe à zéro sur la paroi au point L. L'onde suivante, située au dessus et marquée n = 2, consiste en une oscillation complète. Il commence également à la paroi gauche à l'amplitude 0, passe un pic positif, revient à zéro, puis un pic négatif suit et revient à zéro sur la paroi au point L. L'onde indiquée par n = 3 contient une demi-période. Toute onde contenant un nombre entier de demi-ondes, c'est-à-dire 1, 2, 3, 4, 5, etc., la moitié de la longueur d'onde et située de telle sorte qu'elle commence à zéro à gauche et se termine à zéro à droite, convient.
La valeur n est le nombre de demi-ondes d'une fonction d'onde particulière. Pour n = 1, la longueur d'onde est 2L, car la longueur de la boîte est L, et n = 1 correspond à la moitié de la longueur d'onde. Pour n = 2, la longueur d'onde est L, car exactement une longueur d'onde est placée entre les parois. Pour n = 3, trois demi-ondes sont placées entre les murs, soit 1,5 = L. Dans ce cas = L / 1,5, soit = 2L / 3. Notez qu'une règle générale se trouve ici: = 2L / n, où n est un entier. Pour n = 1, nous obtenons = 2L, pour n = 2 - = 2L / 2, pour n = 3 - = 2L / 3, etc.
»Plus d'informations sur le livre sont disponibles sur
le site Web de l'éditeur»
Contenu»
ExtraitPour les lecteurs de ce blog, une remise de 20% sur le coupon -
Fire