🤜🏻 👨🏻‍⚕️ 🦓 Comment fonctionne le champ Higgs: 2) pourquoi le champ Higgs est-il en moyenne non nul ⛹🏼 📱 🤟🏻

Comment fonctionne le champ Higgs:

Comment se fait-il que le champ de Higgs dans la nature n'ait pas une valeur moyenne de zéro, alors que d'autres champs de la nature (apparemment élémentaires) que nous connaissons ont zéro? [Très petits caractères: d'autres champs, à l'exception du champ gravitationnel du niveau le plus bas, sont appelés métriques, cela vous permet de déterminer l'existence de l'espace et du temps].

Premièrement, les champs de fermions ne peuvent pas avoir une grande valeur constante non nulle dans la nature. Cela est dû à la différence entre les fermions et les bosons. Les bosons peuvent être en moyenne non nuls, mais pas les fermions. Vous pouvez donc oublier les électrons (et leurs cousins muons et tau), les neutrinos et les quarks. Petits caractères: les fermions peuvent s'apparier entre eux ou avec des antifermions et créer des bosons composites, qui peuvent être en moyenne non nuls. C'est le cas pour les quarks supérieurs et inférieurs et leurs antiquarks, et pour les électrons dans un supraconducteur. Mais c'est une longue histoire, et elle ne concerne pas directement la nôtre.

Qu'en est-il des domaines des photons, des gluons, du W et du Z? Ce sont tous des bosons. En principe, ces champs pourraient avoir une valeur moyenne non nulle constante sur l'Univers. Mais les expériences, pas la théorie, disent que ce n'est pas le cas. Une valeur non nulle suffisamment grande du champ électrique conduirait à l'apparition de divers effets, que nous n'observons pas. Le plus important d'entre eux serait une violation de l'invariance rotationnelle à grande échelle. Un champ électrique est un vecteur (spin-1), il indique dans une certaine direction, donc s'il n'est pas nul, alors la direction dans laquelle cette valeur indique doit être différente de toutes les autres. (Fig.1, en bas à gauche).

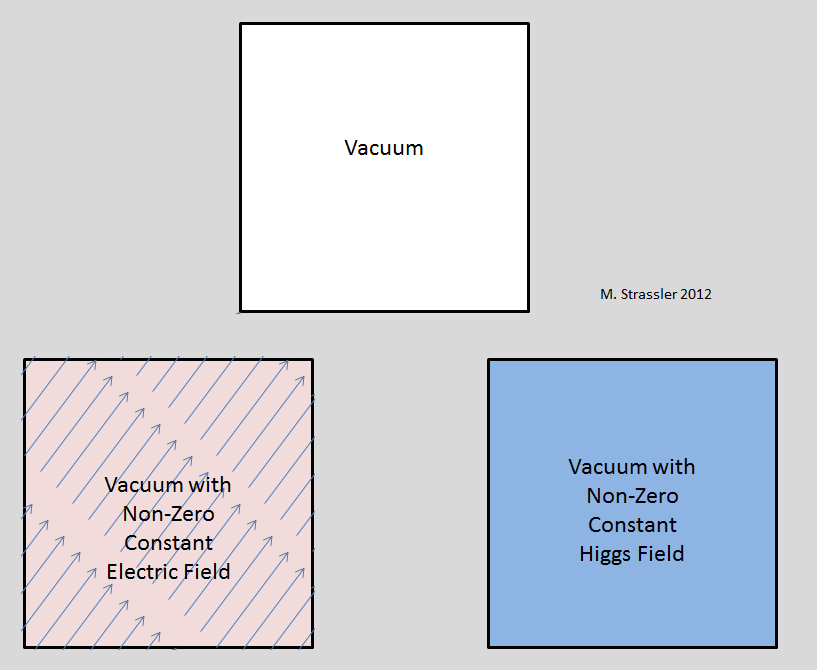Fig. 1

Le champ de Higgs est scalaire (spin-0), il n'indique nulle part. Parmi d'autres champs scalaires (ni élémentaires ni relativistes), nous pouvons donner des exemples du champ de densité de l'air, du champ de pression à l'intérieur de la Terre et de la température de l'océan. En tout point de l'espace et du temps, la densité ou la pression ou la température n'est qu'un nombre, et le champ électrique est un nombre et une direction. Donc, si le champ de Higgs a une valeur différente de zéro, aucune direction préférée n'apparaît - Fig. 1, en bas à droite. Ce qui est plus étrange (car il est relativiste), le champ de Higgs ne génère aucun cadre de référence préféré. Pour la densité de l'air, il existe un système de référence préféré, car vous vous reposez par rapport à l'air ou vous vous y déplacez. Mais pour le champ de Higgs, ce n'est pas le cas; tous les observateurs se reposent par rapport à lui. Par conséquent, le succès de l'Einstein SRT, qui décrit toutes sortes de phénomènes, f contredit la présence d'un champ scalaire relativiste de valeur non nulle, tel que le champ de Higgs. En bref, en présence d'un champ de Higgs non nul, le vide se comporte exactement comme il se comporterait à H = 0; sa présence ne peut être détectée que par l'effet sur la masse des particules (ou par quelque chose de plus dramatique, par exemple, l'utilisation du LHC pour créer des particules de Higgs).

Le moyen le plus simple pour le champ de Higgs serait de maintenir une valeur non nulle dans tout l'univers s'il avait une valeur d'équilibre non nulle H ₀ impliquée dans son équation de mouvement de classe 1:

d^{2} H / d t^{2} - c^{2} d^{2} H / d x^{2} = - (2 p i n u_{m i n})^{2} (H - H_{0})

$d ^ 2H / dt ^ 2 - c ^ 2 d ^ 2H / dx ^ 2 = - (2 \ pi \ nu_ {min}) ^ 2 (H - H_0)$

(Ce devrait être la classe 1, pas la classe 0, pour des raisons qui deviendront claires pour nous après avoir discuté de la particule de Higgs). En fait, la situation est un peu plus compliquée. L'équation correcte ressemblerait à ceci:

d^{2} H / d t^{2} - c^{2} d^{2} H / d x^{2} = a^{2} H - b^{2} H^{3}

$d ^ 2H / dt ^ 2 - c ^ 2 d ^ 2H / dx ^ 2 = a ^ 2 H - b ^ 2 H ^ 3$

Où a et b sont des constantes (leurs carrés sont positifs! Notez le signe plus devant un ² H, et comparez-le avec le moins dans l'équation précédente), dont nous parlerons plus tard. Cela peut être réécrit comme:

d^{2} H / d t^{2} - c^{2} d^{2} H / d x^{2} = - b^{2} H (H^{2} - [a / b]^{2})

$d ^ 2H / dt ^ 2 - c ^ 2 d ^ 2H / dx ^ 2 = - b ^ 2 H (H ^ 2 - [a / b] ^ 2)$

Si H (x, t) est une constante dans l'espace et le temps, alors dH / dt = dH / dx = 0, donc

0 = - b 2 H (H 2 - [a / b]^{2})

$0 = - b2 H (H2 - [a / b] ^ 2)$

(quand H (x, t) est une constante en x et t), et il a des solutions (pour l'instant, nous allons tout simplifier grandement):

1. H = 0
2. H = + a / b
3. H = - a / b

En d'autres termes, les positions d'équilibre sont trois, pas une. Petits caractères: je simplifie grandement ici, mais sans préjudice du sens.

Ce n'est pas immédiatement clair, mais la solution H = 0 est instable. La situation est similaire à l'équation du mouvement d'une balle dans un bol de la forme représentée sur la Fig. 2 - similaire au fond d'une bouteille de vin. Il a également trois positions d'équilibre, une à 0 et deux à ± x ₀ . Mais évidemment, la position à 0 est instable - toute poussée fera rouler la balle rouge loin de x = 0, un changement cardinal de la situation. Inversement, l'équilibre à x = x _{0 est} stable, car toute poussée fera osciller la balle verte avec une petite amplitude autour du point x = x ₀ - pas un changement aussi radical. Il en sera de même pour une boule vert clair à x = -x ₀ . De même, bien que H = 0 soit la solution à l'équation pour le champ de Higgs, l'histoire de notre univers s'est avérée suffisamment compliquée pour garantir que le champ de Higgs devrait être correctement lancé, de sorte qu'il ne pourrait pas rester dans cette position. Au lieu de cela, le champ Higgs était dans une solution avec une valeur non nulle et dans une situation stable.

Pendant des décennies, grâce à une combinaison d'expériences et de théorie, nous savions que la valeur du champ de Higgs (qui est traditionnellement appelé "v") est de 246 GeV. Cela nous donne une idée de ces constantes a et b:

a = vb = (246 GeV) b

Ainsi, nous pouvons déterminer de a à b, et nous pouvons réécrire l'équation de mouvement de Higgs:

d^{2} H / d t^{2} - c^{2} d^{2} H / d x^{2} = - b^{2} H (H^{2} - v^{2})

$d ^ 2H / dt ^ 2 - c ^ 2 d ^ 2H / dx ^ 2 = - b ^ 2 H (H ^ 2 - v ^ 2)$

Mais cela ne nous donne pas une idée de b lui-même. Dans le prochain article, nous en apprendrons plus sur lui.

Maintenant, bien que j'aie tout préparé pour que H puisse être égal à v ou –v, peu importe que le champ de Higgs soit positif ou négatif (en fait, il y a encore plus de possibilités, voir ci-dessous); le monde sera exactement le même, avec la même physique, car rien ne dépend du signe de H. Cela ne devient pas évident tout de suite, mais ça l'est; un indice - où que vous trouviez H dans les équations que je décris ou dans la description du fonctionnement du champ de Higgs, H ² apparaît partout, et pas seulement H - et H ² ne dépend pas de H = v ou H = -v . [Petits caractères: en fait, H est un champ complexe, avec les parties réelles et imaginaires, donc H peut être égal à v fois tout nombre complexe z pour lequel | z | = 1; et en fait, H * H = | H | ² , mais cela ne dépend pas de z. Et même ce n'est pas tout! Mais assez pour aujourd'hui.]

Si vous trouvez un moyen (par exemple, en entrant en collision des protons les uns avec les autres au Grand collisionneur de hadrons) pour en quelque sorte pousser ou introduire une perturbation dans le champ de Higgs, il oscillera de long en large - c'est-à-dire que des ondes y apparaîtront sous la forme

H = v + A c o s [2 p i (n u t - x / l a m b d a)]

$H = v + A cos [2 \ pi (\ nu t - x / \ lambda)]$

Où A est l'amplitude des ondes, ν et λ sont la fréquence et la longueur d'onde, et la relation entre ν et λ dépend de la forme exacte de l'équation du mouvement, en particulier, de b et v. Puisque le champ de Higgs est quantique, l'amplitude de ces ondes sera quantifiée et le quantum de ces ondes est ce que nous appelons la particule de Higgs. La prochaine fois, nous examinerons les propriétés de ces particules.

Comment fonctionne le champ Higgs: 2) pourquoi le champ Higgs est-il en moyenne non nul

More articles: