Bonjour, je m'appelle Alexander et je suis physicien. De l'extérieur, cela peut sembler être un verdict, mais en fait c'est le cas. Il s'est avéré que je fais de la recherche fondamentale en physique, à savoir étudier les particules chargées accélérées: les protons et tous ces plus gros sont des ions positifs, c'est-à-dire. Dans les études, je n'utilise pas de gros accélérateurs comme les LHC, mais je tire sur la feuille avec un laser, et un élan de proton s'envole hors de la feuille.

Maintenant, quelques mots sur moi. Je suis diplômé de la faculté de photonique et d'opto-informatique de l'ITMO à Saint-Pétersbourg, puis je suis allé dans une magistrature à l'Université Aalto (en Finlande) dans le domaine des micro et nanotechnologies, puis j'ai craché sur toutes ces petites choses, des microscopes, et surtout sur une salle blanche. Et je suis entré dans la science fondamentale avec de grands lasers. Maintenant, je travaille dans une école doctorale dans le sud-ouest de la Suède dans la ville de Lund à l'université du même nom. Il s'agit de la distance d'un coup de canon de Copenhague.

Comme accéléré, donc volé

Les accélérateurs de particules chargées eux-mêmes ne sont pas une idée nouvelle, mais la méthode par laquelle je les accélère est relativement fraîche, à peu près du même âge que moi. Il vous permet de réduire considérablement la taille de l'accélérateur et son coût, y compris le coût des travaux et de la maintenance. La différence entre les deux types peut être estimée dans l'image ci-dessous.

À gauche, un accélérateur linéaire électrostatique (légèrement démonté); À droite, mon petit mais fier fabricant de trous

Comparons plus en détail ces deux modèles de génie physique sombre. Regardez l'accélérateur gauche et la droite, puis encore à gauche et encore à droite: oui, le mien est sur un cheval (une blague - commentaire de l'auteur). En fait, le mien ne prend qu'un mètre de diamètre et les protons eux-mêmes sont accélérés à partir d'un morceau de papier d'aluminium. Son support est situé exactement au milieu du cercle, portant une belle jupe en cuivre. Il est beaucoup plus simple et plus compact que l'échantillon de gauche, qui est de la taille d'un bus et en plus est rempli de gaz asphyxiant. Ainsi, s'étant imposé en abondance (il arrive souvent en physique que plus c'est petit, mieux c'est), on peut se tourner vers la physique du processus d'accélération.

Puisque nous accélérons les particules chargées, il est plus logique de le faire avec un champ électrique. Le champ que nous caractériserons par la tension. Pour ceux qui sont allés à l'avant et à l'arrière après l'école, permettez-moi de vous rappeler: la force du champ électrique est une grandeur physique vectorielle caractérisant le champ électrique à un point donné et numériquement égale au rapport de la force agissant sur une charge à point fixe placée à un point donné du champ, l'ampleur de cette charge (copier-coller sale de Wikipedia). Il a une dimension de V / m. Pour revenir à la comparaison, l'accélérateur de gauche accélère les protons à 4 MeV (mégaélectron-volts), soit 2,77 * 10 ⁷ m / s ou 9,2% de la vitesse de la lumière. Étant donné que la charge de protons est de 1 et que la longueur de l'accélérateur est de deux mètres, l'intensité du champ sera de 2 MV / m. Ici, nous avons supposé que, dans tous les endroits, le champ est dirigé dans une seule direction et, en général, était très proche de la vérité. Un accélérateur élégant a une intensité de champ de l'ordre de plusieurs TV / m, soit environ un million de fois plus. Pourtant, il convient de reconnaître que sa longueur n'est que de quelques microns.

Donc, à ce stade, nous avons découvert dont le champ est plus raide. Il est temps de se tourner vers les mécanismes physiques et d'ingénierie que ce champ crée. Dans le cas d'un accélérateur classique, il y a deux tôles, dont l'une est chargée négativement, et la seconde en aucune façon. Rappelez-vous l'expérience de l'école sur le frottement d'un bâton en ébonite avec un morceau de laine. Ici, le principe est exactement le même, mais l'exécution est beaucoup plus compliquée. Si vous accélérez les protons de la feuille, le champ est créé par des électrons, les électrons sortent du plasma chaud, le plasma est obtenu et chauffé par un laser, et tout cela est le reste du poste.

Voulez-vous que je le frappe, et il devient violet en un grain?

Si vous frappez assez fort, vous pouvez voir de nombreux phénomènes physiques merveilleux. C'est ainsi que les gars de Harvard ont obtenu de l'hydrogène métallique, puis l'ont perdu.

Dans mon cas, je tire la feuille avec un laser. Je le décrirai plus en détail après avoir expliqué la physique non triviale des processus d'obtention de la matière dense chaude, qui est exactement le nom du plasma en termes scientifiques, qui est responsable du triomphe de l'accélération de mes protons. Et maintenant, tout d'abord.

Le laser génère des impulsions d'une longueur d'onde de 800 nm et de 35 fs pendant une durée (10 ^-15 s), c'est-à-dire que la longueur d'impulsion réelle dans le vide est d'environ 10 μm. Environ 2 J d'énergie sont poussés dans cette impulsion, et c'est beaucoup. Si nous prenons cette impulsion et la concentrons sur une feuille dans un spot rond soigné de 5 microns de diamètre, alors l'intensité sera de l'ordre de 10 ²⁰ W / cm ² . C'est indécent beaucoup. Encore une petite comparaison: l'acier peut être facilement coupé à une intensité de 10 ⁸ W / cm ² (environ).

En fait, en raison des caractéristiques de conception de l'amplificateur, l'impulsion laser a un piédestal précédent d'une durée d'environ 500 ps, et ce piédestal aide grandement à bien accélérer les protons.

Ionisé - signifie armé

Rappelez-vous ce qui arrive à la lumière lorsqu'elle pénètre dans une substance. L'énergie doit être conservée, ce qui signifie qu'il n'y a que trois variantes d'événements: la réflexion, la transmission et l'absorption. Dans la vie difficile, tout cela est répertorié à la fois. Au tout début, nous nous intéressons à l'absorption.

Nous avons donc un piédestal, sur lequel nous nous concentrons également parfaitement sur un morceau de papier d'aluminium, et il y est parfaitement absorbé. Afin de ne pas entrer dans la complexité de la physique du solide, nous considérons l'absorption d'un atome autonome. De la mécanique quantique, nous savons que seul un photon peut être absorbé, dont l'énergie est exactement égale à l'énergie de la transition d'un électron d'un état à un autre. Si l'énergie des photons est supérieure à l'énergie d'ionisation (c'est-à-dire l'envoi d'un électron du nid du parent à un voyage libre), alors l'excès ira dans l'énergie cinétique de l'électron, tout est simple. Dans notre cas, les photons d'une longueur d'onde de 800 nm n'ont pas assez d'énergie (c'est l'énergie d'un photon, pas toute l'impulsion!) Pour ioniser la cible, mais ici la physique vient à notre secours. Rappelez-vous, j'ai mentionné une plus grande intensité de rayonnement? Si, en annexe, on se souvient encore que la lumière peut être représentée comme un flux de photons, et que l'intensité y est directement proportionnelle, alors il s'avère que le flux de photons est très important. Et si le flux est si important, il est probable que plusieurs photons arriveront au même endroit et en même temps, et lorsque leur énergie sera absorbée, ils s'accumuleront et l'ionisation se produira toujours. Curieusement, ce phénomène est appelé ionisation multiphotonique, et nous l'utilisons régulièrement.

Pour le moment, nous savons que les électrons ont été arrachés avec succès, ce qui signifie que l'impulsion principale arrive au plasma fini et commence à le réchauffer.

Fondamentaux de la physique des plasmas (pas de blague, ah)

Avant de chauffer, il vaut la peine de parler du plasma en tant qu'état de la matière. Le plasma, c'est comme un gaz, seuls les électrons sont séparés et les noyaux sont séparés. Nous considérerons notre plasma comme un gaz presque idéal, mais composé d'électrons.

Notre principale caractéristique d'un plasma sera sa densité (le nombre d'électrons par unité de volume), cette valeur sera notée $ n_e $ (à ne pas confondre avec l'indice de réfraction!), Et la température de ces mêmes électrons, c'est-à-dire leur vitesse moyenne. Ceci est décrit par la distribution de Boltzmann de la même manière que dans le cours de physique scolaire:

$$ afficher $$ \ frac {m_e v ^ 2} {2} = \ frac {1} {2} k_B T_e, $$ afficher $$

où suit facilement

$$ afficher $$ \ langle v \ rangle = \ sqrt [] {k_B T_e / m_e}, $$ afficher $$

où

$ inline $ k_B $ inline $ - Constante de Boltzmann

$ inline $ T_e $ inline $ Est la température électronique, et

$ inline $ m_e $ inline $ Est la masse de l'électron. Oui, nous avons considéré ici un cas unidimensionnel, mais nous n'avons vraiment pas besoin de plus pour décrire nos processus, en fait.

Maintenant, nous appliquons un champ électrique au plasma déjà décrit. Permettez-moi de vous rappeler que le plasma est composé de particules chargées, ce qui signifie qu'à une densité donnée à une certaine distance de l'endroit où nous avons appliqué le champ, les électrons obscurciront (protégeront) la source (une telle foule de petits Matrosov - note de l'auteur). La distance nécessaire pour cela s'appelle la longueur de Debye et est donnée par l'équation

$$ affiche $$ \ lambda_D = \ sqrt [] {\ frac {\ epsilon_0 k_B T_e} {q ^ 2_e n_e}}. $$ afficher $$

Ici

$ inline $ q_e $ inline $ évidemment la charge d'un électron, et

$ inline $ \ epsilon_0 $ inline $ - constante diélectrique du vide, telle constante fondamentale. Nous analysons un peu cette formule pour voir la physique simple du processus. En augmentant la densité des électrons, nous réduisons la distance moyenne entre eux, par conséquent, pour une distance plus petite, nous collectons suffisamment d'électrons pour protéger complètement notre champ. En revanche, plus la température est élevée, plus la distance moyenne entre les électrons est grande.

En raison de l'effet d'écran et d'une température moyenne bien définie des électrons (selon la température), le plasma ne réagit pas instantanément à un champ arrivant soudainement. Il est logique de supposer que le temps de réponse est lié à la longueur de Debye et à la vitesse des électrons. Une bonne analogie est de jeter une pierre sur un lac. Comparée à un lac entier, la pierre agit à la surface de l'eau de façon ponctuelle. Une partie de l'eau change immédiatement (c'est là qu'elle s'est effondrée), puis les vagues commencent à se propager à la surface de l'eau. Dans le cas du plasma, un champ électrique apparaissant soudainement est une pierre. La taille du panache est déterminée par la longueur de l'écran (le champ n'agit pas au-delà) et la propagation des ondes dépend de la proximité des électrons. Nous pouvons introduire une caractéristique telle que le temps de réponse plasma:

$ inline $ t_D = \ lambda_D / v $ inline $ . Dans l'ensemble, il nous montre le temps pendant lequel les informations sur un changement dans le champ appliqué atteindront les électrons qui, pour ainsi dire, ne l'ont pas vu.

Puisque nous sommes physiciens, nous n'aimons pas vraiment le temps. Il est beaucoup plus pratique de travailler avec des fréquences, nous introduisons donc le concept de la fréquence naturelle d'un plasma. Cette valeur nous montrera combien de fois nous pouvons changer le champ afin que toute l'accumulation d'électrons, que nous appelons fièrement le plasma, ait le temps de répondre à ces changements. Eh bien, quoi de plus simple? Divisez l'unité par le temps de réponse, et voici - la fréquence:

$$ affiche $$ \ omega_p = \ frac {1} {t_D} = \ sqrt [] {\ frac {q ^ 2_e n_e} {\ epsilon_0 m_e}}. $$ afficher $$

Il est facile de voir que la fréquence propre des oscillations du plasma dépend de la densité électronique. Plus il y a d'électrons, plus la fréquence est élevée. Vous pouvez tirer une autre analogie, mais cette fois avec un pendule à ressort. La haute densité électronique nous indique qu'ils sont plus proches les uns des autres, ce qui signifie qu'ils interagissent plus fortement. Nous supposons que leur interaction en proportion directe est associée à l'élasticité du ressort du pendule. Et plus l'élasticité est élevée, plus la fréquence d'oscillation est élevée.

La fréquence naturelle d'un plasma détermine également son indice de réfraction. Pour être honnête, nous écrivons l'équation d'onde du mouvement collectif des électrons dans un plasma, puis supposons de petits changements dans la densité électronique (nous ne le ferons pas ici car c'est ennuyeux), puis nous définissons l'indice de réfraction comme suit:

$$ affiche $$ \ eta = \ sqrt [] {1- \ frac {\ omega ^ 2_p} {\ omega ^ 2_0}}. $$ afficher $$

Ici

$ inline $ \ omega_0 $ inline $ Est la fréquence circulaire du champ électrique appliqué. Elle est en rad / s et non en Hz!

Nous regardons attentivement cette expression. En tant que physicien expérimental, je ne bois pas les âmes en nombre réel, mais j'essaie d'ignorer les âmes complexes, en particulier l'indice de réfraction complexe. Eh bien, comment la lumière peut-elle finalement se propager dans la matière i fois plus lentement que dans le vide? C'est une sorte de non-sens! Pas vraiment, mais plus à ce sujet une autre fois. Si

$ inline $ \ omega_0> \ omega_p $ inline $ , alors l'expression a un sens réel, et un champ électrique alternatif se propage à l'intérieur de notre plasma. Tout le monde est content, et nous appellerons un tel plasma insuffisamment dense. Cependant, si

$ inline $ \ omega_0 <\ omega_p $ inline $ , alors l'indice de réfraction devient non seulement complexe, mais entièrement imaginaire. Dans ce cas (et pas seulement parce que je le voulais), l'onde ne s'y propage pas du tout, mais se reflète immédiatement sans perte. C'est un plasma trop dense. Un phénomène très cool, au fait. Il s'agit d'un miroir à plasma.

Et en dessert

$ inline $ \ omega_0 = \ omega_p $ inline $ . Il s'agit d'un plasma de densité critique. Dans ce cas, il commence à entrer en résonance avec un champ électrique alternatif de forçage (fourni par nos soins). Pour un tel cas spécial, vous pouvez même introduire le concept de densité critique et le définir comme ceci:

$$ affiche $$ n_c = \ frac {\ epsilon_0 m_e \ omega ^ 2_0} {q ^ 2_e}. $$ afficher $$

Naturellement, la densité critique est différente pour chaque fréquence du champ de forçage.

CHOC! Chauffage au plasma! Pour ce faire, seulement ...

Dans notre cas, nous nous concentrerons sur un seul mécanisme de chauffage, qui prévaut dans l'expérience.

Pour commencer, laissez le plasma que nous avons formé par le piédestal avoir un gradient de densité lisse, dans ce cas, nous avons un chauffage par absorption par résonance. Une illustration de cela dans l'image ci-dessous.

Illustration du processus d'absorption par résonance: a) distribution de la densité électronique près de l'avant de la cible; b) réfraction d'un faisceau laser dans un plasma à gradient de densité; c) le champ électrique dans le plasma

Ainsi, le laser brille sur notre plasma sous un angle, eh bien, qu'il soit à 45 degrés, et en même temps il est polarisé dans le plan d'incidence. La polarisation est indiquée par des flèches rouges sur la figure. Notre plasma a un gradient de densité, ce qui signifie que son indice de réfraction est en constante évolution (ici, il augmente). À un certain point, il arrivera qu'une certaine couche de plasma pour notre laser deviendra «rotative» et elle réfléchira, c'est-à-dire qu'elle se propagera pendant un certain temps parallèlement à la couche critique. Il est important de noter qu'il tournera avant qu'il n'atteigne la couche de densité critique, puisque nous l'avons lancé à un angle par rapport à la normale. La densité de plasma à laquelle le faisceau laser tourne est donnée par cette équation:

$$ afficher $$ n_t = n_c \ cos ^ 2 \ alpha, $$ afficher $$

où

$ inline $ n_c $ inline $ Est la densité critique, et

$ inline $ \ alpha $ inline $ - angle d'incidence de la lumière.

Maintenant, le plaisir commence. Rappelons que la lumière n'est pas seulement un flux de photons, mais aussi une onde électromagnétique, c'est-à-dire que notre élan a un champ électrique qui oscille harmonieusement avec une grande amplitude. Lorsque la lumière se propage parallèlement à la couche critique, une onde stationnaire se forme, qui ne change pas avec le temps (naturellement, tant que l'impulsion laser est en place). Le champ de cette onde, en effet, pénètre plus loin que la couche de plasma où la lumière a tourné et atteint la couche critique. Permettez-moi de vous rappeler que la fréquence des oscillations du plasma dans la couche critique est la même que la fréquence du rayonnement laser, ce qui signifie que la résonance se produit. Lorsque le laser a cessé de briller, l'énergie qu'il a communiquée aux électrons de la couche critique est distribuée par les chocs aux autres électrons, ce qui signifie que le plasma est chauffé.

Alors, où est en fait l'accélération?

Maintenant que nous avons réchauffé les électrons dans le puits de plasma et que le laser ne brille plus, nous pouvons dire comment les protons sont accélérés. Pour ce faire, regardez les photos ci-dessous. Jusqu'à présent, je n'ai jamais dit d'où venaient les protons. Naturellement, ils n'apparaissent pas à partir des noyaux du matériau en feuille. Comme nous ne sommes pas très soignés et ne portons pas de gants (les mains transpirent fortement), l'eau et les hydrocarbures sont à la surface du film. L'hydrogène ionisé est notre source inestimable de protons. Vérifié: si vous supprimez la pollution, il n'y aura pas de protons.

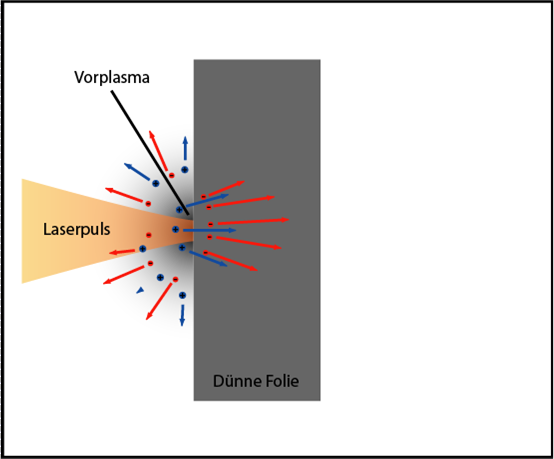	La formation de plasma par un piédestal, c'est-à-dire l'ionisation de l'avant de la cible. En tant que cible, une feuille d'une épaisseur de 0,4 à 12 microns est généralement utilisée.
	Ici, la partie principale de l'impulsion interagit avec le plasma créé et le chauffe. Certains électrons se sont tellement bien réchauffés qu'ils s'envolent de l'arrière de la cible.
	Lorsque de nombreux électrons s'envolent, la charge positive restante dans la feuille les retire. Dans le plasma, ils chauffent à nouveau et s'envolent. Pendant un certain temps, un équilibre dynamique est établi. Le champ électrique est dirigé perpendiculairement à la cible
	Ce champ très électrique détache les protons et autres ions (selon ce qu'il y avait du tout) de la surface arrière de la cible, puis les accélère. Au moment où les ions se sont accélérés, le nuage d'électrons se désagrège déjà et toutes les particules commencent à voler plus loin ensemble. Et puis on commence à croire qu'ils n'interagissent plus.

Diviser et conquérir

Pour le moment, la position est la suivante: le laser ne brille pas depuis longtemps, il y a un trou dans la feuille, les protons avec des électrons volent amicalement de la cible normalement vers sa surface arrière. Nous n'avons pas du tout besoin d'électrons, c'est pourquoi un aimant vient à notre aide. Lorsqu'un faisceau de particules chargées vole à travers un champ magnétique, les forces de Lorentz de chaque particule sont déviées proportionnellement à sa vitesse et à sa charge. En conséquence, les protons et les électrons vont dévier dans des directions différentes, et nous ne regarderons tout simplement pas dans la direction des électrons. Soit dit en passant, plus l'énergie du proton (c'est-à-dire sa vitesse) est grande, moins il s'écartera. Cela signifie qu'en plaçant un écran sensible aux protons, nous pouvons voir les énergies des protons accélérés. Quelques comparaisons supplémentaires en nombre: un aimant qui nous accompagne en permanence et crée un champ d'environ 0,75 T; dans les appareils d'IRM, le champ magnétique est de 1,5 à 3 T.

De plus, nous pouvons voir le profil d'un faisceau de protons volants. C'est rond, au fait. Et si nous pouvons également mesurer l'énergie du proton dans chaque partie du faisceau, nous pouvons restaurer uniquement la forme du nuage d'électrons, qui a accéléré nos protons.

Au lieu d'une conclusion

Une question juste peut se poser, pourquoi tout cela est nécessaire. Ma réponse préférée est juste comme ça.Il s'agit d'une science fondamentale, et essayer de trouver ses applications momentanées est inutile. Peut-être que dans quelques années, il trouvera son application dans le traitement du cancer ou de la fusion thermonucléaire, mais pour l'instant la tâche principale est d'apprendre quelque chose de nouveau sur le monde qui nous entoure, juste comme ça, car c'est intéressant.

Pour ceux qui sont particulièrement curieux du laser lui-même et de son appareil

Comme promis, je parlerai ici du laser, avec l'aide duquel je fais de la science. J'ai déjà mentionné certaines caractéristiques de notre laser, mais je n'ai pas parlé du taux de répétition des impulsions. Elle est d'environ 80 MHz. Cette fréquence est déterminée uniquement par la longueur du résonateur et l'inverse du temps pendant lequel la lumière parvient à voler dans les deux sens à travers le résonateur. Pour l’avenir, je dirai qu’il n’est pas pratique d’amplifier des impulsions à une telle fréquence, c’est incroyablement difficile du point de vue technique et vous ne pouvez pas économiser de l’électricité.

Je n'entrerai pas spécialement dans la théorie du laser. Les bases de l'origine du rayonnement laser sont parfaitement exposées dans un article de Wikipedia sur l'émission stimulée. Si vous essayez d'être très bref, alors trois composants sont nécessaires pour le rayonnement laser: le milieu actif (les photons volent également hors de lui), le pompage (il maintient le milieu actif dans un état dans lequel il y a plus d'atomes excités qui peuvent émettre), et aussi un résonateur ( il garantit que les photons se copient lors de plusieurs passages à travers le milieu actif). Si vous assemblez tous les composants et priez, le laser commencera à briller, mais en continu. Si vous réessayez, vous pouvez lui faire générer des impulsions, y compris celles aussi courtes que sur mon installation. Pour les plus curieux,La méthode de génération d'impulsions femtosecondes est appelée verrouillage en mode passif. Et maintenant une petite caractéristique d'impulsions bien, très courtes. On pense souvent que le laser brille à la même longueur d'onde, et en mode continu, ainsi qu'à de longues impulsions, cela peut même être appelé vrai. En fait, en raison d'un certain nombre de processus physiques complexes, que nous ne discuterons certainement pas ici, la forme temporelle de l'impulsion et son spectre sont liés par la transformée de Fourier. C'est-à-dire que plus l'impulsion est courte, plus son spectre est large.la forme temporelle de l'impulsion et son spectre sont liés par la transformée de Fourier. C'est-à-dire que plus l'impulsion est courte, plus son spectre est large.la forme temporelle de l'impulsion et son spectre sont liés par la transformée de Fourier. C'est-à-dire que plus l'impulsion est courte, plus son spectre est large.

Supposons que nous ayons lancé un oscillateur maître, mais l'énergie de ses impulsions est de plusieurs nJ. Rappelez-vous, au début, j'ai dit que l'énergie dans une impulsion qui arrive à une cible est d'environ 2 J? C'est donc un milliard de fois plus. Cela signifie que l'élan doit être renforcé, et nous en parlerons plus en détail.

Les impulsions courtes sont généralement caractérisées par de très grandes puissances de crête (rappelez-vous, partager l'énergie par le temps?), Et cela a un certain nombre de complications. Si le milieu est éclairé par un rayonnement de haute intensité (puissance par unité de surface), il brûlera et si le milieu actif est brûlé, alors rien ne sera amplifié. C'est pourquoi nous choisissons un taux de répétition de 10 Hz et nous les amplifions uniquement. Puisqu'il y a beaucoup d'équipement et que tout cela fonctionne à une telle fréquence, nous avons une boîte spéciale qui distribue ces 10 Hz à tout le fer, et pour chaque appareil, vous pouvez choisir le retard de réception du signal avec une précision de quelques picosecondes.

Il existe deux façons de gérer une intensité élevée. Comme vous pouvez facilement le deviner à partir de sa définition, vous devez soit augmenter la zone, soit réduire la puissance. Avec le premier, tout est très clair, mais la deuxième méthode a été une percée dans la technologie laser au XXe siècle. Si l'impulsion est initialement très courte, elle peut être étirée, renforcée, puis compressée à nouveau.

Pour comprendre comment procéder, nous nous tournons vers les bases de l'optique. Pour différentes longueurs d'onde, les indices de réfraction dans le milieu sont différents, ce qui signifie (par la définition de l'indice de réfraction, soit dit en passant) qu'avec une augmentation de l'indice de réfraction, la vitesse de propagation de la lumière dans le milieu diminue. Et donc nous avons lancé notre impulsion mercredi, et sa partie rouge a traversé le matériau plus rapidement que la bleue, c'est-à-dire que l'impulsion est devenue plus longue et sa puissance de pointe a chuté. Hourra, maintenant rien ne brûle! Pour des connaissances plus approfondies dans ce domaine, je recommande de googler et de lire sur l'amplification des impulsions chirpées (aka Chirped Pulse Amplification ou CPA).

Il ne nous reste plus qu'à augmenter l'élan, compresser, focaliser et l'envoyer pour faire un trou dans le foil!

Et maintenant quelques photos avec légendes.