👨🏽‍🚒 👩‍⚖️ 🛡️ Comment fonctionne le champ de Higgs: 3) comment la particule de Higgs apparaît 📲 🙂 👨🏽‍🏫

Comment fonctionne le champ Higgs:

Dans un article précédent, j'ai décrit comment et pourquoi le champ Higgs n'a pas une valeur moyenne de zéro. Maintenant, je veux décrire ce qu'est une particule de Higgs et comment sa masse résulte des équations.

Je tiens à vous rappeler que si le contraire n'est pas mentionné, je décris toujours la forme la plus simple possible du champ et de la particule de Higgs - la soi-disant Modèle standard de Higgs. Des formes plus complexes sont également possibles; par exemple, plusieurs champs Higgs peuvent exister simultanément, au lieu d'un. Je décrirai peut-être un cas plus complexe dans l'un des articles suivants.

Fig. 1: un champ de classe 1 fluctue dans le temps autour d'une valeur stable Z (x, t) = 0

Dans le dernier article, je n'ai pas insisté sur ce fait, mais parmi les champs élémentaires que nous avons découverts dans la nature, le champ de Higgs est unique. Tous les champs, à l'exception de Higgs, satisfont aux équations de mouvement de classe 0 ou 1. En fait (bien que ce ne soit probablement pas le cas pour tous les champs dans la nature), tous les champs que nous connaissons qui satisfont aux équations de classe 1 le font parce que le champ de Higgs est différent de zéro . Si elle était nulle, elles satisferaient toutes les équations de la classe 0 (comme je l'ai expliqué dans le premier article). Au lieu de cela, le champ Higgs satisfait une équation qui peut être appelée une équation de classe -1.

Pour le champ Z (x, t), les classes que j'ai définies ressemblent à ceci:

d^{2} Z / d t^{2} - c^{2} d^{2} Z / d x^{2} = - B^{2} Z q u a d [C l a s s e 1 - m a s s i f p a r t i c u l e s] d^{2} Z / d t^{2} - c^{2} d^{2} Z / d x^{2} = 0 q u a d [C l a s s e 0 - s a n s m a s s e p a r t i c u l e s] d^{2} Z / d t^{2} - c^{2} d^{2} Z / d x^{2} = + B^{2} Z q u a d [C l a s s e - 1 - i n s t a b l e]

$d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = - B ^ 2 Z \ quad [Classe 1 - massif \; particules] \\ d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = 0 \ quad [Classe 0 - sans masse \; particules] \\ d ^ 2Z / dt ^ 2 - c ^ 2 d ^ 2Z / dx ^ 2 = + B ^ 2 Z \ quad [Classe -1 - instable]$

Les équations impliquent que B ² > 0.

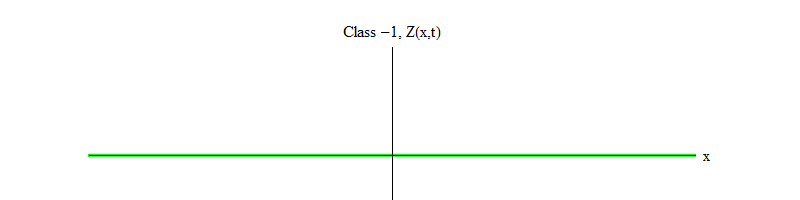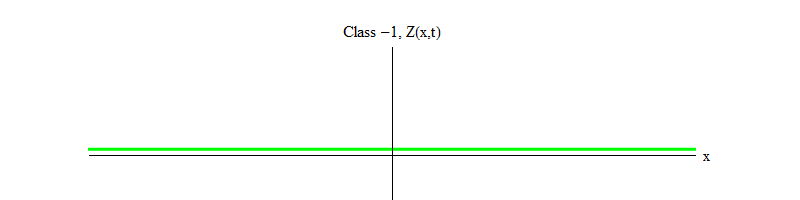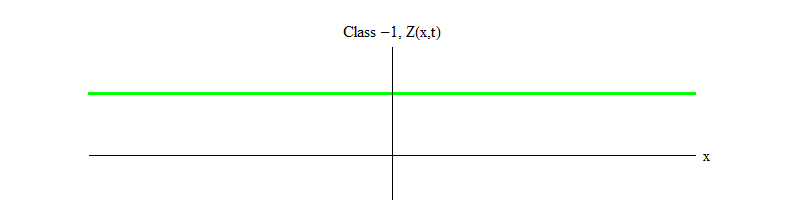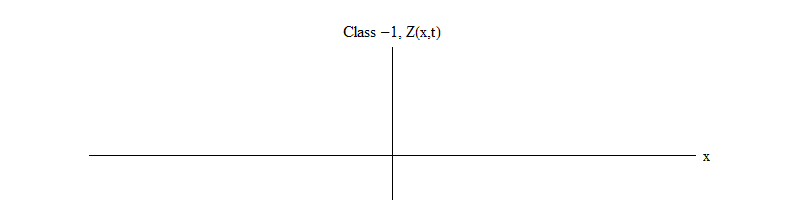Fig. 2: Un champ de classe -1 laisse l'équilibre instable Z (x, t) = 0.

Le signe moins entre la classe 1 et la classe -1 est très important. Dans les deux cas, les solutions des équations contiennent Z (x, t) = 0 comme l'un des cas spéciaux, mais pour la classe 1, Z (x, t) = 0 est stable, c'est-à-dire que Z (x, t) peut fluctuer autour de zéro; ce sont des ondes au comportement décent avec un quantum massif. Et vice versa, la classe -1 Z (x, t) = 0 est instable, c'est-à-dire que Z (x, t) ne fluctuera pas, mais atteindra de plus en plus de valeurs. Si vous ne modifiez pas l'équation, l'amplitude du champ volera à l'infini. Plus précisément, si la solution de l'équation de la classe 1 est l'oscillation Z, comme dans la Fig. 1, la solution à une équation de classe -1 est une croissance exponentielle de Z, comme dans la Fig. 2.

Pour le champ de Higgs, ainsi que pour tout champ existant dans la nature, l'équation de la classe -1 est modifiée à l'aide de termes qui limitent la croissance exponentielle et empêchent le champ d'aller à l'infini. Comme nous l'avons vu dans l'article précédent, le champ de Higgs obéit à l'équation du mouvement

d^{2} H / d t^{2} - c^{2} d^{2} H / d x^{2} = - b^{2} H (H^{2} - v^{2}) = + (b v)^{2} H - b^{2} H^{3}

$d ^ 2H / dt ^ 2 - c ^ 2 d ^ 2H / dx ^ 2 = - b ^ 2 H (H ^ 2 - v ^ 2) = + (bv) ^ 2 H - b ^ 2 H ^ 3$

Il appartient à la classe -1 lorsque H est presque nul, mais il a un membre important de H ³ . Ici b est un nombre positif, et v est la position d'équilibre pour H. Cette équation garantit que si le champ H commence au point H = 0 et passe de la position d'équilibre instable à H positif, alors il oscillera autour de la position d'équilibre stable dans H = v (fig.3).

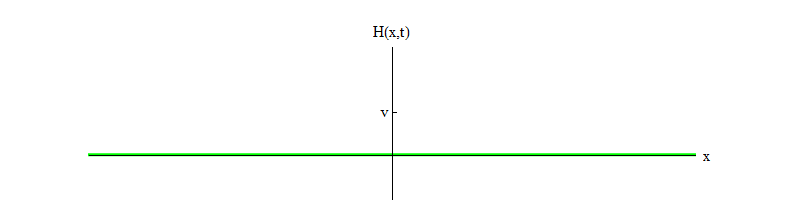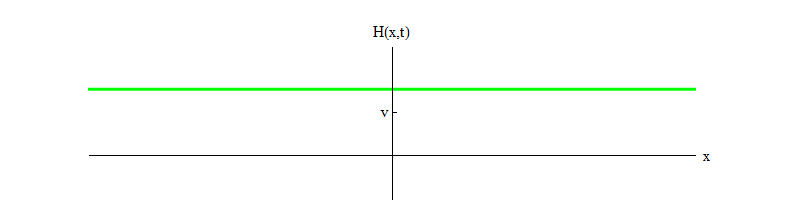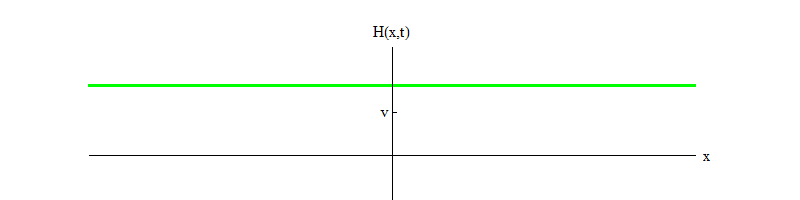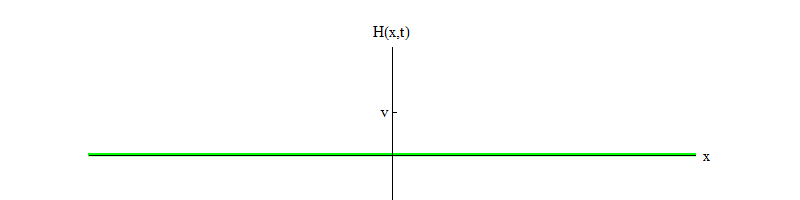Fig. 3

Au fil du temps, les oscillations s'estomperont, en raison des termes de l'équation du mouvement, que j'ai omis par souci de concision; ils permettent à une partie de l'énergie des oscillations du champ H d'être transférée aux ondes d'autres champs (ce sont les mêmes termes non linéaires qui permettent aux particules de Higgs de se désintégrer ). Au fil du temps (Fig. 4), le champ H se calmera dans la position H = v.

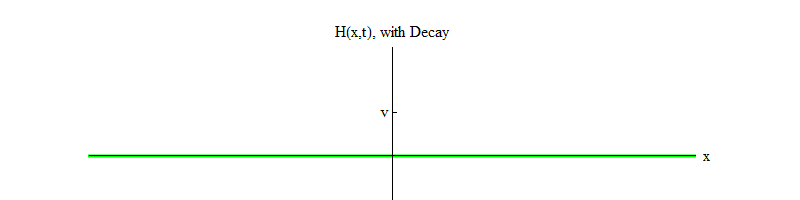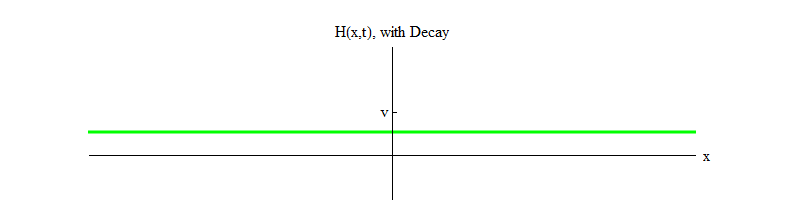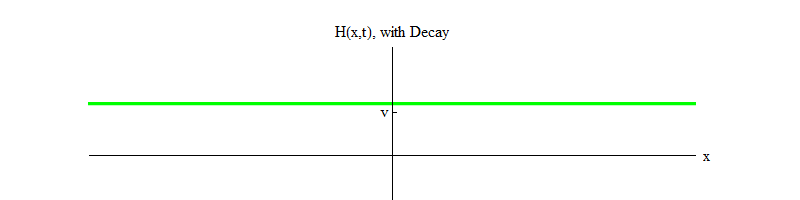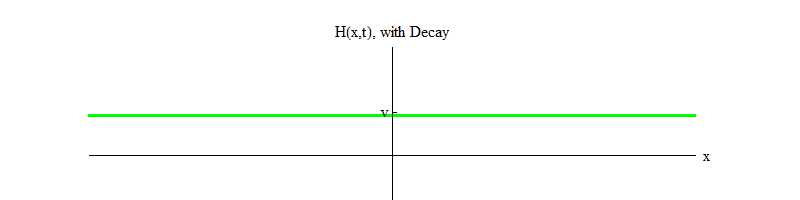Fig. 4

Si un processus physique fait tomber le champ de la position H = v dans une petite région de l'espace, le champ émettra des ondes de la forme

H = v + A c o s [2 p i (n u t - x / l a m b d a)]

$H = v + A cos [2 \ pi (\ nu t - x / \ lambda)]$

Où A est l'amplitude de l'onde, ν et λ est sa fréquence et sa longueur d'onde, et la relation entre ν et λ dépend de la forme exacte de l'équation du mouvement, en particulier, de b et v. Et les quanta de ces ondes seront les particules de Higgs. Question par million: quelle est la masse de la particule de Higgs? Pour calculer cela, nous devons, comme cela est toujours nécessaire pour les particules (représentant les quanta d'onde dans les champs relativistes), déterminer la relation entre la fréquence ν et la longueur d'onde λ des ondes du champ correspondant, puis multiplier le résultat par la constante de Planck h pour obtenir le rapport entre l'énergie et le moment quantique de ces ondes, qui nous dira la masse du quantum (c'est-à-dire les particules).

C'est exactement ce que nous faisons avec le champ S (x, t) mentionné dans le premier article . Nous écrivons une version décalée du champ de Higgs, l'exprimant comme H (x, t) = v + h (x, t) , et la substituons dans l'équation de mouvement du champ H. h (x, t) J'écrirai en gras pour le distinguer de la constante de Planck h. Dans l'exemple du champ S donné dans l'article de revue, une simple équation de mouvement est indiquée, donc le décalage n'a pas changé la masse de la particule S. Mais dans ce cas ce n'est pas le cas! L'équation de mouvement du champ de Higgs est plus complexe, donc l'équation pour h est très différente de l'équation d'origine pour H:

d^{2} t e x t b f h / d t^{2} - c^{2} d^{2} t e x t b f h / d x^{2} = - b^{2} (v + t e x t b f h) (2 v t e x t b f h + t e x t b f h^{2})

$d ^ 2 \ textbf {h} / dt ^ 2 - c ^ 2 d ^ 2 \ textbf {h} / dx ^ 2 = - b ^ 2 (v + \ textbf {h}) (2 v \ textbf {h} + \ textbf {h} ^ 2)$

Où j'ai utilisé le fait que v est une constante et est indépendante de l'espace et du temps. Ensuite, nous rappelons que le quantum du champ de Higgs a une petite amplitude, par conséquent, lorsque nous étudions la seule particule de Higgs (qui est exactement ce dont nous avons besoin pour déterminer sa masse), nous pouvons rejeter tous les termes proportionnels à h ² et h ³ :

d^{2} t e x t b f h / d t^{2} - c^{2} d^{2} t e x t b f h / d x^{2} = - 2 b^{2} v^{2} t e x t b f h + . . .

$d ^ 2 \ textbf {h} / dt ^ 2 - c ^ 2 d ^ 2 \ textbf {h} / dx ^ 2 = - 2 b ^ 2 v ^ 2 \ textbf {h} + ...$

Où "+ ..." rappelle les membres abandonnés. Notez que cette équation pour h (x, t) appartient à la classe 1, bien que nous ayons commencé avec une équation de classe -1 pour H (x, t); cela est dû au fait que H (x, t) était instable dans la région de H = 0, et h (x, t) était stable dans la région de h = 0, où H = v. On peut donc calculer la masse m _{h de} la particule de Higgs h en utilisant la forme suivante d'une équation de classe 1:

m_{h} = s q r t 2 (h / 2 p i) b v / c^{2}

$m_h = \ sqrt2 (h / 2 \ pi) b v / c ^ 2$

h sur le côté droit indique la constante de Planck. Si la particule de type Higgs récemment trouvée sur le LHC s'avère réellement être la particule de Higgs du modèle standard, alors pour la première fois nous pouvons découvrir ce qu'est b (rappelez-vous que v nous le savions déjà il y a très longtemps) et, enfin, nous pouvons trouver la valeur a = b v.

v = 246 GeV;
m _h ≈ 125 GeV / c² (si la nouvelle particule est Higgs)
b ≈ 0,35 (2 π / h) (si la nouvelle particule est le Higgs du modèle standard)
a = bv ≈ 87 GeV (2 π / h) (si la nouvelle particule est le Higgs du modèle standard)

où h, encore une fois, est la constante de Planck. Et les trois dernières quantités ne nous étaient pas connues jusqu'à la récente découverte de la particule de Higgs.

Maintenant, s'il s'avère que le modèle standard ne correspond pas à la nature (si, en plus de H (x, t), il est nécessaire d'ajouter des champs supplémentaires aux champs connus pour expliquer les propriétés d'une particule de masse récemment découverte 125 GeV / c²) - disons si cette particule est l'une de plusieurs types de particules de Higgs - alors nous devrons faire face à cette situation difficile sur le LHC pendant encore quelques années. Vous pouvez imaginer de nombreuses possibilités, et cela n'a aucun sens de vous les expliquer à tous, mais en gros j'en ai décrit certaines ici; et si les données reçues au LHC nous montrent une certaine direction, je vais tout vous expliquer en détail.

Comment fonctionne le champ de Higgs: 3) comment la particule de Higgs apparaît

More articles: