La mécanique classique est intuitive: elle est utilisée quotidiennement et de façon répétée par les gens pour leur survie. Mais jusqu'au XXe siècle, personne n'avait jamais utilisé la mécanique quantique. Elle décrit des choses si petites qu'elles tombent complètement hors de la perception des sens humains. La seule façon de comprendre cette théorie, de jouir de sa beauté, est de bloquer notre intuition avec les mathématiques abstraites.
Leonard Sasskind - un célèbre scientifique américain - vous invite à faire un voyage passionnant au pays de la mécanique quantique. Sur le chemin, vous aurez besoin des connaissances de base du cours de physique de l'école, ainsi que des bases de l'analyse mathématique et de l'algèbre linéaire. Vous devez également savoir quelque chose sur les questions qui ont été abordées dans le premier livre de Susskind sur le «minimum théorique» - «Tout ce que vous devez savoir sur la physique moderne». Mais il est sans crainte si cette connaissance est quelque peu oubliée. Beaucoup d'auteurs rappelleront et expliqueront en cours de route.
La mécanique quantique est une théorie inhabituelle: selon ses postulats, par exemple, nous pouvons tout savoir sur le système et rien sur ses parties individuelles. Einstein et Niels Bohr ont beaucoup discuté de cela et d'autres contradictions. Si vous n'avez pas peur des difficultés, avez un esprit curieux, êtes techniquement compétent, sincèrement et profondément intéressé par la physique, alors ce cours de Leonard Sasskind vous plaira. Le livre se concentre sur les principes logiques de la théorie quantique et ne vise pas à atténuer le paradoxe de la logique quantique, mais à le mettre à la lumière du jour et à essayer de traiter les questions difficiles qu'elle soulève.
Présentation de la fonction Wave
Dans cette conférence, nous utiliserons le langage des fonctions d'onde, nous allons donc faire un bref examen du matériel avant de plonger. Nous avons discuté dans la leçon 5 les fonctions d'onde des objets abstraits, sans expliquer comment elles se rapportent aux ondes ou aux fonctions. Avant de combler cette lacune, je vous rappelle ce dont nous avons discuté précédemment.
Pour commencer, nous choisissons un L observable avec des valeurs propres l et des vecteurs propres | l〉. Soit | Y〉 un vecteur d'état. Puisque les vecteurs propres de l'opérateur hermitien forment une base orthonormée complète, le vecteur | Y〉 peut être développé dans cette base:
Comme vous vous en souvenez des sections 5.1.2 et 5.1.3, les quantités Y (l) sont appelées la fonction d'onde du système. Mais notez: la forme spécifique de Y (l) dépend du L observable spécifique que nous avons initialement sélectionné. Si nous choisissons un autre observable, la fonction d'onde (avec les vecteurs de base et les valeurs propres) se révélera différente, malgré le fait que nous parlons toujours du même état. Par conséquent, nous devons faire une réserve que Y (l) est la fonction d'onde associée à | Yñ. Pour être précis, nous devons dire que Y (l) est la fonction d'onde dans la base L. Si nous utilisons les propriétés d'orthonormalité de cette base de vecteurs 〈li | lj〉 = dij, alors la fonction d'onde dans cette base L peut également être définie en utilisant les produits internes (ou projections) du vecteur d'état | Y〉 sur les vecteurs propres | l〉: Y (l ) = 〈L | Y〉
Il y a deux façons de penser à la fonction d'onde. Tout d'abord, il s'agit d'un ensemble de composants du vecteur d'état dans une base spécifique. Ces composants peuvent être écrits sous la forme d'un vecteur colonne:
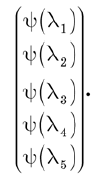
Une autre façon de penser la fonction d'onde est de la considérer comme une fonction de l. Si vous définissez une valeur valide de l, la fonction Y (l) donne un nombre complexe. Ainsi, nous pouvons dire que Y (l) est une fonction à valeur complexe de la variable discrète l. Avec cette considération, les opérateurs linéaires deviennent des opérations qui s'appliquent aux fonctions et donnent de nouvelles fonctions.
Et encore un dernier rappel: la probabilité que l'expérience donne le résultat l est égale à P (l) = Y * (l) Y (l).
Fonctions et vecteurs
Jusqu'à présent, les systèmes que nous avons étudiés avaient des vecteurs d'état de dimension finie. Par exemple, un spin simple est décrit par un espace d'états à deux dimensions. Pour cette raison, les observables n'avaient qu'un nombre fini de valeurs observables possibles. Mais il existe des observables plus complexes qui peuvent avoir un nombre infini de valeurs. Un exemple est une particule. Les coordonnées des particules sont observables, mais contrairement au spin, les coordonnées ont un nombre infini de valeurs possibles. Par exemple, une particule se déplaçant le long de l'axe x peut se trouver à n'importe quel repère de matériau x. En d'autres termes, x est une variable infinie continue. Lorsque les systèmes observés sont continus, la fonction d'onde devient une fonction à part entière de la variable continue. Pour appliquer la mécanique quantique à des systèmes de ce type, nous devons élargir le concept de vecteurs afin d'y inclure des fonctions.
Les fonctions sont des fonctions et les vecteurs sont des vecteurs; ils semblent être des entités complètement différentes, alors dans quel sens les fonctions sont-elles des vecteurs? Si vous considérez les vecteurs comme des flèches dans l'espace tridimensionnel, alors bien sûr, ils ne sont pas du tout les mêmes que des fonctions. Mais si vous regardez les vecteurs de manière plus large, comme les objets mathématiques satisfaisant certains postulats, les fonctions forment en fait un espace vectoriel. Un tel espace vectoriel est souvent appelé un espace de Hilbert en l'honneur du mathématicien David Hilbert.
Considérons l'ensemble des fonctions complexes Y (x) d'une variable réelle x. Par fonction complexe, je veux dire qu'à chaque x il associe un nombre complexe Y (x). La variable indépendante x, en revanche, est une variable réelle ordinaire. Il peut prendre n'importe quelle valeur réelle de –∞ à + ∞.
Maintenant, nous disons exactement ce que nous voulons dire en disant que «les fonctions sont des vecteurs». Ce n'est pas une analogie ou une métaphore superficielle. Sous certaines restrictions (auxquelles nous reviendrons plus loin), des fonctions telles que Y (x) satisfont les axiomes mathématiques qui définissent un espace vectoriel. Nous avons brièvement mentionné cette idée dans la section 1.9.2, et maintenant nous l'utilisons pleinement. En regardant les axiomes d'un espace vectoriel complexe (dans la section 1.9.1), nous voyons que les fonctions complexes les satisfont toutes.
1. La somme de deux fonctions quelconques est une fonction.
2. L'addition de fonctions est commutative.
3. L'ajout de fonctions est associatif.
4. Il existe une fonction zéro unique telle que lorsqu'elle est ajoutée à une fonction, la même fonction est obtenue.
5. Pour toute fonction Y (x) donnée, il existe une fonction unique –Y (x) telle que Y (x) + (–Y (x)) = 0.
6. La multiplication d'une fonction par un nombre complexe donne une fonction et est linéaire.
7. La propriété de distribution est observée, ce qui signifie que
z [Y (x) + j (x)] = zY (x) + zj (x),
[z + w] Y (x) = zY (x) + wY (x),
où z et w sont des nombres complexes.
Tout cela implique que nous pouvons identifier la fonction Y (x) avec le vecteur ket | Y〉 dans l'espace vectoriel abstrait. Il n'est pas surprenant que l'on puisse également définir des vecteurs de soutien-gorge. Le vecteur soutien-gorge 〈Y | correspondant au chum sal | Y〉 est identifié par la fonction conjuguée complexe Y * (x).
Pour utiliser cette idée efficacement, nous devons généraliser certains objets de notre ensemble d'outils mathématiques. Dans les conférences précédentes, les étiquettes qui identifiaient les fonctions d'onde étaient des membres d'un ensemble discret fini, par exemple, les valeurs propres d'un certain observable. Mais maintenant, la variable indépendante est continue. Entre autres choses, cela signifie que nous ne pouvons pas le résumer en utilisant des montants ordinaires. Je pense que tu sais quoi faire. Voici des substituts orientés fonction pour nos trois concepts vectoriels, dont deux que vous connaissez déjà.
• Les montants sont remplacés par des intégrales.
• Les probabilités sont remplacées par des densités de probabilité.
• Le symbole delta Kronecker est remplacé par la fonction delta Dirac.
Examinons de plus près ces outils.
Les montants sont remplacés par des intégrales . Si nous voulions vraiment maintenir la rigueur, nous commencerions par remplacer l'axe x par un ensemble discret de points séparés par de très petits intervalles ε, puis passer à la limite ε → 0. Il faudrait plusieurs pages pour justifier chaque étape. Mais nous pouvons éviter ce problème avec quelques définitions intuitives, telles que le remplacement de sommes par des intégrales. Schématiquement, cette approche peut s'écrire comme suit:
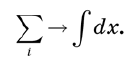
Par exemple, si vous devez calculer l'aire sous la courbe, l'axe x est divisé en petits segments, puis les aires d'un grand nombre de rectangles sont additionnées, tout comme dans une analyse mathématique élémentaire. Lorsque nous laissons les segments se contracter à la taille zéro, la somme devient une intégrale.
Considérons l'accolade 〈Y | et ket | Y〉 et définissent leur produit intérieur. La manière évidente de le faire est de remplacer la somme de l'équation (1.2) par l'intégration. Nous définissons le produit intérieur comme suit:
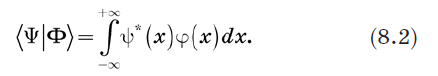Les probabilités sont remplacées par des densités de probabilité . Ensuite, nous identifions P (x) = Y * (x) Y (x) avec la densité de probabilité pour la variable x. Pourquoi avec une densité de probabilité, et pas seulement avec une probabilité? Si x est une variable continue, la probabilité qu'elle prenne une valeur donnée exactement est généralement nulle. Par conséquent, il est plus correct de poser la question de cette façon: quelle est la probabilité que x se situe entre deux valeurs x = a et x = b? La densité de probabilité est déterminée de sorte que cette probabilité soit donnée par l'intégrale
Puisque la probabilité totale doit être 1, nous pouvons définir la normalisation du vecteur comme
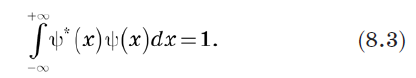Le symbole delta de Kronecker est remplacé par la fonction delta de Dirac . Jusqu'à présent, tout était très familier. La fonction Dirac Delta est quelque chose de nouveau. La fonction delta est un analogue du symbole delta de Kronecker dij, qui par définition est 0 si i ≠ j, et 1 si i = j. Mais il peut être défini d'une autre manière. Considérons tout vecteur Fi dans un espace de dimension finie. Il est facile de voir que le symbole delta de Kronecker satisfait à la condition
Cela est dû au fait que seuls les termes avec j = i sont différents de cette somme. Pendant la sommation, le symbole Kronecker filtre tous les composants de F à l'exception de Fi. Une généralisation évidente de ceci sera de définir une nouvelle fonction qui a la même propriété de filtrage lorsqu'elle est utilisée sous l'intégrale. En d'autres termes, nous avons besoin d'une nouvelle entité d (x - x '), qui a la propriété que pour toute fonction F (x)
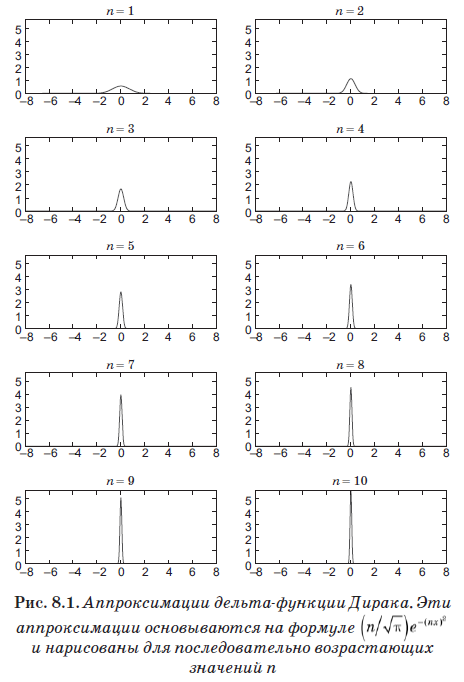
L'équation (8.4) définit une nouvelle entité appelée la fonction delta de Dirac, qui s'est avérée être l'outil le plus important en mécanique quantique. Mais malgré son nom, ce n'est pas vraiment une fonction au sens habituel. Il est égal à zéro où x ≠ x ', mais quand x = x' il va à l'infini. En fait, il est juste infini juste assez pour que l'aire sous d (x) soit égale à 1. En gros, cette fonction est non nulle sur l'intervalle infiniment petit ε, mais sur cet intervalle elle a la valeur 1 / ε. Ainsi, l'aire sous elle est égale à 1 et, plus important encore, elle satisfait l'équation (8.4). Fonction
se rapproche assez bien de la fonction delta pour de très grandes valeurs de n. Dans la fig. 8.1 montre cette optimisation avec des valeurs croissantes de n. Malgré le fait que nous nous sommes installés sur n = 10, c'est-à-dire une très petite valeur, notons que le graphique est déjà devenu un pic très étroit et net.
»Plus d'informations sur le livre sont disponibles sur
le site Web de l'éditeur»
Contenu»
ExtraitPour les lecteurs de ce blog, une remise de 20% sur le coupon -
Sasskind