Le livre «Minimum théorique. Tout ce que vous devez savoir sur la physique moderne »

«Minimum théorique» est un livre pour ceux qui ont manqué des cours de physique à l'école et à l'institut, mais le regrettent déjà. Vous voulez comprendre les bases des sciences naturelles et apprendre à penser et à raisonner comme le font les physiciens modernes? Sous une forme originale et non standard, les célèbres scientifiques américains Leonard Sasskind et George Grabowski offrent un cours d'introduction aux mathématiques et à la physique pour les esprits curieux.

Contrairement à d'autres livres de science populaire qui tentent d'expliquer les lois de la physique d'une manière accessible, en évitant habilement les équations et les formules, les auteurs enseignent au lecteur les fondements classiques des sciences naturelles. Le livre propose sa propre méthodologie d'enseignement originale, complétée par des conférences vidéo publiées sur theoryminimum.com .

Conférence 9. Fluide de phase et théorème de Gibbs - Liouville

Lenny aimait regarder la rivière, surtout pour regarder les petites taches flottant à la surface. Il a essayé d'imaginer comment ils se déplaceraient entre les pierres ou tomberaient dans des tourbillons. Mais le cours de la rivière dans son ensemble - le mouvement combiné d'un grand volume d'eau, avec des ruisseaux qui se séparent, convergent et se dépassent - était au-delà de sa compréhension.

Fluide de phase

Se concentrer sur des conditions initiales spécifiques et suivre une trajectoire séparée dans l'espace des phases est très naturel pour la mécanique classique. Mais il existe également une vision plus large qui couvre toute une famille de trajectoires. Au lieu de placer la pointe du crayon à un certain point dans l'espace des phases et de tracer le seul chemin à partir de là, nous essaierons de faire quelque chose de plus ambitieux. Imaginez que nous ayons un nombre infini de crayons et utilisez-les pour remplir uniformément l'espace des phases de points (par homogénéité, je veux dire que la densité des points en q, p est la même partout). Considérez ces points comme des particules qui composent un fluide imaginaire remplissant l'espace des phases.

Maintenant, laissez chaque point se déplacer selon les équations de mouvement hamiltoniennes:


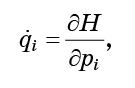
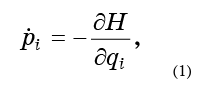
de sorte que notre fluide s'écoule sans fin à travers l'espace de phase.

Un oscillateur harmonique est un bon exemple initial. Dans la leçon 8, nous avons vu que chaque point se déplace sur une orbite circulaire avec une vitesse angulaire constante. (Permettez-moi de vous rappeler que nous parlons de phase plutôt que d'espace de coordonnées. En coordonnées, l'oscillateur se déplace d'avant en arrière dans une dimension.) L'ensemble du fluide dans son ensemble fait un mouvement solide, tournant uniformément autour de l'origine de l'espace de phase.

Revenons maintenant au cas général. Si le nombre de coordonnées est N, alors l'espace de phase et le liquide qu'il contient sont bidimensionnels. Le fluide coule, mais d'une manière très spécifique. Son écoulement a des propriétés particulières. L'un d'eux est que si un point commence par une certaine énergie - c'est-à-dire pour une valeur donnée de H (q, p) - alors il stocke cette valeur d'énergie. Les surfaces d'énergie constante (par exemple, avec une énergie égale à E) sont déterminées par l'équation H (q, p) = E. (2)

Pour chaque valeur de E, nous avons une équation avec 2N variables d'espace de phase qui définit une surface de dimension 2N - 1. En d'autres termes, chaque valeur de E a sa propre surface; lorsque vous passez sur toutes les valeurs E, ces surfaces remplissent tout l'espace des phases. Nous pouvons considérer l'espace de phase avec les surfaces données par l'équation (2) comme une carte de contours (Fig. 1), sur laquelle les horizontales représentent non pas la hauteur, mais les valeurs d'énergie. Si le point liquide se trouve sur une surface spécifique, il y restera pour toujours. C'est la loi de conservation de l'énergie.

L'espace de phase de l'oscillateur harmonique est bidimensionnel et les surfaces d'énergie sont des cercles:

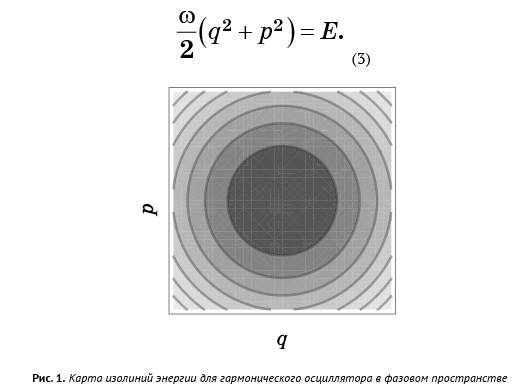
Dans le cas général, les surfaces énergétiques d'un système mécanique sont trop compliquées à visualiser, mais le principe reste le même: les surfaces énergétiques remplissent l'espace de phase sous forme de couches, et le flux se déplace de sorte que les points restent sur la surface sur laquelle ils étaient à l'origine .

Petit rappel

Je voudrais m'arrêter ici et rappeler ce qui a été dit lors de la toute première conférence, où les pièces, les dés et les idées les plus simples sur les lois du mouvement ont été discutées. Nous avons décrit ces lois avec un ensemble de flèches reliant les points qui représentent les états du système. Nous avons également expliqué que les lois sont admissibles et irrecevables, alors que les lois sont réversibles. L'essentiel est que chaque point doit avoir exactement une flèche entrante et exactement une flèche sortante. Si au moins à un moment donné le nombre de flèches entrantes dépasse le nombre de flèches sortantes (c'est ce qu'on appelle la convergence), alors une telle loi est irréversible. Il en va de même dans le cas où il y a plus de flèches sortantes que de flèches entrantes (c'est ce qu'on appelle la divergence). La divergence et la convergence des flèches violent la réversibilité et sont interdites. Jusqu'à présent, nous ne sommes pas revenus sur ce raisonnement. Le moment est venu.

Débit et divergence

Prenons quelques exemples simples d'écoulement de fluide dans un espace ordinaire. Pendant un instant, nous oublions l'espace des phases et considérons simplement un fluide ordinaire se déplaçant dans l'espace tridimensionnel habituel avec des axes notés x, y, z. L'écoulement peut être décrit par le champ de vitesse . Champ de vitesse

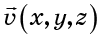
est déterminé en réglant le vecteur vitesse en chaque point de l'espace (Fig. 2).

Vous pouvez également décrire le champ de vitesse avec des composants de vitesse:

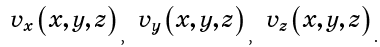
De plus, la vitesse à un moment donné peut dépendre du temps, mais supposons qu'il n'y ait pas une telle dépendance. Dans ce cas, le flux est appelé stationnaire .

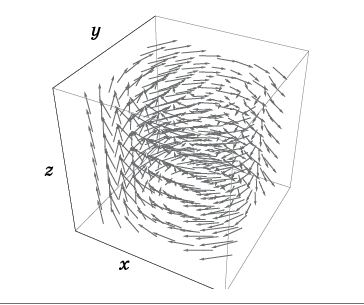
Fig. 2. Champ de vitesse

prend le même montant. Cela signifie également que la densité d'un fluide - le nombre de molécules par unité de volume - est la même partout et est constante dans le temps. Soit dit en passant, le terme "incompressibilité" signifie également inextensibilité. En d'autres termes, le liquide ne peut pas augmenter de volume. Considérons une petite cellule cubique définie par les conditions:

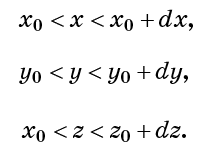
L'incompressibilité implique que le nombre de points fluides dans chacune de ces cellules est constant. Cela signifie également que le débit total de fluide entrant dans la cellule (par unité de temps) doit être nul. (Combien de points du flux entrent, le même nombre sort.) Considérez le nombre de molécules passant par unité de temps à travers la surface cellulaire x = x0. Elle sera proportionnelle à la vitesse d'écoulement sur cette surface vx (x0).

Si la vitesse vx est la même à x0 et à x0 + dx, alors le flux dans la cellule par x = x0 sera le même que le flux qui en sort par x = x0 + dx. Mais si vx change dans toute la cellule, ces deux flux seront déséquilibrés. Le débit total entrant dans la cellule à travers ces deux faces sera proportionnel

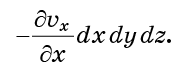
Exactement les mêmes considérations s'appliquent aux faces y0 et y0 + dy, ainsi qu'à z0 et z0 + dz. Si tous sont ajoutés, le flux total de molécules dans la cellule (entrée moins sortie)

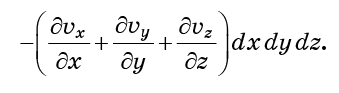
La combinaison des dérivés entre parenthèses est appelée la divergence du champ vectoriel
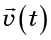
et est désigné

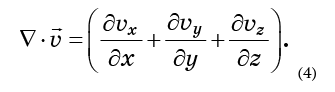
La divergence reflète le degré de dispersion des molécules ou l'augmentation du volume qu'elles occupent. Si le fluide est incompressible, ce volume ne doit pas changer, ce qui signifie que la divergence doit être nulle.

Une façon de comprendre l'incompressibilité est d'imaginer que chaque molécule ou point occupe un volume qui ne peut pas être changé. Ils ne peuvent pas être compressés en un volume plus petit, ils ne disparaissent pas et n'apparaissent pas de nulle part. Avec un peu de réflexion, vous pouvez voir à quel point incompressible et réversible sont similaires. Dans les exemples que nous avons analysés dans la leçon 1, les flèches ont également déterminé une sorte de flux. Et essentiellement, ce flux était incompressible, du moins s'il était réversible. La question naturelle qui en découle est la suivante: l'écoulement dans l'espace des phases est-il réversible? La réponse est oui, si le système satisfait les équations de Hamilton. Et le théorème exprimant cette incompressibilité est appelé le théorème de Liouville.

Théorème de Liouville

Revenons à l'écoulement du fluide dans l'espace des phases et considérons les composantes de la vitesse du fluide à chaque point de l'espace des phases. Il n'est pas besoin de dire que le fluide de phase n'est pas tridimensionnel dans les coordonnées x, y, z. C'est un fluide à deux dimensions dans les coordonnées pi, qi.

Ainsi, il existe 2N composantes du champ de vitesse - une pour chaque coordonnée q et chaque coordonnée p. Laissez-les

Le concept de divergence exprimé par l'équation (4) est facilement généralisé à n'importe quel nombre de dimensions. En trois dimensions, c'est la somme des dérivées des composantes de vitesse dans les directions correspondantes. De la même manière, il est déterminé pour un nombre quelconque de dimensions. Dans le cas de l'espace des phases, la divergence du flux est la somme de 2N membres:

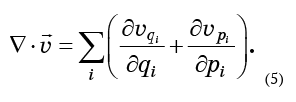
Si le fluide est incompressible, cette expression doit être nulle. Pour le calculer, vous devez connaître les composants du champ de vitesse - ils ne sont bien sûr rien d'autre que les vitesses des particules du fluide de phase.

Le vecteur d'écoulement en un point donné est identifié avec la vitesse d'une particule imaginaire en ce point. En d'autres termes

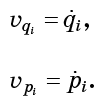
De plus
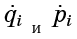
- ce ne sont que les quantités qui entrent dans les équations de Hamilton (1):


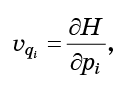
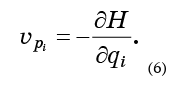
Il suffit de remplacer les équations (6) par la formule (5) et d'obtenir

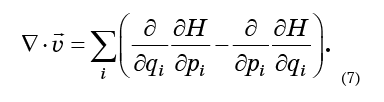
Rappelant que la dérivée seconde de la forme


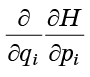
ne dépend pas de l'ordre de différenciation, on comprendra que les termes de l'équation (7) se détruisent exactement deux à deux:


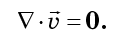
Ainsi, le fluide de phase est incompressible. En mécanique classique, l'incompressibilité d'un fluide de phase s'appelle le théorème de Liouville, bien qu'il n'ait presque aucun rapport avec le mathématicien français Joseph Liouville. Il a été publié pour la première fois en 1903 par le grand physicien américain Josiah Willard Gibbs, et il est également connu sous le nom de théorème de Gibbs - Liouville.

Nous avons déterminé l'incompressibilité d'un fluide en exigeant que la quantité totale de fluide entrant dans une petite cellule soit nulle. Il existe une autre définition strictement équivalente. Imaginez un volume de liquide à un moment donné. Ce volume peut avoir n'importe quelle forme: sphérique, cubique, en forme de goutte - peu importe. Nous allons maintenant suivre le mouvement de tous les points de ce volume. Après un certain temps, une goutte de liquide sera dans un endroit différent et aura une forme différente. Mais si le fluide est incompressible, le volume des gouttelettes restera le même qu'à l'origine. On peut donc reformuler le théorème de Liouville: le volume occupé par une goutte de phase liquide est conservé dans le temps .

Prenons un exemple d'oscillateur harmonique dans lequel un fluide tourne autour d'un point de référence. De toute évidence, la goutte conserve du volume, car tout son mouvement est réduit à une rotation à l'état solide. La forme de la goutte reste inchangée, mais c'est le cas pour l'oscillateur harmonique. Prenons un autre exemple. Supposons que l'hamiltonien ait la forme H = pq.

Peut-être que cela vous semblera différent du hamiltonien, bien que ce soit tout à fait correct. Nous dérivons les équations du mouvement:

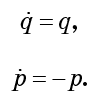
Selon ces équations, q augmente exponentiellement avec le temps, et p diminue exponentiellement avec la même vitesse. En d'autres termes, le flux presse le fluide contre l'axe p, tout en le dilatant simultanément le long de l'axe q dans la même mesure. Toute baisse s'étend le long de q et se contracte le long de p. De toute évidence, la goutte subit d'énormes déformations, mais son volume de phase ne change pas.

Le théorème de Liouville est l'analogue imaginable le plus proche du type d'irréversibilité dont nous avons discuté dans la leçon 1. En mécanique quantique, le théorème de Liouville est remplacé par une version quantique appelée unitarité. L'unitarité est encore plus similaire à ce que nous avons discuté dans la leçon 1, mais c'est le sujet du prochain numéro du Minimum Théorique.

»Plus d'informations sur le livre sont disponibles sur le site Web de l'éditeur
» Exclamation
» Extrait

Pour les lecteurs de ce blog, une remise de 20% sur le coupon - Minimum théorique