Après avoir versé du sable sur une plaque élastique oscillante, on peut voir la formation de figures Hladni . Ils servent souvent d'exemple de la «beauté naturelle» des phénomènes physiques, bien que derrière eux se trouve la physique assez simple de l'excitation résonnante des ondes stationnaires. Et peu de gens prêtent attention à la curieuse caractéristique de ces figures: les lignes sur elles évitent les intersections, comme si une force les repoussait. Essayons de comprendre quel type de physique se cache derrière cette répulsion et comment elle est liée à la théorie quantique du chaos.

Ondes stationnaires

Comme nous le savons, les corps élastiques peuvent produire des vibrations plutôt complexes, au cours desquelles ils se contractent, s'étirent, se plient et se tordent. Néanmoins, les vibrations de tout corps élastique peuvent être représentées comme une combinaison de vibrations normales plus simples superposées les unes aux autres. Voilà à quoi ressemblent plusieurs vibrations normales d'un corps élastique simple - une corde tendue unidimensionnelle.

Chaque vibration normale est représentée par une onde stationnaire qui, contrairement à une onde progressive, reste immobile et a son propre schéma de distribution des amplitudes des oscillations dans l'espace. Sur cette figure, les antinœuds peuvent être distingués - les points où l'amplitude des oscillations atteint les maxima, et les nœuds - les points fixes auxquels l'amplitude des oscillations est nulle. De plus, chacune de ces ondes oscille avec sa propre fréquence . Dans le cas d'une chaîne, comme vous pouvez le voir, la fréquence des oscillations d'une onde stationnaire augmente avec l'augmentation du nombre de nœuds et d'antinœuds.


Examinons maintenant un système bidimensionnel, dont un exemple est une fine membrane élastique tendue sur un cadre rigide. Les vibrations normales d'une membrane ronde semblent plus compliquées que dans le cas d'une chaîne, et au lieu de points-nœuds individuels, il y a des lignes nodales le long desquelles la membrane est stationnaire.


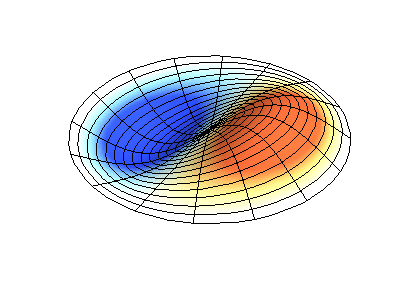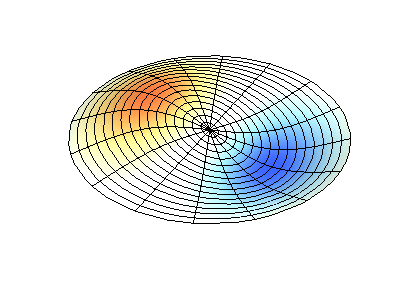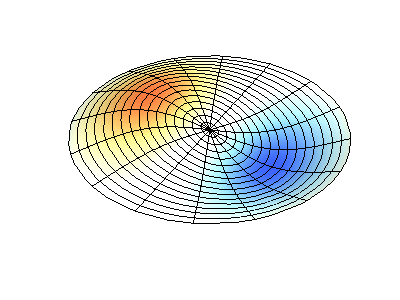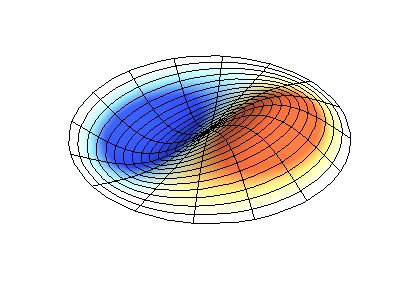
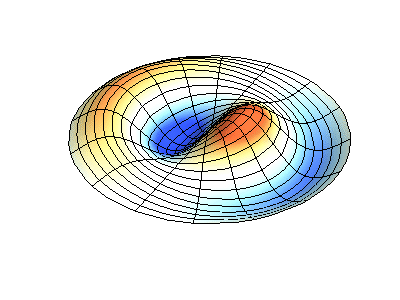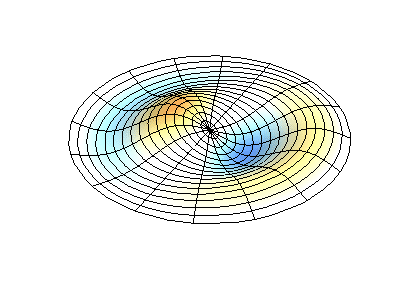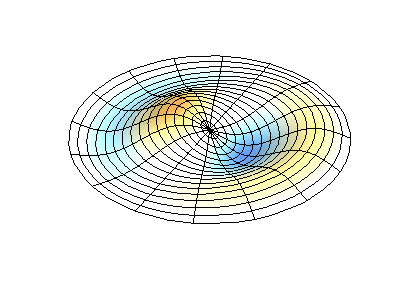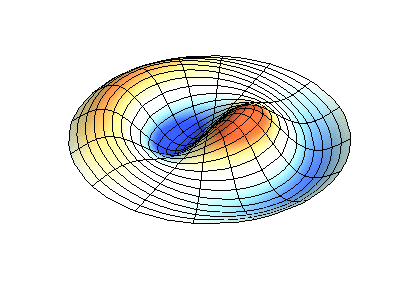
Vibrations normales d'une membrane ronde à bords fixes. Source


La couleur verte montre des lignes nodales.

À une membrane ronde, les lignes nodales, qui sont des cercles et des segments le long des rayons, peuvent se croiser à angle droit. Si les bords de la membrane ont une forme arbitraire, trouver les fréquences de vibrations normales et les motifs de leurs nœuds et antinœuds deviennent un problème qui ne peut être résolu qu'à l'aide d'un ordinateur.

Profils de l'amplitude des oscillations des ondes stationnaires sur les membranes sous la forme d'un carré avec un trou , des flocons de neige Koch et la surface d'un chaton .

Les équations décrivant les oscillations d'une plaque élastique mince diffèrent des équations d'oscillation de la membrane, car la plaque a sa propre rigidité, tandis que la membrane est molle et élastique uniquement en raison de la tension par des forces externes. Cependant, il existe également des ensembles de vibrations normales, dont les dessins dépendent sensiblement de la forme des limites.

Les chiffres de Hladni

Comme mentionné ci-dessus, dans le cas général, les vibrations corporelles sont une combinaison de tout un ensemble de vibrations normales qui y sont excitées. Le phénomène de résonance vous permet d'exciter sélectivement l'une des vibrations normales dont nous avons besoin - pour cela, nous devons balancer le corps en utilisant une force externe avec une fréquence égale à la fréquence naturelle de l'oscillation normale.

Les deux vidéos ci-dessous montrent un schéma typique pour obtenir des figures de Hladni: une plaque élastique est fixée au centre à un générateur de vibrations mécaniques, dont la fréquence augmente progressivement. Les vibrations normales des plaques avec leurs motifs de nœuds et d'antinœuds sont excitées lorsque la fréquence de l'oscillateur correspond de manière résonnante aux fréquences naturelles de ces vibrations (les fréquences naturelles sont affichées dans la vidéo dans le coin inférieur gauche).

Voici la version de la même vidéo dans laquelle les fréquences des vibrations normales peuvent être estimées à l'oreille.

Et voici un peu plus joli.

Nous voyons des motifs de nœuds et d'antinœuds du fait que les courants d'air près d'une plaque oscillante soufflent des grains de sable sur les lignes nodales d'une onde stationnaire ^(*) . Ainsi, les figures de Hladni nous montrent des motifs de lignes nodales de vibrations normales d'une plaque élastique.

Plusieurs figurines Hladni sur le pont supérieur de la guitare. Source

Un autre exemple de vagues normales est les vagues stationnaires à la surface de l'eau. Ils sont décrits par une équation qui diffère des équations d'oscillation des plaques et des membranes, mais suivent les mêmes lois qualitatives, et avec leur aide, il est possible d'obtenir des analogues des figures de Hladni.

Microparticules à la surface de l'eau dans des récipients de formes diverses. La ligne noire montre une échelle de 2 millimètres. Source

Chaos classique

Ainsi, nous avons vu que dans le cas d'une membrane ronde, les lignes nodales sont théoriquement! - se croisent remarquablement, en même temps, sur les figures de Hladni sur des plaques carrées ou plus complexes, les lignes nodales évitent les intersections. Pour comprendre la raison de ces modèles, nous devrons faire une courte excursion dans la théorie du chaos.

Le chaos classique est une propriété des systèmes mécaniques, consistant en une dépendance extrêmement forte de la trajectoire de leur mouvement aux changements des conditions initiales. Cette relation est également connue sous le nom d '« effet papillon ». Un exemple frappant de comportement chaotique peut être trouvé dans les tentatives de prévision du temps: le système d'équations décrivant le mouvement de l'atmosphère et des océans ne permet pas de faire des prévisions suffisamment précises à long terme en raison d'erreurs croissantes de façon exponentielle en raison de petites inexactitudes dans les données initiales ^(**) .

Le phénomène du chaos a été ouvertement et popularisé par le météorologue et mathématicien Edward Lorenz , qui a découvert que deux calculs de prévisions météorologiques commençant par des conditions initiales très proches étaient initialement presque indiscernables, mais à un moment donné, ils ont commencé à diverger radicalement.

Deux calculs d'Edward Lorenz, à partir des valeurs initiales proches 0,506 et 0,506127. Source

Les systèmes les plus simples, sur l'exemple desquels il est commode d'étudier le chaos, sont les billards - des sections d'une surface plane le long desquelles une balle peut rouler sans friction, rebondissant absolument élastique sur des parois rigides. Dans le billard chaotique, les trajectoires de la balle, qui présentent de légères différences au tout début, divergent ensuite considérablement. Un exemple de billard chaotique est le billard du Sinaï illustré ci-dessous, qui est une piscine rectangulaire avec un obstacle circulaire au centre. Comme nous le verrons, c'est précisément à cause de cet obstacle que le billard devient chaotique.

Deux trajectoires de balle exponentiellement divergentes dans le billard du Sinaï. Source

Systèmes intégrables et chaotiques

Les systèmes mécaniques qui ne sont pas chaotiques sont appelés intégrables , et avec l'exemple du billard, vous pouvez clairement voir la différence entre les systèmes intégrables et chaotiques.

Les billards rectangulaires et ronds sont intégrables grâce à leur forme symétrique ^(***) . Le mouvement de la balle dans ces billards est simplement une combinaison de deux mouvements périodiques indépendants. Dans le billard rectangulaire, ce sont des mouvements avec rebonds des murs horizontalement et verticalement, et rondement c'est un mouvement le long du rayon et un mouvement angulaire dans un cercle autour du centre. Un tel mouvement est facilement calculé et ne montre pas de comportement chaotique.

Trajectoires de balle dans les billards intégrables.

Les billards de forme plus complexe, ne possédant pas une symétrie aussi élevée qu'un cercle ou un rectangle, sont chaotiques ^(****) . L'un d'eux que nous avons vu ci-dessus est le billard du Sinaï, dans lequel la symétrie du rectangle est détruite par une inclusion circulaire au centre. Sont également souvent considérés les billards "stade" et les billards en forme d'escargots Pascal. La balle se déplace dans des billards chaotiques sur des chemins très compliqués et ne se décompose pas en mouvements périodiques plus simples.

La trajectoire de la balle dans le billard chaotique "stade" et "escargot Pascal".

Ici, vous pouvez déjà deviner que la présence d'intersections entre les lignes dans les figures de Hladni est déterminée par le fait que la plaque a la forme d'un billard intégrable ou chaotique. Cela se voit clairement sur les photos ci-dessous.

Assiettes rondes Hladni, démontrant les propriétés du billard intégré. Source

Démontrer les propriétés du billard chaotique de la plaque Hladni sous forme de billard «stade», le cas du violon et de la place, dont la symétrie est brisée par un luminaire rond au centre (analogue du billard du Sinaï). Source

Chaos quantique

Comment comprendre pourquoi les intersections entre les lignes nodales sont dues à l'intégrabilité du billard? Pour ce faire, nous devons nous tourner vers la théorie quantique du chaos , combinant la théorie du chaos avec la mécanique des oscillations et des ondes. Si en mécanique classique la balle en billard est décrite comme un point matériel se déplaçant le long d'une certaine trajectoire, alors en mécanique quantique son mouvement est décrit comme la propagation d'une onde obéissant à l'équation de Schrödinger et réfléchie par les parois du billard.

Stades de propagation des ondes dans le billard quantique. Initialement, l'onde est concentrée en une impulsion ronde et se déplace de gauche à droite, puis elle se propage et se reflète à plusieurs reprises sur les murs. Source

La même chose sous forme d'animation, mais avec des conditions initiales légèrement différentes.

Comme dans le cas des vibrations des membranes et des plaques, l'équation de Schrödinger décrivant le billard quantique permet de trouver des vibrations normales sous forme d'ondes stationnaires, qui ont un motif caractéristique de lignes nodales et d'antinœuds, individuel pour chaque oscillation et en fonction de la forme des limites.

Exemples de profils d'amplitudes d'oscillations dans les ondes stationnaires de billard quantique chaotique « escargot de Pascal » et « stade ».

Les modèles d'ondes stationnaires dans les billards quantiques intégrables et chaotiques sont qualitativement différents: les billards intégrables montrent des modèles symétriques et ordonnés d'ondes stationnaires, tandis que dans les billards chaotiques, les modèles d'ondes stationnaires sont très déroutants et ne montrent aucun modèle visible (à la fin de l'article, il sera montré que certains intéressants modèles existent encore).

Les amplitudes d'oscillation dans les ondes stationnaires d'un billard rond intégrable (rangée supérieure) et d'un billard chaotique sous la forme d'un escargot Pascal (rangée inférieure). Source

Les images bizarres de vibrations normales dans un billard chaotique font parfois l'objet d'une étude distincte. Source

Une différence qualitative est également observée dans les modèles de lignes nodales: dans le cas du billard quantique intégrable, nous voyons des familles ordonnées de lignes qui se croisent , et dans le billard chaotique, ces lignes, en règle générale, ne se croisent pas .

Ci-dessus: lignes nodales (lignes noires entre les zones bleues et rouges) de vagues stationnaires de billard intégrable - rond et rectangulaire -. Ci-dessous: les lignes nodales de l'une des ondes stationnaires du billard chaotique - un quart du billard du stade .

Intersection ou non intersection?

Pourquoi les lignes nodales des billards chaotiques ne se croisent-elles pas? En 1976, la mathématicienne Karen Uhlenbeck a prouvé un théorème selon lequel les lignes nodales d'ondes stationnaires de billard quantique, d'une manière générale, ne devraient pas se croiser.

Dans une forme simplifiée, cela peut être montré comme suit: supposons que deux lignes nodales se coupent en un point ( x ₀ , y ₀ ). Pour cela, la fonction f ( x, y ), qui détermine la dépendance de l'amplitude de l'onde stationnaire sur les coordonnées, doit simultanément satisfaire à trois conditions:

1) Il doit être égal à zéro au point ( x ₀ , y ₀ ), car ce point est nodal.
2) Si vous vous déplacez du point ( x ₀ , y ₀ ) dans la direction de la première ligne nodale, alors f ( x, y ) doit rester égal à zéro.
3) Si vous vous déplacez du point ( x ₀ , y ₀ ) dans la direction de la deuxième ligne nodale, alors f ( x, y ) doit également rester égal à zéro.


Au total, nous avons trois conditions (ou trois équations) imposées à la fonction de deux variables f ( x, y ). Comme nous le savons, une équation ne suffit pas pour trouver complètement les deux inconnues x et y , deux équations suffisent déjà pour cela et trois équations, c'est trop. Le système de trois équations pour deux inconnues, d'une manière générale, n'aura pas de solution, à moins que nous ayons la chance. Par conséquent, les points d'intersection des lignes nodales ne peuvent exister qu'à titre d'exception .

Dans le billard intégrable, de telles exceptions surviennent. Comme nous l'avons vu plus haut, leurs propriétés particulières - prévisibilité du mouvement, absence de chaos, régularités régulières des ondes stationnaires - sont le résultat de leur grande symétrie. La même symétrie assure la satisfaction simultanée de trois conditions nécessaires aux intersections de lignes nodales.

Examinons maintenant de plus près des exemples de figures Hladni typiques du billard intégrable et chaotique. La figure ci-dessous montre trois cas caractéristiques . À gauche, la plaque a la forme d'un cercle, de sorte que le billard quantique correspondant est intégrable et que les lignes nodales se croisent. Au centre, la plaque est rectangulaire, ce qui correspond également à un système intégrable, cependant, un montage rond au centre viole légèrement la symétrie du rectangle, de sorte que les lignes nodales ne se croisent pas partout. Un exemple de système purement chaotique est montré à droite: une plaque en forme de quart du billard du Sinaï (dans le coin supérieur droit il y a une découpe circulaire), les lignes nodales sur lesquelles ne se croisent plus.



Ainsi, plus la forme de la plaque - en tenant compte de sa fixation - est différente de la forme d'un billard intégré (comme un cercle ou un rectangle), moins il y a d'intersections de lignes nodales sur celle-ci .

Ce n'est pas si facile d'obtenir de belles figures Hladni avec des lignes qui se croisent sur une assiette ronde. Lors de l'excitation de vibrations avec une fixation centrale, la symétrie circulaire de l'ensemble du système interdit la formation de lignes nodales radiales, nous ne verrons donc qu'un ensemble de cercles ennuyeux (cette difficulté peut être contournée par des vibrations excitantes non pas du centre, mais du bord de la plaque à l'aide de l'archet du violon). Si la plaque est fixée décentrée, les figures de Hladni deviendront plus intéressantes, mais en raison de la violation de la symétrie circulaire, le système cessera d'être intégrable.

Plaque ronde, montage central.

Plaque ronde, montage décalé du centre.

Et voici différentes options avec des plaques rondes et non circulaires.

Enfin, un lecteur attentif peut remarquer: mais je vois que parfois les lignes nodales se croisent même sur des plaques «chaotiques». Comment se fait-il que leur intersection soit interdite par le théorème d'Uhlenbeck?

Premièrement, les lignes nodales peuvent éviter l'intersection, mais avant qu'elles ne soient si proches qu'en raison de la largeur finie du chemin de sable, il nous semblera qu'il y a une intersection. Deuxièmement, entre les systèmes intégrables et chaotiques, en fait, il n'y a pas de frontière nette.

Les lignes nodales - elles séparent les zones noires et blanches - dans le billard quantique intégrable et chaotique (gauche et droite), et dans le cas pseudo-intégrable intermédiaire (au centre). Dans le cas intermédiaire, il y a plusieurs intersections des lignes nodales, alors que dans le cas chaotique il n'y en a pas du tout. Source

Dans la théorie classique du chaos, la célèbre théorie de Kolmogorov-Arnold-Moser est consacrée à cette question. Elle dit que si la symétrie du système intégrable est légèrement violée, il ne présentera pas immédiatement un comportement chaotique, mais, pour la plupart, conservera sa prévisibilité du mouvement. Au niveau de la théorie quantique du chaos et des figures de Hladni, cela se manifeste par le fait qu'à certains endroits les intersections de lignes nodales sont préservées. Cela se produit soit à des points particulièrement symétriques du billard, soit loin de la source de perturbation, ce qui viole la symétrie du système intégrable.

Quoi d'autre?

Quoi d'autre est intéressant dans la théorie quantique du chaos? Pour le lecteur intéressé, je mentionnerai trois questions supplémentaires qui ne sont plus directement liées aux chiffres de Hladni.

1) Un phénomène important étudié par cette théorie est l' universalité des systèmes chaotiques. La grande majorité des systèmes dans lesquels des vibrations normales peuvent se produire sont chaotiques, et tous - quelle que soit leur nature physique! - obéissez aux mêmes lois. Le phénomène d'universalité, dans lequel des systèmes complètement différents sont décrits par les mêmes formules, est lui-même très beau et sert de rappel de l'unité mathématique du monde physique.

Statistiques des distances entre fréquences adjacentes de vibrations normales dans des systèmes chaotiques de nature physique différente, décrites partout par la même formule universelle de Wigner-Dyson. Source

2) Les modèles de vibrations normales des billards chaotiques ont une caractéristique intéressante appelée «cicatrices quantiques» . Nous avons vu que les trajectoires de la balle dans un billard chaotique semblent généralement très déroutantes. Mais il y a des exceptions - ce sont des orbites périodiques , des trajectoires fermées assez simples et courtes le long desquelles la balle fait un mouvement périodique. Les cicatrices quantiques sont appelées épaississement marqué des ondes stationnaires le long des orbites périodiques.

Cicatrices quantiques dans le "stade" de billard, courant le long des orbites périodiques indiquées par des lignes rouges et vertes. Source

3) Jusqu'à présent, nous avons parlé de systèmes bidimensionnels. Si nous considérons la propagation des ondes dans l'espace tridimensionnel, des lignes nodales peuvent également apparaître ici le long desquelles l'amplitude d'oscillation est nulle. Ceci est particulièrement important lors de l'étude de la condensation et de la superfluidité de Bose, où des milliers d'atomes se déplacent comme de simples " ondes de matière ". Une analyse de la structure des lignes nodales des ondes de matière dans l'espace tridimensionnel est nécessaire, par exemple, pour comprendre comment la turbulence quantique apparaît et se développe dans les systèmes superfluides.

Structures tridimensionnelles enchevêtrées de lignes nodales d '«ondes de matière» stationnaires dans le condensat de Bose. Source .

^(*) Si la taille des particules versées sur la plaque est suffisamment petite, elles seront soufflées non pas aux nœuds, mais aux antinœuds de l'onde stationnaire, comme cela a été montré dans ce travail expérimental .

^(**) «» «» , : – , , . .

^(***) – . , , , .

^(****) , – . , . – .